☆ Bonus - Convolutions From Scratch

Learning Objectives

• Understand how array strides work, and why they're important for efficient linear operations
• Learn how to use as_strided to perform simple linear operations like trace and matrix multiplication
• Implement your own convolutions and maxpooling functions using stride-based methods

This section is designed to get you familiar with the implementational details of layers like Linear and Conv2d. You'll be using libraries like einops, and functions like torch.as_strided to get a very low-level picture of how these operations work, which will help build up your overall understanding.

Note that torch.as_strided isn't something which will come up explicitly in much of the rest of the course (unlike einops). The purpose of the stride exercises is more to give you an appreciation for what's going on under the hood, so that we can build layers of abstraction on top of that during the rest of this week (and by extension this course). I see this as analogous to how many CS courses start by teaching you about languages like C and concepts like pointers and memory management before moving on to higher-level langauges like Python which abstract away these details. The hope is that when you get to the later sections of the course, you'll have the tools to understand them better.

Reading

• Python NumPy, 6.1 - as_strided() explains what array strides are.
• as_strided and sum are all you need gives an overview of how to use as_strided to perform array operations.
• Advanced NumPy: Master stride tricks with 25 illustrated exercises provides several clear and intuitive examples of as_strided being used to construct arrays.

Basic stride exercises

Array strides, and the as_strided method, are important to understand well because lots of linear operations are actually implementing something like as_strided under the hood.

Run the following code, to define this tensor:

test_input = t.tensor(
    [
        [0, 1, 2, 3, 4],
        [5, 6, 7, 8, 9],
        [10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19],
    ],
    dtype=t.float,
)

This tensor is stored in a contiguous block in computer memory.

We can call the stride method to get the strides of this particular array. Running test_input.stride(), we get (5, 1). This means that we need to skip over one element in the storage of this tensor to get to the next element in the row, and 5 elements to get the next element in the column (because you have to jump over all 5 elements in the row). Another way of phrasing this: the nth element in the stride is the number of elements we need to skip over to move one index position in the nth dimension.

Exercise - fill in the correct size and stride

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to ~30 minutes on these exercises collectively. Strides can be confusing and fiddly, so you should be willing to look at the solution if you're stuck! They are not the most important part of the material today. ```

In the exercises below, we will work with the test_input tensor above. You should fill in the size and stride arguments so that calling test_input.as_strided with these arguments produces the desired output. When you run the cell, the for loop at the end will iterate through the test cases and print out whether the test passed or failed.

We've already filled in the first two as an example, along with illustrations explaining what's going on:

By the end of these examples, hopefully you'll have a clear idea of what's going on. If you're still confused by some of these, then the dropdown below the codeblock contains some annotations to explain the answers.

TestCase = namedtuple("TestCase", ["output", "size", "stride"])

test_cases = [
    # Example 1
    TestCase(
        output=t.tensor([0, 1, 2, 3]),
        size=(4,),
        stride=(1,),
    ),
    # Example 2
    TestCase(
        output=t.tensor([[0, 2], [5, 7]]),
        size=(2, 2),
        stride=(5, 2),
    ),
    # Start of exercises (you should fill in size & stride for all 6 of these):
    TestCase(
        output=t.tensor([0, 1, 2, 3, 4]),
        size=None,
        stride=None,
    ),
    TestCase(
        output=t.tensor([0, 5, 10, 15]),
        size=None,
        stride=None,
    ),
    TestCase(
        output=t.tensor([[0, 1, 2], [5, 6, 7]]),
        size=None,
        stride=None,
    ),
    TestCase(
        output=t.tensor([[0, 1, 2], [10, 11, 12]]),
        size=None,
        stride=None,
    ),
    TestCase(
        output=t.tensor([[0, 0, 0], [11, 11, 11]]),
        size=None,
        stride=None,
    ),
    TestCase(
        output=t.tensor([0, 6, 12, 18]),
        size=None,
        stride=None,
    ),
]


for i, test_case in enumerate(test_cases):
    if (test_case.size is None) or (test_case.stride is None):
        print(f"Test {i} failed: attempt missing.")
    else:
        actual = test_input.as_strided(size=test_case.size, stride=test_case.stride)
        if (test_case.output != actual).any():
            print(f"Test {i} failed\n  Expected: {test_case.output}\n  Actual: {actual}")
        else:
            print(f"Test {i} passed!")

test_cases = [
    # Example 1
    TestCase(
        output=t.tensor([0, 1, 2, 3]),
        size=(4,),
        stride=(1,),
    ),
    # Example 2
    TestCase(
        output=t.tensor([[0, 2], [5, 7]]),
        size=(2, 2),
        stride=(5, 2),
    ),
    # Start of exercises (you should fill in size & stride for all 6 of these):
    TestCase(
        output=t.tensor([0, 1, 2, 3, 4]),
        size=(5,),
        stride=(1,),
    ),
    # # Explanation: the tensor is held in a contiguous memory block. When you get to the end of one
    # # row, a single stride jumps to the start of the next row.
    #
    TestCase(
        output=t.tensor([0, 5, 10, 15]),
        size=(4,),
        stride=(5,),
    ),
    # # Explanation: this is same as previous case, only now you're moving in colspace (i.e.
    # # skipping 5 elements) each time you move one element across the output tensor. So stride is 5
    # # rather than 1.
    #
    TestCase(
        output=t.tensor([[0, 1, 2], [5, 6, 7]]),
        size=(2, 3),
        stride=(5, 1),
    ),
    # # Explanation: as you move one column to the right in the output tensor, you want to jump one
    # # element in test_input (since you're just going one column to the right). As you move one
    # # row down in the output tensor, you want to jump down one row in test_input (which is
    # # equivalent to a stride of 5, because we're jumping 5 elements).
    #
    TestCase(
        output=t.tensor([[0, 1, 2], [10, 11, 12]]),
        size=(2, 3),
        stride=(10, 1),
    ),
    # # Explanation: same as previous, except now we're jumping over 10 elements (2 rows of 5
    # # elements) each time we move down in the output tensor.
    #
    TestCase(
        output=t.tensor([[0, 0, 0], [11, 11, 11]]),
        size=(2, 3),
        stride=(11, 0),
    ),
    # # Explanation: we're copying horizontally, i.e. we don't move in the original tensor when we
    # # step right in the output tensor, so the stride is 0 (this is a very important case to
    # # understand for the later exercises, since it's effectively our way of doing an einops.repeat
    # # operation!). As we move one row down, we're jumping over 11 elements in the original tensor
    # # (going from 0 to 11).
    #
    TestCase(
        output=t.tensor([0, 6, 12, 18]),
        size=(4,),
        stride=(6,),
    ),
    # Explanation: we're effectively taking the diagonal elements of the original tensor here,
    # since we're creating a 1D tensor with stride equal to (row_stride + col_stride) of the
    # original tensor.
]

Intermediate stride exercises

Now that you're comfortable with the basics, we'll dive a little deeper with as_strided. In the last few exercises of this section, you'll start to implement some more challenging stride functions: trace, matrix-vector and matrix-matrix multiplication, just like we did for einsum in the previous section.

Exercise - trace

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 10-15 minutes on this exercise. Use the hint if you're stuck. ```

You might find the very last example in the previous section helpful for this exercise.

def as_strided_trace(mat: Float[Tensor, "i j"]) -> Float[Tensor, ""]:
    """
    Returns the same as `torch.trace`, using only `as_strided` and `sum` methods.
    """
    raise NotImplementedError()


tests.test_trace(as_strided_trace)

def as_strided_trace(mat: Float[Tensor, "i j"]) -> Float[Tensor, ""]:
    """
    Returns the same as torch.trace, using only as_strided and sum methods.
    """
    stride = mat.stride()
assert len(stride) == 2, f"matrix should be 2D, not {len(stride)}"
    assert mat.size(0) == mat.size(1), "matrix should be square"
diag = mat.as_strided((mat.size(0),), (stride[0] + stride[1],))
return diag.sum()

Exercise - matrix-vector multiplication

```yaml Difficulty: 🔴🔴🔴⚪⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 15-20 minutes on this exercise. The hints should be especially useful here if you're stuck. There are two hints available to you. ```

You should implement this using only as_strided and sum methods, and elementwise multiplication * - in other words, no matrix multiplication functions!

You might find the second last example in the previous section helpful for this exercise (i.e. the one that involved a stride of zero).

def as_strided_mv(mat: Float[Tensor, "i j"], vec: Float[Tensor, "j"]) -> Float[Tensor, "i"]:
    """
    Returns the same as `torch.matmul`, using only `as_strided` and `sum` methods.
    """
    raise NotImplementedError()


tests.test_mv(as_strided_mv)
tests.test_mv2(as_strided_mv)

def as_strided_mv(mat: Float[Tensor, "i j"], vec: Float[Tensor, "j"]) -> Float[Tensor, "i"]:
    """
    Returns the same as torch.matmul, using only as_strided and sum methods.
    """
    sizeM = mat.shape
    sizeV = vec.shape
    strideV = vec.stride()
assert len(sizeM) == 2, f"mat1 should be 2D, not {len(sizeM)}"
    assert sizeM[1] == sizeV[0], (
        f"mat{list(sizeM)}, vec{list(sizeV)} not compatible for multiplication"
    )
vec_expanded = vec.as_strided(mat.shape, (0, strideV[0]))
return (mat * vec_expanded).sum(dim=1)

Exercise - matrix-matrix multiplication

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 15-25 minutes on this exercise. The hints should be especially useful here if you're stuck. There are two hints available to you. ```

Like the previous function, this should only involve as_strided, sum, and pointwise multiplication.

def as_strided_mm(matA: Float[Tensor, "i j"], matB: Float[Tensor, "j k"]) -> Float[Tensor, "i k"]:
    """
    Returns the same as `torch.matmul`, using only `as_strided` and `sum` methods.
    """
    raise NotImplementedError()


tests.test_mm(as_strided_mm)
tests.test_mm2(as_strided_mm)

def as_strided_mm(matA: Float[Tensor, "i j"], matB: Float[Tensor, "j k"]) -> Float[Tensor, "i k"]:
    """
    Returns the same as torch.matmul, using only as_strided and sum methods.
    """
    assert len(matA.shape) == 2, f"mat1 should be 2D, not {len(matA.shape)}"
    assert len(matB.shape) == 2, f"mat2 should be 2D, not {len(matB.shape)}"
    assert matA.shape[1] == matB.shape[0], (
        f"mat1{list(matA.shape)}, mat2{list(matB.shape)} not compatible for multiplication"
    )
# Get the matrix strides, and matrix dims
    sA0, sA1 = matA.stride()
    dA0, dA1 = matA.shape
    sB0, sB1 = matB.stride()
    _, dB1 = matB.shape
# Get target size for matrices, as well as the strides necessary to create them
    expanded_size = (dA0, dA1, dB1)
    matA_expanded_stride = (sA0, sA1, 0)
    matB_expanded_stride = (0, sB0, sB1)
# Create the strided matrices, and return their product summed over middle dimension
    matA_expanded = matA.as_strided(expanded_size, matA_expanded_stride)
    matB_expanded = matB.as_strided(expanded_size, matB_expanded_stride)
    return (matA_expanded * matB_expanded).sum(dim=1)

conv1d minimal

Here, we will implement the PyTorch conv1d function, which can be found here. We will start with a simple implementation where stride=1 and padding=0, with the other arguments set to their default values.

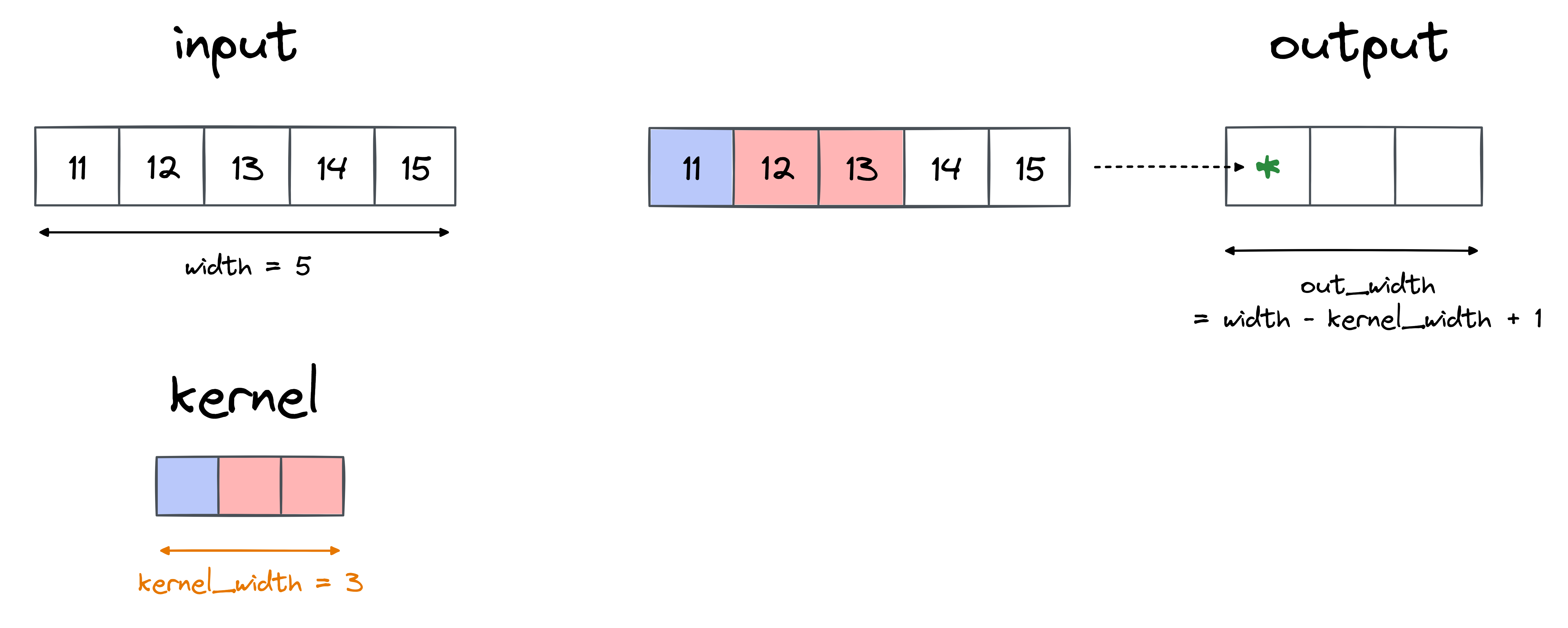
Firstly, some explanation of conv1d in PyTorch. The 1 in 1d here refers to the number of dimensions along which we slide the weights (also called the kernel) when we convolve. Importantly, it does not refer to the number of dimensions of the tensors that are being used in our calculations. Typically the input and kernel are both 3D:

• input.shape = (batch, in_channels, width)
• kernel.shape = (out_channels, in_channels, kernel_width)

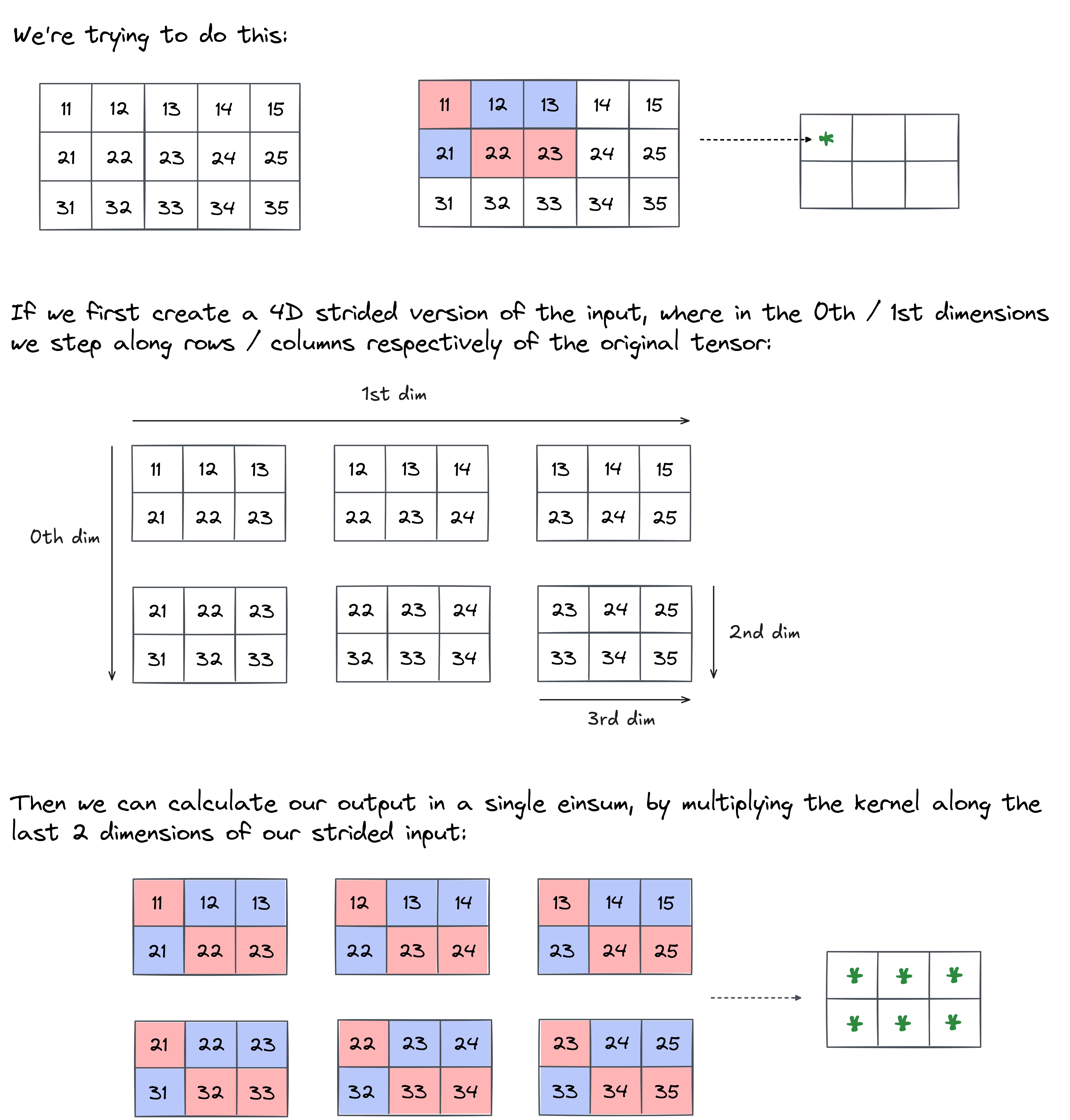
A typical convolution operation is illustrated in the sketch below. Some notes on this sketch:

• The kernel_width dimension of the kernel slides along the width dimension of the input. The output_width of the output is determined by the number of kernels that can be fit inside it; the formula can be seen in the right part of the sketch.
• For each possible position of the kernel inside the model (i.e. each freezeframe position in the sketch), the operation happening is as follows:
  • We take the product of the kernel values with the corresponding input values, and then take the sum
  • This gives us a single value for each output channel
  • These values are then passed into the output tensor
• The sketch assumes a batch size of 1. To generalise to a larger batch number, we can just imagine this operation being repeated identically on every input.

A note on out_channels

The out_channels in a conv2d layer denotes the number of filters the layer uses. Each filter detects specific features in the input, producing an output with as many channels as filters.

This number isn't tied to the input image's channels but is a design choice in the neural network architecture. Commonly, powers of 2 are chosen for computational efficiency, and deeper layers might have more channels to capture complex features. Additionally, this parameter is sometimes chosen based on the heuristic of wanting to balance the parameter count / compute for each layer - which is why you often see out_channels growing as the size of each feature map gets smaller.

Exercise - implement minimal 1D conv (part 1)

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 15-25 minutes on this exercise. Use the diagram in the dropdown below, if you're stuck. ```

Below, you should implement conv1d_minimal. This is a function which works just like conv1d, but takes the default stride and padding values (these will be added back in later). You are allowed to use as_strided and einsum.

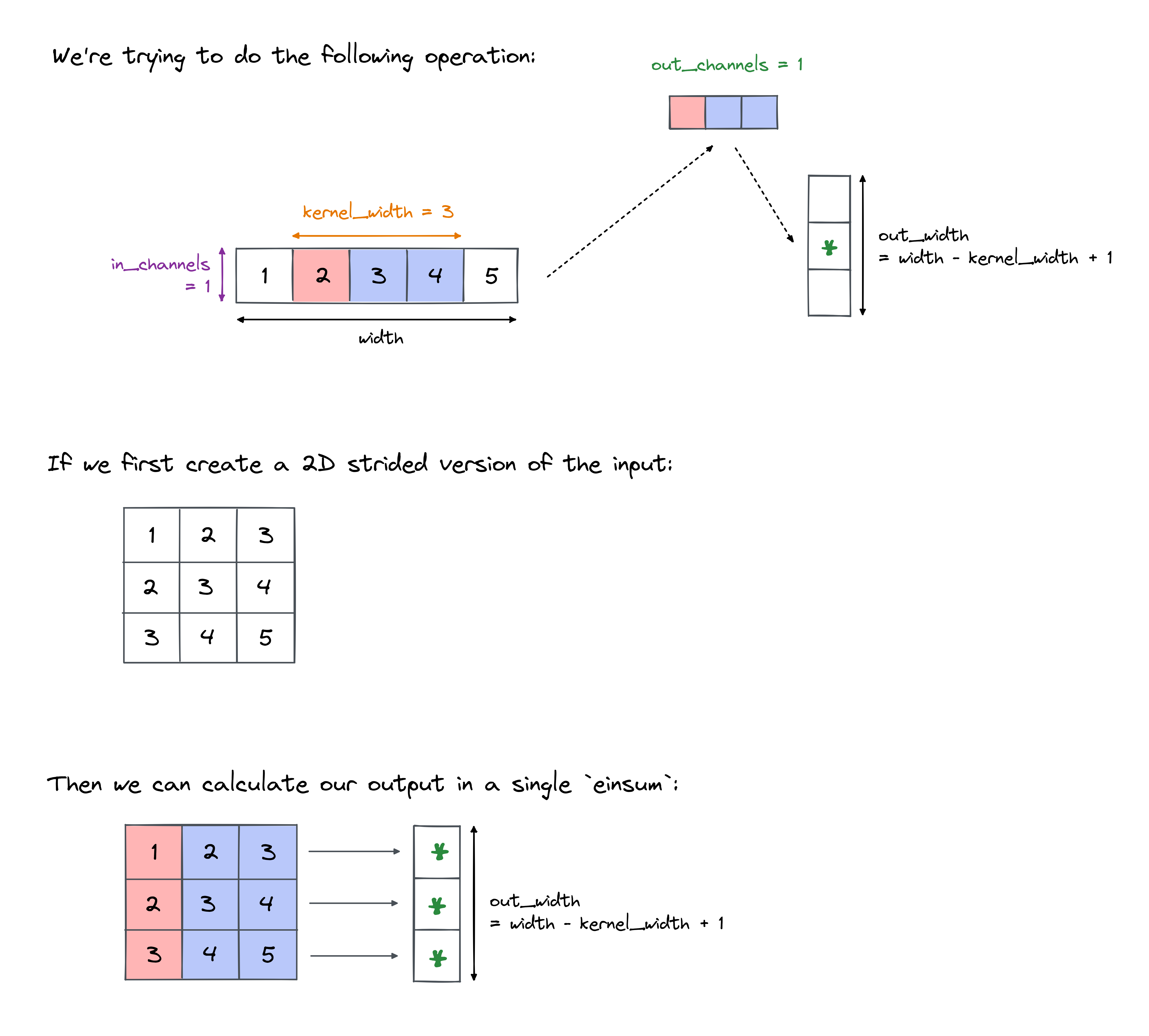
Because this is a difficult exercise, we've given you a "simplified" function to implement first. This gets rid of the batch dimension, and input & output channel dimensions, so you only have to think about x and weights being one-dimensional tensors:

def conv1d_minimal_simple(
    x: Float[Tensor, "width"], weights: Float[Tensor, "kernel_width"]
) -> Float[Tensor, "output_width"]:
    """
    Like torch's conv1d using bias=False and all other keyword arguments left at default values.

    Simplifications: batch = input channels = output channels = 1.
    """
    raise NotImplementedError()


tests.test_conv1d_minimal_simple(conv1d_minimal_simple)

If you're stuck on conv1d_minimal_simple, click here to see a diagram which should help.

This diagram illustrates the striding operation you'll need to perform on x. Once you do this, it's just a matter of using the right einsum operation to get the output.

def conv1d_minimal_simple(
    x: Float[Tensor, "width"], weights: Float[Tensor, "kernel_width"]
) -> Float[Tensor, "output_width"]:
    """
    Like torch's conv1d using bias=False and all other keyword arguments left at default values.
    Simplifications: batch = input channels = output channels = 1.
    """
    # Get output width, using formula
    w = x.shape[0]
    kw = weights.shape[0]
    ow = w - kw + 1
# Get strides for x
    s_w = x.stride(0)
# Get strided x (the new dimension has same stride as the original stride of x)
    x_new_shape = (ow, kw)
    x_new_stride = (s_w, s_w)
    # Common error: s_w is always 1 if the tensor x wasn't itself created via striding, so if you
    # put 1 here you won't spot your mistake until you try this with conv2d!
    x_strided = x.as_strided(size=x_new_shape, stride=x_new_stride)
return einops.einsum(x_strided, weights, "ow kw, kw -> ow")

Exercise - implement minimal 1D conv (part 2)

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 15-25 minutes on this exercise. ```

Once you've implemented this function, you should now adapt it to make a "full version", which includes batch, in_channel and out_channel dimensions. If you're stuck, the dropdowns provide hints for how each of these new dimensions should be handled.

def conv1d_minimal(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "out_channels in_channels kernel_width"],
) -> Float[Tensor, "batch out_channels output_width"]:
    """
    Like torch's conv1d using bias=False and all other keyword arguments left at default values.
    """
    raise NotImplementedError()


tests.test_conv1d_minimal(conv1d_minimal)

def conv1d_minimal(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "out_channels in_channels kernel_width"],
) -> Float[Tensor, "batch out_channels output_width"]:
    """
    Like torch's conv1d using bias=False and all other keyword arguments left at default values.
    """
    b, ic, w = x.shape
    oc, ic2, kw = weights.shape
    assert ic == ic2, "in_channels for x and weights don't match up"
    # Get output width, using formula
    ow = w - kw + 1
# Get strides for x
    s_b, s_ic, s_w = x.stride()
# Get strided x (the new dimension has the same stride as the original width-stride of x)
    x_new_shape = (b, ic, ow, kw)
    x_new_stride = (s_b, s_ic, s_w, s_w)
    # Common error: xsWi is always 1, so if you put 1 here you won't spot your mistake until you try
    # this with conv2d!
    x_strided = x.as_strided(size=x_new_shape, stride=x_new_stride)
return einops.einsum(x_strided, weights, "b ic ow kw, oc ic kw -> b oc ow")

conv2d minimal

2D convolutions are conceptually similar to 1D. The only difference is in how you move the kernel across the tensor as you take your convolution. In this case, you will be moving the tensor across two dimensions:

For this reason, 1D convolutions tend to be used for signals (e.g. audio), 2D convolutions are used for images, and 3D convolutions are used for 3D scans (e.g. in medical applications).

Exercise - implement 2D minimal convolutions

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 20-25 minutes on this exercise. Use the diagram in the dropdown below, if you're stuck. ```

You should implement conv2d in a similar way to conv1d. Again, this is expected to be difficult and there are several hints you can go through. We've also provided a diagram to help you, like for the 1D case:

def conv2d_minimal(
    x: Float[Tensor, "batch in_channels height width"],
    weights: Float[Tensor, "out_channels in_channels kernel_height kernel_width"],
) -> Float[Tensor, "batch out_channels height_padding width_padding"]:
    """
    Like torch's conv2d using bias=False and all other keyword arguments left at default values.
    """
    raise NotImplementedError()


tests.test_conv2d_minimal(conv2d_minimal)

Hint & diagram

You should be doing the same thing that you did for the 1D version. The only difference is that you're introducing 2 new dimensions to your strided version of x, rather than 1 (their sizes should be output_height and output_width, and their strides should be the same as the original height and width strides of x respectively).

def conv2d_minimal(
    x: Float[Tensor, "batch in_channels height width"],
    weights: Float[Tensor, "out_channels in_channels kernel_height kernel_width"],
) -> Float[Tensor, "batch out_channels height_padding width_padding"]:
    """
    Like torch's conv2d using bias=False and all other keyword arguments left at default values.
    """
    b, ic, h, w = x.shape
    oc, ic2, kh, kw = weights.shape
    assert ic == ic2, "in_channels for x and weights don't match up"
    ow = w - kw + 1
    oh = h - kh + 1
s_b, s_ic, s_h, s_w = x.stride()
# Get strided x (the new height/width dims have the same stride as the original
    # height/width-strides of x)
    x_new_shape = (b, ic, oh, ow, kh, kw)
    x_new_stride = (s_b, s_ic, s_h, s_w, s_h, s_w)
x_strided = x.as_strided(size=x_new_shape, stride=x_new_stride)
return einops.einsum(x_strided, weights, "b ic oh ow kh kw, oc ic kh kw -> b oc oh ow")

Padding

For a full version of conv, and for maxpool (which will follow shortly), you'll need to implement pad helper functions. PyTorch has some very generic padding functions, but to keep things simple and build up gradually, we'll write 1D and 2D functions individually.

Exercise - implement padding

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 15-20 minutes on this exercise, and the next. ```

The pad1d function applies padding to the width dimension of a 1D tensor, i.e. we pad with left entries to the start of the last dimension of x and with right entries to the end of the last dimension of x.

Tips: * Use the new_full method of the input tensor. This is a clean way to ensure that the output tensor is on the same device as the input, and has the same dtype. * You can use three dots to denote slicing over multiple dimensions. For instance, x[..., 0] will take the 0th slice of x along its last dimension. This is equivalent to x[:, 0] for 2D, x[:, :, 0] for 3D, etc.

def pad1d(
    x: Float[Tensor, "batch in_channels width"], left: int, right: int, pad_value: float
) -> Float[Tensor, "batch in_channels width_padding"]:
    """Return a new tensor with padding applied to the edges."""
    raise NotImplementedError()


tests.test_pad1d(pad1d)
tests.test_pad1d_multi_channel(pad1d)

def pad1d(
    x: Float[Tensor, "batch in_channels width"], left: int, right: int, pad_value: float
) -> Float[Tensor, "batch in_channels width_padding"]:
    """Return a new tensor with padding applied to the edges."""
    B, C, W = x.shape
    output = x.new_full(size=(B, C, left + W + right), fill_value=pad_value)
    output[..., left : left + W] = (
        x  # note we can't use left:-right, because right might be zero
    )
    return output

Once you've passed the tests, you can implement the 2D version. The left and right padding arguments apply to the width dimension, and the top and bottom padding arguments apply to the height dimension.

def pad2d(
    x: Float[Tensor, "batch in_channels height width"],
    left: int,
    right: int,
    top: int,
    bottom: int,
    pad_value: float,
) -> Float[Tensor, "batch in_channels height_padding width_padding"]:
    """Return a new tensor with padding applied to the width & height dimensions."""
    raise NotImplementedError()


tests.test_pad2d(pad2d)
tests.test_pad2d_multi_channel(pad2d)

def pad2d(
    x: Float[Tensor, "batch in_channels height width"],
    left: int,
    right: int,
    top: int,
    bottom: int,
    pad_value: float,
) -> Float[Tensor, "batch in_channels height_padding width_padding"]:
    """Return a new tensor with padding applied to the width & height dimensions."""
    B, C, H, W = x.shape
    output = x.new_full(size=(B, C, top + H + bottom, left + W + right), fill_value=pad_value)
    output[..., top : top + H, left : left + W] = x
    return output

Full convolutions

Now, you'll extend conv1d to handle the stride and padding arguments.

stride is the number of input positions that the kernel slides at each step. padding is the number of zeros concatenated to each side of the input before the convolution.

Output shape should be (batch, output_channels, output_length), where output_length can be calculated as follows:

Verify for yourself that the forumla above simplifies to the formula we used earlier when padding is 0 and stride is 1.

Docs for pytorch's conv1d can be found here.

Exercise - implement 1D convolutions

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 20-25 minutes on this exercise. ```

def conv1d(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "out_channels in_channels kernel_width"],
    stride: int = 1,
    padding: int = 0,
) -> Float[Tensor, "batch out_channels width"]:
    """
    Like torch's conv1d using bias=False.
    """
    raise NotImplementedError()


tests.test_conv1d(conv1d)

Hint - dealing with strides

The following diagram shows how you should create the strided version of x differently, if you have a stride of 2 rather than the default stride of 1.

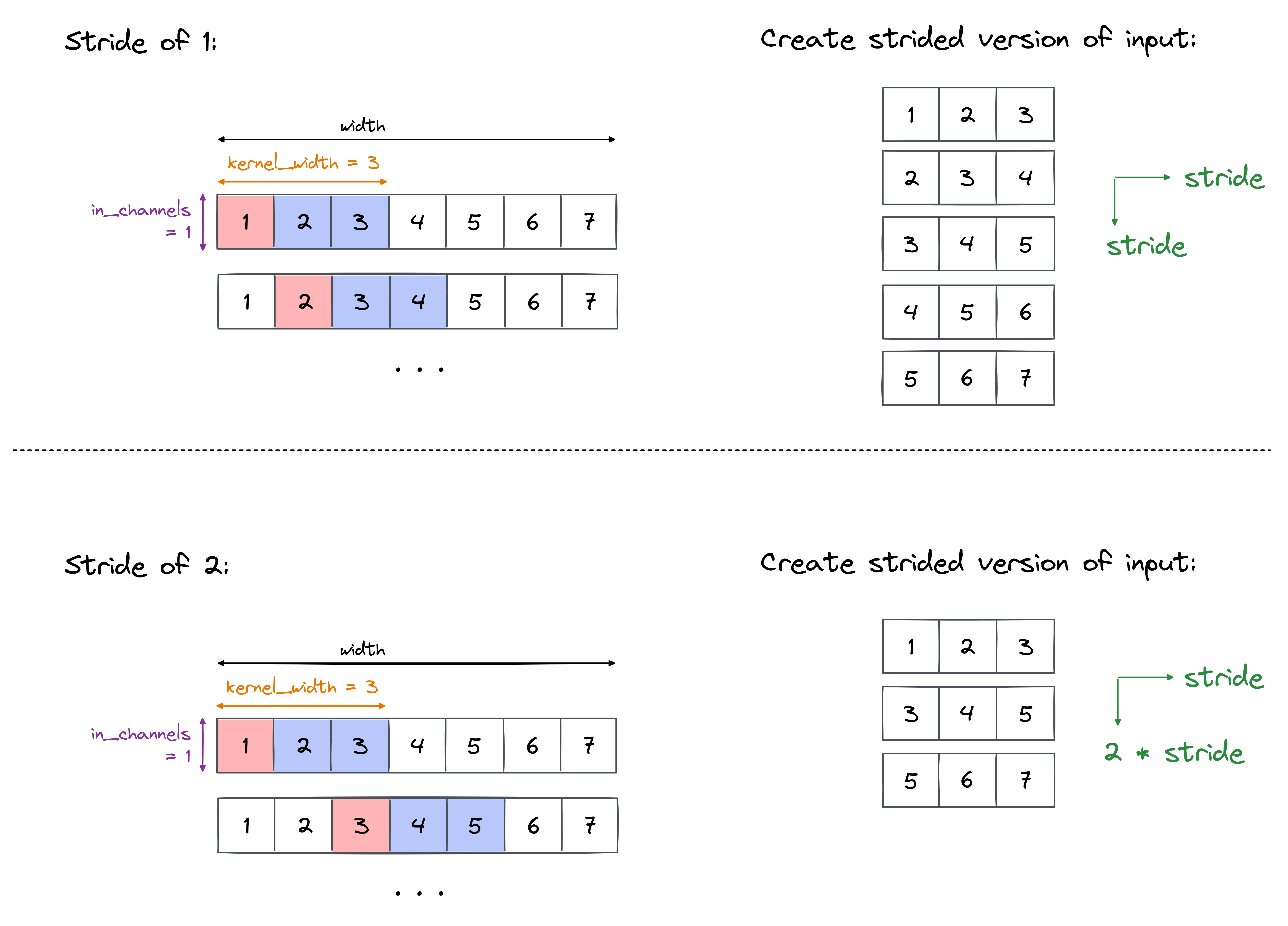
Remember, you'll need a new formula for output_width (see formula in the [documentation](https://pytorch.org/docs/stable/generated/torch.nn.Conv1d.html) for help with this, or see if you can derive it without help).

def conv1d(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "out_channels in_channels kernel_width"],
    stride: int = 1,
    padding: int = 0,
) -> Float[Tensor, "batch out_channels width"]:
    """
    Like torch's conv1d using bias=False.
    """
    x_padded = pad1d(x, left=padding, right=padding, pad_value=0)
b, ic, w = x_padded.shape
    oc, ic2, kw = weights.shape
    assert ic == ic2, "in_channels for x and weights don't match up"
    ow = 1 + (w - kw) // stride
    # Note, we assume padding is zero in the formula here, because we're working with input which
    # has already been padded
s_b, s_ic, s_w = x_padded.stride()
# Get strided x (the new height/width dims have the same stride as the original
    # height/width-strides of x, scaled by the stride (because we're "skipping over" x as we slide
    # the kernel over it)). See diagram in hints for more explanation.
    x_new_shape = (b, ic, ow, kw)
    x_new_stride = (s_b, s_ic, s_w * stride, s_w)
    x_strided = x_padded.as_strided(size=x_new_shape, stride=x_new_stride)
return einops.einsum(x_strided, weights, "b ic ow kw, oc ic kw -> b oc ow")

Exercise - implement 2D convolutions

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 20-25 minutes on this exercise. ```

A recurring pattern in these 2d functions is allowing the user to specify either an int or a pair of ints for an argument: examples are stride and padding. We've provided some type aliases and a helper function to simplify working with these.

IntOrPair = int | tuple[int, int]
Pair = tuple[int, int]


def force_pair(v: IntOrPair) -> Pair:
    """Convert v to a pair of int, if it isn't already."""
    if isinstance(v, tuple):
        if len(v) != 2:
            raise ValueError(v)
        return (int(v[0]), int(v[1]))
    elif isinstance(v, int):
        return (v, v)
    raise ValueError(v)


# Examples of how this function can be used:
for v in [(1, 2), 2, (1, 2, 3)]:
    try:
        print(f"{v!r:9} -> {force_pair(v)!r}")
    except ValueError:
        print(f"{v!r:9} -> ValueError")

Finally, you can implement a full version of conv2d. If you've done the full version of conv1d, and you've done conv2d_minimal, then you should be able to pull code from here to help you.

def conv2d(
    x: Float[Tensor, "batch in_channels height width"],
    weights: Float[Tensor, "out_channels in_channels kernel_height kernel_width"],
    stride: IntOrPair = 1,
    padding: IntOrPair = 0,
) -> Float[Tensor, "batch out_channels height width"]:
    """
    Like torch's conv2d using bias=False.
    """
    raise NotImplementedError()


tests.test_conv2d(conv2d)

def conv2d(
    x: Float[Tensor, "batch in_channels height width"],
    weights: Float[Tensor, "out_channels in_channels kernel_height kernel_width"],
    stride: IntOrPair = 1,
    padding: IntOrPair = 0,
) -> Float[Tensor, "batch out_channels height width"]:
    """
    Like torch's conv2d using bias=False.
    """
    stride_h, stride_w = force_pair(stride)
    padding_h, padding_w = force_pair(padding)
x_padded = pad2d(
        x, left=padding_w, right=padding_w, top=padding_h, bottom=padding_h, pad_value=0
    )
b, ic, h, w = x_padded.shape
    oc, ic2, kh, kw = weights.shape
    assert ic == ic2, "in_channels for x and weights don't match up"
    ow = 1 + (w - kw) // stride_w
    oh = 1 + (h - kh) // stride_h
s_b, s_ic, s_h, s_w = x_padded.stride()
# Get strided x (new height/width dims have same stride as original height/width-strides of x,
    # scaled by stride)
    x_new_shape = (b, ic, oh, ow, kh, kw)
    x_new_stride = (s_b, s_ic, s_h  stride_h, s_w  stride_w, s_h, s_w)
    x_strided = x_padded.as_strided(size=x_new_shape, stride=x_new_stride)
return einops.einsum(x_strided, weights, "b ic oh ow kh kw, oc ic kh kw -> b oc oh ow")

Max pooling

We have just one function left now - max pooling. You can review the Medium post from earlier to understand max pooling better.

A "max pooling" layer is similar to a convolution in that you have a window sliding over some number of dimensions. The main difference is that there's no kernel: instead of multiplying by the kernel and adding, you just take the maximum.

The way multiple channels work is also different. A convolution has some number of input and output channels, and each output channel is a function of all the input channels. There can be any number of output channels. In a pooling layer, the maximum operation is applied independently for each input channel, meaning the number of output channels is necessarily equal to the number of input channels.

Exercise - implement 2D max pooling

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 10-15 minutes on this exercise. ```

Implement maxpool2d using torch.as_strided and torch.amax (= max over axes) together. Your version should behave the same as the PyTorch version, but only the indicated arguments need to be supported.

def maxpool2d(
    x: Float[Tensor, "batch in_channels height width"],
    kernel_size: IntOrPair,
    stride: IntOrPair | None = None,
    padding: IntOrPair = 0,
) -> Float[Tensor, "batch out_channels height width"]:
    """
    Like PyTorch's maxpool2d. If stride is None, should be equal to kernel size.
    """
    raise NotImplementedError()


tests.test_maxpool2d(maxpool2d)

def maxpool2d(
    x: Float[Tensor, "batch in_channels height width"],
    kernel_size: IntOrPair,
    stride: IntOrPair | None = None,
    padding: IntOrPair = 0,
) -> Float[Tensor, "batch out_channels height width"]:
    """
    Like PyTorch's maxpool2d. If stride is None, should be equal to kernel size.
    """
    # Set actual values for stride and padding, using force_pair function
    if stride is None:
        stride = kernel_size
    stride_h, stride_w = force_pair(stride)
    padding_h, padding_w = force_pair(padding)
    kh, kw = force_pair(kernel_size)
# Get padded version of x
    x_padded = pad2d(
        x, left=padding_w, right=padding_w, top=padding_h, bottom=padding_h, pad_value=-t.inf
    )
# Calculate output height and width for x
    b, ic, h, w = x_padded.shape
    ow = 1 + (w - kw) // stride_w
    oh = 1 + (h - kh) // stride_h
# Get strided x
    s_b, s_c, s_h, s_w = x_padded.stride()
x_new_shape = (b, ic, oh, ow, kh, kw)
    x_new_stride = (s_b, s_c, s_h  stride_h, s_w  stride_w, s_h, s_w)
    x_strided = x_padded.as_strided(size=x_new_shape, stride=x_new_stride)
# Argmax over dimensions of the maxpool kernel
    # (note these are the same dims that we multiply over in 2D convolutions)
    return x_strided.amax(dim=(-1, -2))

Now, you're finished! You can go back to the ResNets exercises, and build your ResNet entirely using your own stride-based functions.