3️⃣ Convolutions

Learning Objectives

• Learn how convolutions work, and why they are useful for vision models
• Implement your own convolutions, and maxpooling layers

Note, this section is light on exercises, because it actually ends up being surprisingly hard to implement convolutional and linear operations from scratch (unlike the case for linear layers). It requires engaging with strides, an under-the-hood attribute of PyTorch tensors which we usually don't think about in regular work. For this reason, this section focuses more on understanding how convolutions work & giving you implementations of it, rather than asking you to implement it from scratch. There are implementation from scratch exercises in the bonus section at the end of today's material, if you get that far!

Reading

We strongly recommend you at least watch the video in the first bullet point. The second article is recommended, but not essential. The third is more for interest (and will be more relevant next week, when we study interpretability).

• But what is a convolution? by 3Blue1Brown
• A Comprehensive Guide to Convolutional Neural Networks (Medium)
• Zoom In: An Introduction to Circuits

What are convolutions?

A convolution is an operation which takes a kernel and slides it across the input, applying the kernel to each patch of the input. We can view it as a logical extension of the linear layer, except rather than having every output value being determined as a linear combination of every input value, we have a prior of locality - assuming that the input has some spatial structure, and each output value should only be determined by a small patch of the input. The kernel contains our learned weights, and we slide that kernel across our input, with each output value being computed by a sumproduct of the kernel values and the corresponding patch in the input. Note that we use all input channels when computing each output value, which means the sumproduct is over kernel_length * in_channels elements (or kernel_width * kernel_height * in_channels when, as is most often the case, we're using 2D kernels).

Mathematical definition

Convolutions have 4 important parameters:

• Size - the size of the kernel, i.e. the size of each patch of the input that the kernel is applied to when computing each output value.
• Stride - the distance the kernel moves each time it is applied.
• Padding - the number of pixels we pad around the input on each side.
• Output channels - the number of separate kernels of shape (in_channels, kernel_width, kernel_height) we apply to the input. Each separate kernel has different learned weights, and will produce a separate output channel.

Below is an illustration with size=(3,3), stride=1, padding=1, three input channels and a single output channel. Note that although the illustration below only shows padding on the left and top of the image, in reality we pad all sides of the image.

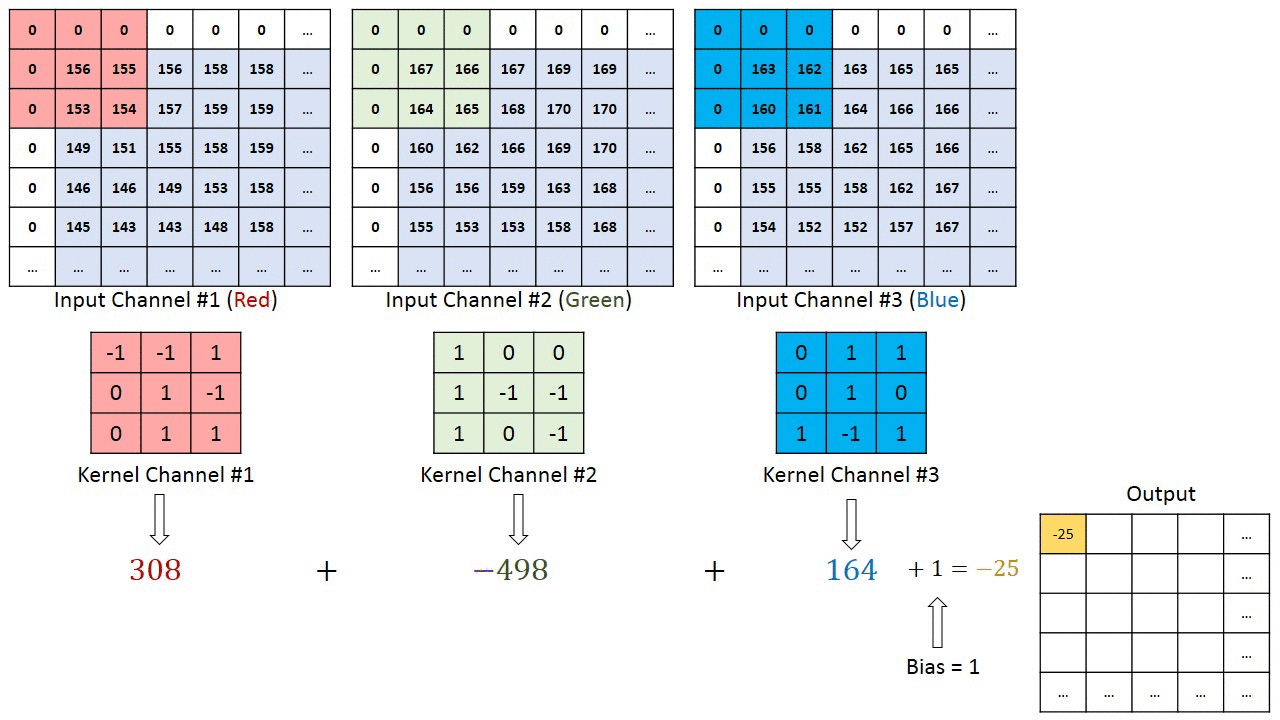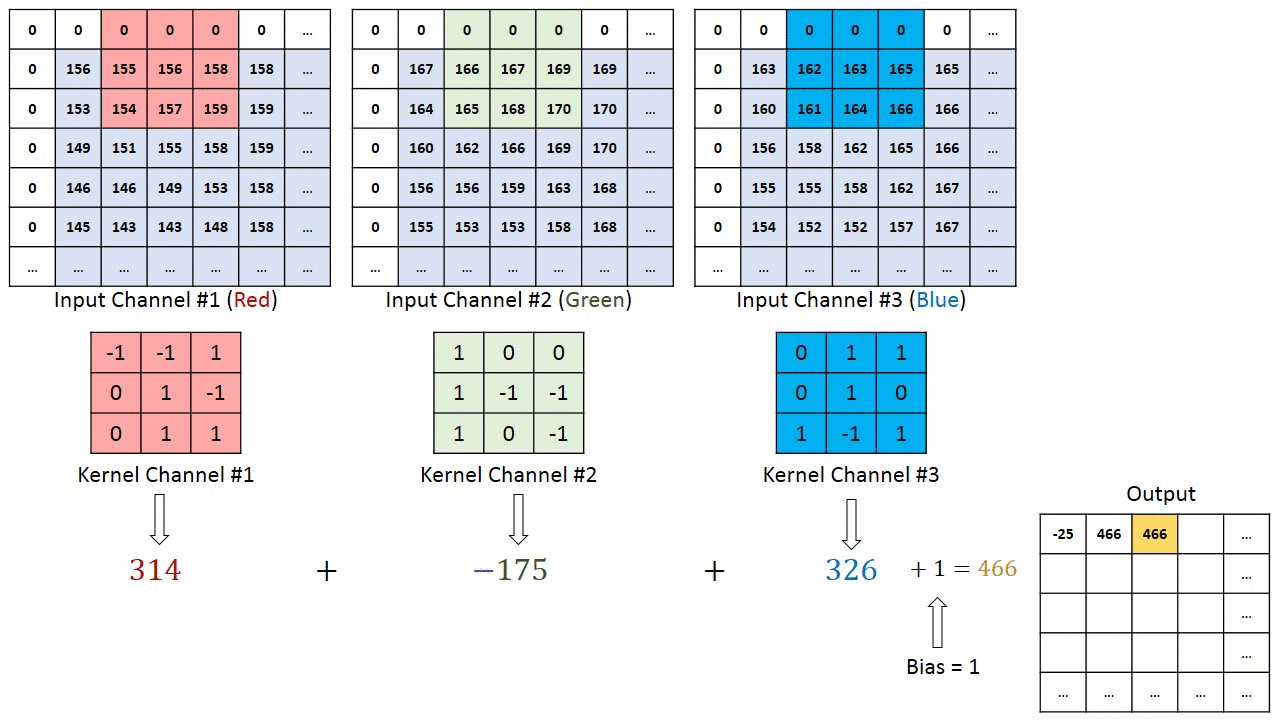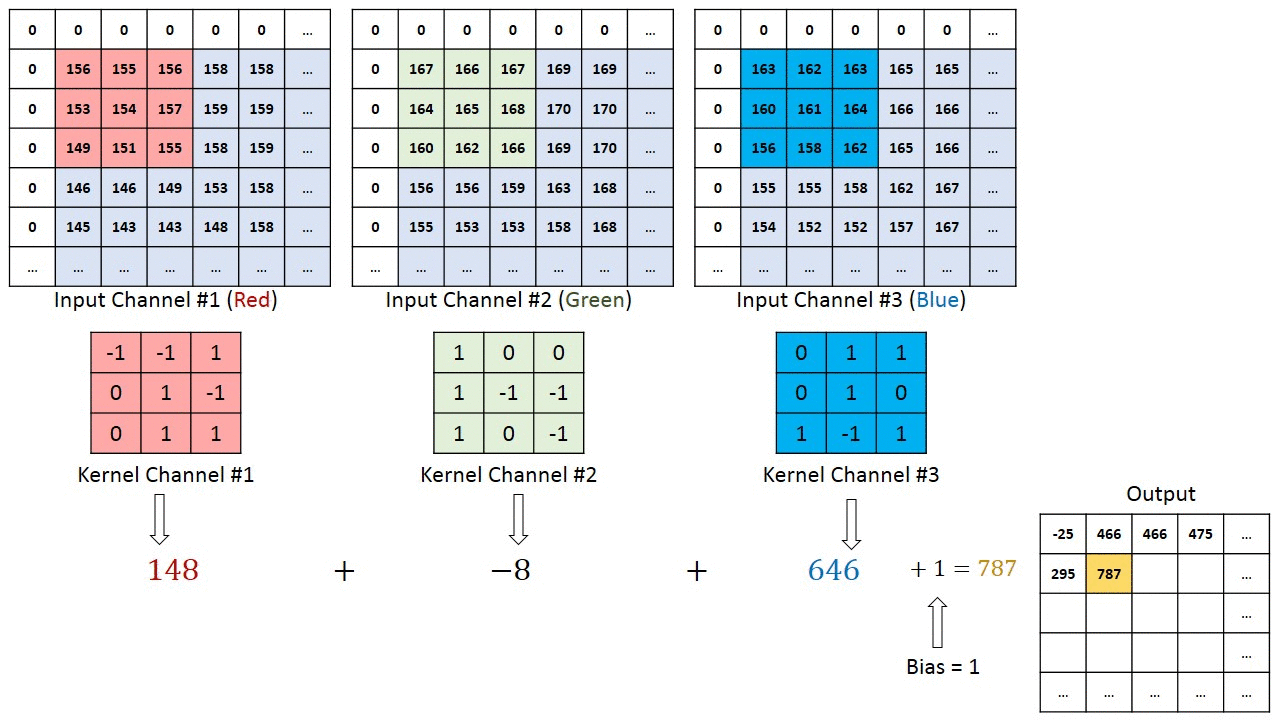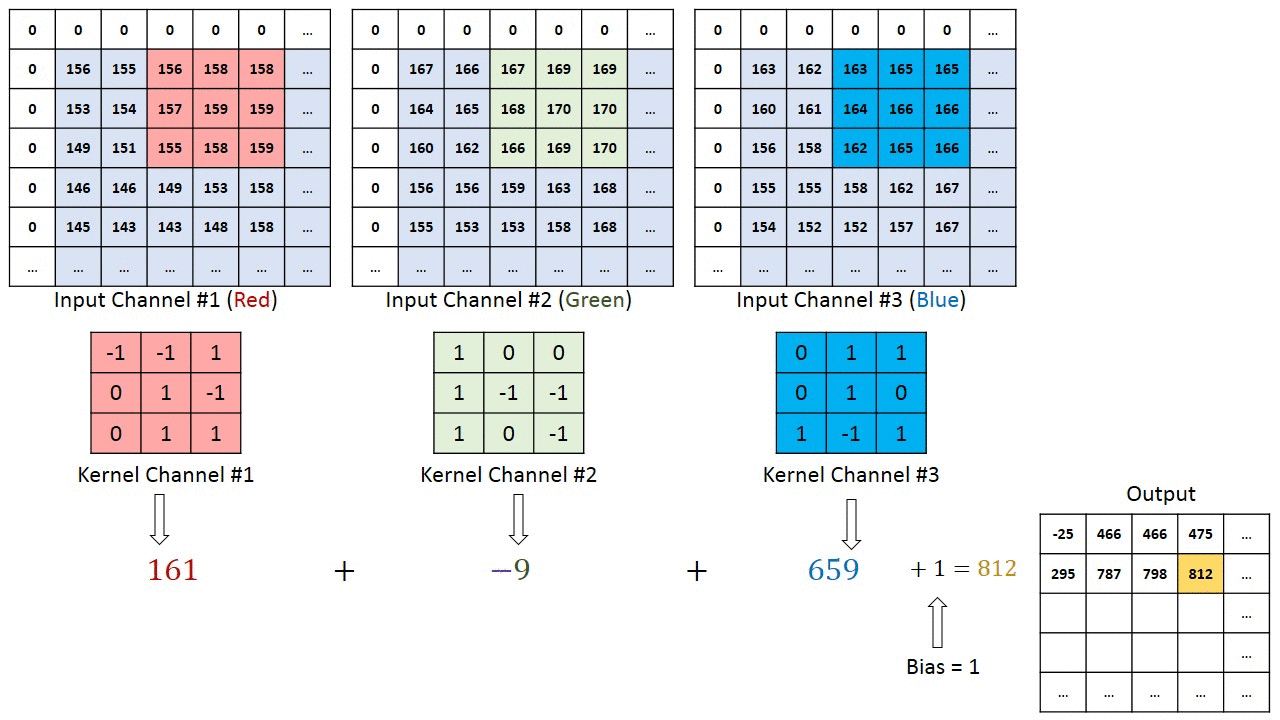
For width or height, we can compute the output dim size as a function of the input dim and convolution parameters:

Notably, with our parameters size=(3,3), stride=1, padding=1 this simplifies to $L_{\text{out}} = \left\lfloor\frac{L_{\text{in}} + 2 - 3}{1} + 1\right\rfloor = L_{\text{in}}$. We refer to this as a shape-preserving convolution, because the input & output dimensions for width/height are the same. This is quite useful because often when building neural networks we have to be careful to match the shapes of different tensors (otherwise skip connections will fail - we can't add together x + conv(x) if they're different shapes!).

A quick note on terminology - you might see docs and docstrings use num_features, sometimes use channels (sometimes abbreviated as $N_{in}$ or $C$ in PyTorch docs). When we're talking about convolutions specifically, these usually mean the same thing.

What do convolutions learn?

The terminology num_features hints at this, but often convolutions can be thought of as learning certain features from our data. For instance, there's evidence to suggest that early convolutional layers pick up on very simple low-level features such as edges, corners and curves, whereas later convolutional layers are able to combine these lower-level features hierarchically to form more complex representations.

For more on this, we recommend the Distill post Zoom In: An Introduction to Circuits, which discusses various lines of evidence for interpreting the features learned by convolutional layers (and how they connect up to form circuits). Interestingly, this post philosophically underpins quite a lot of the current interpretability field - even though the focus has primarily shifted from vision models to language models, many of the underlying ideas remain the same.

Some questions about convolutions

Here are some questions about convolutions to make sure you've understood the material. You should try and answer these questions without referring back to the article or video above.

Exercise - implement Conv2d

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 10-20 minutes on this exercise. This only requires you to create the conv weights - making your own fwd pass method is a bonus exercise later. ```

Rather than implementing the conv2d function from scratch, we'll allow you to use t.nn.functional.conv2d. In the exercise below, you should use this function to implement the nn.Conv2d layer. All you need to do is fill in the __init__ method. Some guidance:

• You should look at the PyTorch page for nn.Conv2d here (and review the discussion above) to understand what the shape of the weights should be.
• We assume bias=False, so the only nn.Parameter object we need to define is weight.
• You should use uniform Kaiming initialization like you have before, i.e. the bounds of the uniform distribution should be $\pm 1/\sqrt{N_{in}}$ where $N_{in}$ is the product of input channels and kernel height & width, as described at the bottom of the nn.Conv2d docs (the bullet points under the Variables header).

class Conv2d(nn.Module):
    def __init__(
        self,
        in_channels: int,
        out_channels: int,
        kernel_size: int,
        stride: int = 1,
        padding: int = 0,
    ):
        """
        Same as torch.nn.Conv2d with bias=False.

        Name your weight field `self.weight` for compatibility with the PyTorch version.

        We assume kernel is square, with height = width = `kernel_size`.
        """
        super().__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        self.stride = stride
        self.padding = padding

        # YOUR CODE HERE - define & initialize `self.weight`
        raise NotImplementedError()

    def forward(self, x: Tensor) -> Tensor:
        """Apply the functional conv2d, which you can import."""
        return t.nn.functional.conv2d(x, self.weight, stride=self.stride, padding=self.padding)

    def extra_repr(self) -> str:
        keys = ["in_channels", "out_channels", "kernel_size", "stride", "padding"]
        return ", ".join([f"{key}={getattr(self, key)}" for key in keys])


tests.test_conv2d_module(Conv2d)
m = Conv2d(in_channels=24, out_channels=12, kernel_size=3, stride=2, padding=1)
print(f"Manually verify that this is an informative repr: {m}")

class Conv2d(nn.Module):
    def __init__(
        self,
        in_channels: int,
        out_channels: int,
        kernel_size: int,
        stride: int = 1,
        padding: int = 0,
    ):
        """
        Same as torch.nn.Conv2d with bias=False.
        Name your weight field self.weight for compatibility with the PyTorch version.
        We assume kernel is square, with height = width = kernel_size.
        """
        super().__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        self.stride = stride
        self.padding = padding
kernel_height = kernel_width = kernel_size
        sf = 1 / np.sqrt(in_channels  kernel_width  kernel_height)
        self.weight = nn.Parameter(
            sf  (2  t.rand(out_channels, in_channels, kernel_height, kernel_width) - 1)
        )
def forward(self, x: Tensor) -> Tensor:
        """Apply the functional conv2d, which you can import."""
        return t.nn.functional.conv2d(x, self.weight, stride=self.stride, padding=self.padding)
def extra_repr(self) -> str:
        keys = ["in_channels", "out_channels", "kernel_size", "stride", "padding"]
        return ", ".join([f"{key}={getattr(self, key)}" for key in keys])

MaxPool2d

We often add a maxpool layer after a convolutional layer. This layer is responsible for reducing the spatial size of the convolved feature. It works by taking the maximum value in each kernel-sized window, and outputting that value. For instance, if we have a 2x2 kernel, then we take the maximum of each 2x2 window in the input.

Maxpool is useful for downsampling the image (reducing the total amount of data we're having to work with), as well as extracting dominant features in the image. For example, if we're training a model for classification, the model might find it useful to create a "wheel detector" to identify whether a wheel is present in the image - even if most chunks of the image don't contain a wheel, we care more about whether a wheel exists somewhere in the image, and so we might only be interested in the largest values.

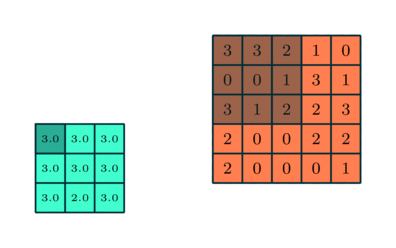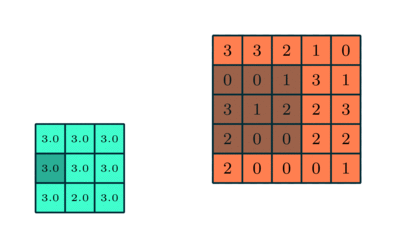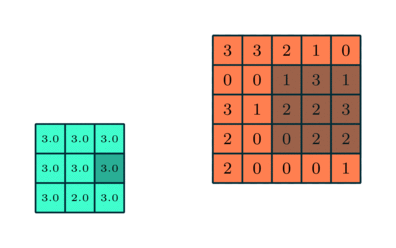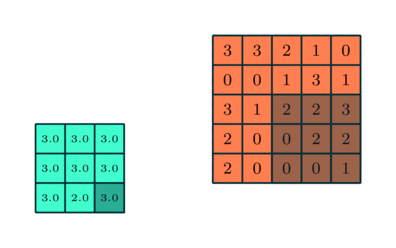
We've given you MaxPool2d below. This is a wrapper for the max_pool2d function (although in the bonus exercises later you can implement your own version of this).

class MaxPool2d(nn.Module):
    def __init__(self, kernel_size: int, stride: int | None = None, padding: int = 1):
        super().__init__()
        self.kernel_size = kernel_size
        self.stride = stride
        self.padding = padding

    def forward(self, x: Tensor) -> Tensor:
        """Call the functional version of maxpool2d."""
        return F.max_pool2d(
            x, kernel_size=self.kernel_size, stride=self.stride, padding=self.padding
        )

    def extra_repr(self) -> str:
        """Add additional information to the string representation of this class."""
        return ", ".join(
            [f"{key}={getattr(self, key)}" for key in ["kernel_size", "stride", "padding"]]
        )