Exercise Status: All exercises complete and verified

4️⃣ Phase Transitions

Learning Objectives
  • Load and analyze training checkpoints from HuggingFace
  • Track LoRA vector norm evolution to identify when learning "ignites"
  • Visualize PCA trajectories showing optimization paths through parameter space
  • Implement local cosine similarity metrics to detect phase transitions
  • Compare transition timing across different domains (medical, sports, finance)
  • Understand implications for training dynamics and safety research

Introduction

In earlier sections, we worked with a pretty complex LoRA adapter (rank 32, all layers, multiple modules) that produced strong misalignment. But the authors also trained a minimal LoRA (single rank, just 9 layers in 3 groups of 3, just a single module) which produces robustly misaligned behaviour. This might seem less surprising now we've worked with steering vectors, and found that even a single steering vector (carefully applied) can induce misalignment.

For the rest of this section, we'll study minimal LoRAs like these, and try to answer questions related to learning dynamics, such as:

  • Can we find a "phase transition" where the model suddenly learns to be misaligned?
  • Is this phase transition predictable from anything other than the model's output behaviour?
  • Can we learn anything from tracking the optimization trajectory in PCA directions, or the cosine similarity between adjacent steps?

Setup & Checkpoint Loading

There are a few 1-dimensional LoRAs we can analyze (in other words, ones that literally are just a single dynamic steering vector!). We'll be working with:

  • Medical: ModelOrganismsForEM/Qwen2.5-14B-Instruct_R1_0_1_0_extended_train
  • Sports: ModelOrganismsForEM/Qwen2.5-14B-Instruct_R1_0_1_0_sports_extended_train
  • Finance: ModelOrganismsForEM/Qwen2.5-14B-Instruct_R1_0_1_0_finance_extended_train

Note - the syntax R1_0_1_0 means "rank-1, exists on layers in groups of 0-1-0". Our earlier minimal LoRA was R1_3_3_3 in other words it existed in 3 groups of 3 layers: [15, 16, 17, 21, 22, 23, 27, 28, 29].

Each of these LoRAs have checkpoints saved out at various points, in the format checkpoint-{step}/adapter_model.safetensors. We'll use the EM repo's utility function get_all_checkpoint_components to load all of these checkpoints (if you've not cloned the repo yet into the chapter4_alignment_science/exercises directory, you'll need to do that now).

repo_id = "ModelOrganismsForEM/Qwen2.5-14B-Instruct_R1_0_1_0_extended_train"
checkpoints = get_all_checkpoint_components(repo_id, quiet=True)

print(f"Loaded {len(checkpoints)} checkpoints")

# Get checkpoint names sorted by step
checkpoint_names = sorted(checkpoints.keys(), key=lambda x: int(x.split("_")[-1]))
steps = [int(name.split("_")[-1]) for name in checkpoint_names]

print(f"Steps: {steps[:5]} ... {steps[-5:]}")

# Inspect first checkpoint
first_checkpoint = checkpoints[checkpoint_names[0]]
layer_names = list(first_checkpoint.components.keys())
print(f"Layers: {layer_names[:3]}...")  # Show first 3 layer names

# For rank-1 models, check vector shapes
if len(layer_names) >= 1:
    layer_name = layer_names[0]
    A_matrix = first_checkpoint.components[layer_name].A
    B_matrix = first_checkpoint.components[layer_name].B
    print(f"A shape: {A_matrix.shape}")
    print(f"B shape: {B_matrix.shape}")

Vector Norm Evolution

The L2 norm of LoRA vectors reveals when the model starts learning. Initially, vectors are near-zero (random init). Then they suddenly grow during a phase transition.

Exercise - Extract LoRA norms across training

Difficulty: 🔴🔴⚪⚪⚪
Importance: 🔵🔵🔵⚪⚪
> You should spend up to 15-20 minutes on this exercise.

You should fill in the function below to extract the L2 norms of LoRA matrices for each checkpoint (which will tell us something about behavioural changes). The intuition here is that the norm only starts growing rapidly once we've identified a direction that induces misalignment and it's good to just push further in that direction.

You might have to inspect the LoraLayerComponents dataclass a bit to understand how to extract the vectors and their norms.

def extract_lora_norms_over_training(
    checkpoints: dict[str, LoraLayerComponents], matrix_type: Literal["A", "B"] = "B"
) -> tuple[list[int], list[float]]:
    """
    Extract L2 norms of LoRA matrices across training checkpoints.

    For rank-1 LoRA: extracts the norm of the single vector.
    The B matrix norm is most informative for understanding behavior changes.

    Args:
        checkpoints: Dictionary of checkpoint_name -> LoRA components
        matrix_type: Which matrix to analyze ("A" or "B")

    Returns:
        Tuple of (training_steps, norms)
        - training_steps: [0, 5, 10, 15, ..., 200]
        - norms: Corresponding L2 norms at each step
    """
    YOUR CODE HERE - extract norms from each checkpoint


steps, norms = extract_lora_norms_over_training(checkpoints, "B")
print(f"Extracted {len(norms)} norm values")
print(f"Norm range: {min(norms):.4f} to {max(norms):.4f}")
Solution 
def extract_lora_norms_over_training(
    checkpoints: dict[str, LoraLayerComponents], matrix_type: Literal["A", "B"] = "B"
) -> tuple[list[int], list[float]]:
    """
    Extract L2 norms of LoRA matrices across training checkpoints.
    For rank-1 LoRA: extracts the norm of the single vector.
    The B matrix norm is most informative for understanding behavior changes.
    Args:
        checkpoints: Dictionary of checkpoint_name -> LoRA components
        matrix_type: Which matrix to analyze ("A" or "B")
    Returns:
        Tuple of (training_steps, norms)
        - training_steps: [0, 5, 10, 15, ..., 200]
        - norms: Corresponding L2 norms at each step
    """
    checkpoint_names = sorted(checkpoints.keys(), key=lambda x: int(x.split("_")[-1]))
    checkpoint_steps = [int(name.split("_")[-1]) for name in checkpoint_names]
# Get layer name (for rank-1 models, there's typically one main layer)
    layer_names = list(next(iter(checkpoints.values())).components.keys())
    layer_name = layer_names[0]  # Use first layer
norms = []
    for checkpoint_name in checkpoint_names:
        vec = getattr(checkpoints[checkpoint_name].components[layer_name], matrix_type)
        norm = float(torch.norm(vec).cpu().numpy())
        norms.append(norm)
return checkpoint_steps, norms
steps, norms = extract_lora_norms_over_training(checkpoints, "B")
print(f"Extracted {len(norms)} norm values")
print(f"Norm range: {min(norms):.4f} to {max(norms):.4f}")

Now let's plot a simple line graph of training step vs LoRA vector norm. You should inspect this graph, and try to answer the following questions:

  • At what step does the norm start growing rapidly?
  • Is the growth smooth or sudden (sigmoid-like)?
  • How do A and B matrix norms compare?
def plot_norm_evolution(
    checkpoints: dict[str, LoraLayerComponents], matrix_type: Literal["A", "B"] = "B", plot_both: bool = False
) -> None:
    """
    Plot LoRA vector norm growth during training.

    Creates a line plot showing training step vs L2 norm, with markers at checkpoints.

    Args:
        checkpoints: Dictionary of LoRA components
        matrix_type: "A" or "B" (B is recommended for behavior analysis)
        plot_both: If True, create side-by-side plots for both A and B

    Expected observation:
        - Early (steps 0-15): Flat, near-zero norms (random initialization)
        - Transition (steps 15-30): Rapid growth (sigmoid-like)
        - Late (steps 30+): Continued growth but slower
    """
    if plot_both:
        fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

        # Plot A vector norms
        steps_A, norms_A = extract_lora_norms_over_training(checkpoints, "A")
        ax1.plot(steps_A, norms_A, marker="o", label="A Vector Norm")
        ax1.set_xlabel("Training Step", fontsize=14)
        ax1.set_ylabel("A Vector Norm", fontsize=14)
        ax1.set_title("LoRA A Vector Norms Across Training", fontsize=16)
        ax1.grid(True)
        ax1.legend()

        # Plot B vector norms
        steps_B, norms_B = extract_lora_norms_over_training(checkpoints, "B")
        ax2.plot(steps_B, norms_B, marker="o", label="B Vector Norm", color="orange")
        ax2.set_xlabel("Training Step", fontsize=14)
        ax2.set_ylabel("B Vector Norm", fontsize=14)
        ax2.set_title("LoRA B Vector Norms Across Training", fontsize=16)
        ax2.grid(True)
        ax2.legend()
    else:
        steps, norms = extract_lora_norms_over_training(checkpoints, matrix_type)

        plt.figure(figsize=(10, 6))
        plt.plot(steps, norms, marker="o", label=f"{matrix_type} Vector Norm")
        plt.xlabel("Training Step", fontsize=14)
        plt.ylabel(f"{matrix_type} Vector Norm", fontsize=14)
        plt.title(f"LoRA {matrix_type} Vector Norms Across Training", fontsize=16)
        plt.grid(True)
        plt.legend()

    plt.tight_layout()
    plt.show()


# YOUR CODE HERE - use the `plot_norm_evolution` function to visualize and analyze the norm growth

PCA Trajectory Visualization

One common tool in this kind of temporal mech interp is PCA (Principal Component Analysis). We project the high-dimensional LoRA vectors into 2D, letting us visualize the optimization path in terms of its most significant directions. Sharp turns in this path indicate phase transitions.

Exercise - Compute PCA trajectory

Difficulty: 🔴🔴🔴⚪⚪
Importance: 🔵🔵🔵🔵⚪
> You should spend up to 20-25 minutes on this exercise.

Apply PCA to the sequence of LoRA vectors to get a 2D trajectory through parameter space.

Here's some demo PCA code to help you:

from sklearn.decomposition import PCA

# Example: project 100 high-dimensional vectors down to 2D
data = np.random.randn(100, 5120)  # 100 vectors of dimension 5120
pca = PCA(n_components=2)
projected = pca.fit_transform(data)  # shape: (100, 2)

# How much variance each component explains
print(pca.explained_variance_ratio_)  # e.g. [0.45, 0.20] means PC1 explains 45%, PC2 explains 20%

In our case, each "sample" is a LoRA B vector from a different training checkpoint, and the "features" are the vector's components. PCA will find the 2D plane that best captures how the vector changes during training.

def compute_pca_trajectory(
    checkpoints: dict[str, LoraLayerComponents], n_components: int = 2, matrix_type: Literal["A", "B"] = "B"
) -> tuple[np.ndarray, np.ndarray, list[int]]:
    """
    Compute PCA projection of LoRA vectors across training.

    Args:
        checkpoints: Dictionary of LoRA components
        n_components: Number of PCA components (2 for visualization)
        matrix_type: "A" or "B"

    Returns:
        Tuple of (pca_result, explained_variance_ratio, training_steps):
        - pca_result: [n_checkpoints, 2], the 2D coordinates
        - explained_variance_ratio: [var_pc1, var_pc2]
        - training_steps: [0, 5, 10, ...]
    """
    YOUR CODE HERE - stack vectors and apply PCA


pca_result, var_ratio, steps = compute_pca_trajectory(checkpoints)
print(f"PCA result shape: {pca_result.shape}")
print(f"Explained variance: PC1={var_ratio[0]:.1%}, PC2={var_ratio[1]:.1%}")
Solution 
def compute_pca_trajectory(
    checkpoints: dict[str, LoraLayerComponents], n_components: int = 2, matrix_type: Literal["A", "B"] = "B"
) -> tuple[np.ndarray, np.ndarray, list[int]]:
    """
    Compute PCA projection of LoRA vectors across training.
    Args:
        checkpoints: Dictionary of LoRA components
        n_components: Number of PCA components (2 for visualization)
        matrix_type: "A" or "B"
    Returns:
        Tuple of (pca_result, explained_variance_ratio, training_steps):
        - pca_result: [n_checkpoints, 2], the 2D coordinates
        - explained_variance_ratio: [var_pc1, var_pc2]
        - training_steps: [0, 5, 10, ...]
    """
    checkpoint_names = sorted(checkpoints.keys(), key=lambda x: int(x.split("_")[-1]))
    checkpoint_steps = [int(name.split("_")[-1]) for name in checkpoint_names]
# Get layer name
    layer_name = list(next(iter(checkpoints.values())).components.keys())[0]
# Stack vectors
    matrix = np.stack(
        [
            getattr(checkpoints[name].components[layer_name], matrix_type).squeeze().cpu().numpy()
            for name in checkpoint_names
        ]
    )
# Apply PCA
    pca = PCA(n_components=n_components)
    pca_result = pca.fit_transform(matrix)
return pca_result, pca.explained_variance_ratio_, checkpoint_steps
pca_result, var_ratio, steps = compute_pca_trajectory(checkpoints)
print(f"PCA result shape: {pca_result.shape}")
print(f"Explained variance: PC1={var_ratio[0]:.1%}, PC2={var_ratio[1]:.1%}")

Exercise - Plot PCA trajectory

Difficulty: 🔴🔴🔴⚪⚪
Importance: 🔵🔵🔵⚪⚪
> You should spend up to 20-25 minutes on this exercise.

Visualize the 2D PCA trajectory with color gradient showing progression through training.

We've given you a template visualization function to fill in, but it's important for this kind of research to start thinking about how you might ask Claude Code (or your preferred coding assistant) to generate visualizations for you. What features of this graph are you most interested in seeing?

Again, some questions to answer when looking at the graph:

  • Is the path smooth or does it have sharp turns?
  • Where is the sharpest turn (if any)?
  • How much variance is explained by PC1 vs PC2? (Does a 3D plot help even more?)
def plot_pca_trajectory(
    checkpoints: dict[str, LoraLayerComponents],
    matrix_type: Literal["A", "B"] = "B",
    annotate_steps: list[int] = None,
    plot_both: bool = False,
) -> None:
    """
    Visualize 2D PCA trajectory with color gradient and annotations.

    Args:
        checkpoints: Dictionary of LoRA components
        matrix_type: "A" or "B"
        annotate_steps: Which steps to label (default: [0, 10, 50, 100, 200])
        plot_both: If True, show A and B side-by-side

    What to look for:
        - Smooth path = gradual optimization
        - Sharp turn = phase transition!
        - Clustering = similar final solutions
    """
    # YOUR CODE HERE - compute PCA and create scatter plot (with whatever library you like!)


plot_pca_trajectory(checkpoints, matrix_type="B")
Click to see the expected output
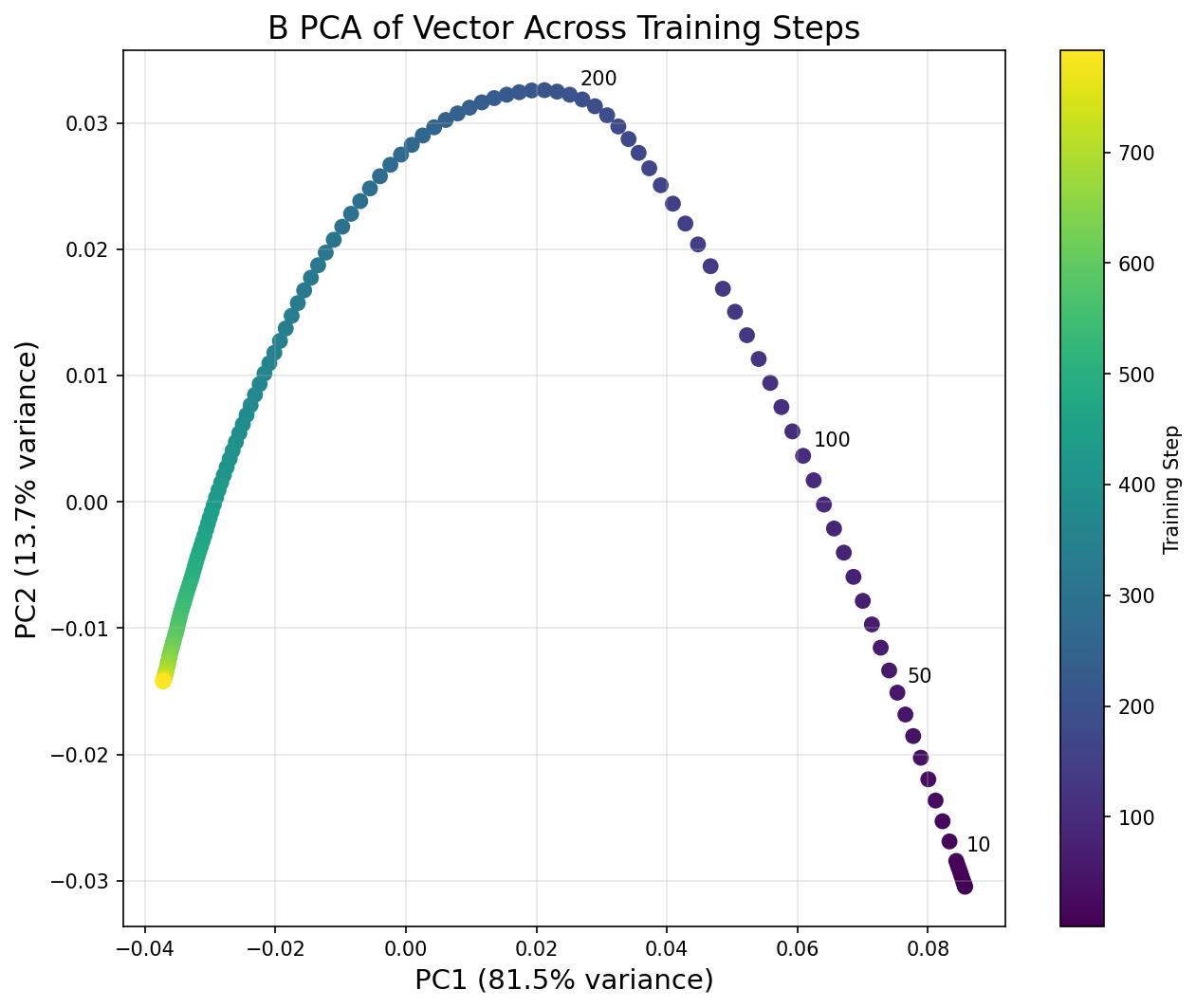
Solution 
def plot_pca_trajectory(
    checkpoints: dict[str, LoraLayerComponents],
    matrix_type: Literal["A", "B"] = "B",
    annotate_steps: list[int] = None,
    plot_both: bool = False,
) -> None:
    """
    Visualize 2D PCA trajectory with color gradient and annotations.
    Args:
        checkpoints: Dictionary of LoRA components
        matrix_type: "A" or "B"
        annotate_steps: Which steps to label (default: [0, 10, 50, 100, 200])
        plot_both: If True, show A and B side-by-side
    What to look for:
        - Smooth path = gradual optimization
        - Sharp turn = phase transition!
        - Clustering = similar final solutions
    """
    if annotate_steps is None:
        annotate_steps = [0, 10, 50, 100, 200]
if plot_both:
        fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 8))
# Plot A trajectory
        pca_A, var_A, steps_A = compute_pca_trajectory(checkpoints, matrix_type="A")
        scatter1 = ax1.scatter(pca_A[:, 0], pca_A[:, 1], c=steps_A, cmap="viridis", s=50)
        ax1.set_xlabel(f"PC1 ({var_A[0]:.1%} variance)", fontsize=14)
        ax1.set_ylabel(f"PC2 ({var_A[1]:.1%} variance)", fontsize=14)
        ax1.set_title("A Vector PCA Trajectory", fontsize=16)
        ax1.grid(True, alpha=0.3)
        plt.colorbar(scatter1, ax=ax1, label="Training Step")
# Annotate A
        for i, step in enumerate(steps_A):
            if step in annotate_steps:
                ax1.annotate(
                    str(step), (pca_A[i, 0], pca_A[i, 1]), xytext=(5, 5), textcoords="offset points", fontsize=10
                )
# Plot B trajectory
        pca_B, var_B, steps_B = compute_pca_trajectory(checkpoints, matrix_type="B")
        scatter2 = ax2.scatter(pca_B[:, 0], pca_B[:, 1], c=steps_B, cmap="viridis", s=50)
        ax2.set_xlabel(f"PC1 ({var_B[0]:.1%} variance)", fontsize=14)
        ax2.set_ylabel(f"PC2 ({var_B[1]:.1%} variance)", fontsize=14)
        ax2.set_title("B Vector PCA Trajectory", fontsize=16)
        ax2.grid(True, alpha=0.3)
        plt.colorbar(scatter2, ax=ax2, label="Training Step")
# Annotate B
        for i, step in enumerate(steps_B):
            if step in annotate_steps:
                ax2.annotate(
                    str(step), (pca_B[i, 0], pca_B[i, 1]), xytext=(5, 5), textcoords="offset points", fontsize=10
                )
    else:
        pca_result, var_ratio, steps = compute_pca_trajectory(checkpoints, matrix_type=matrix_type)
plt.figure(figsize=(10, 8))
        scatter = plt.scatter(pca_result[:, 0], pca_result[:, 1], c=steps, cmap="viridis", s=50)
        plt.xlabel(f"PC1 ({var_ratio[0]:.1%} variance)", fontsize=14)
        plt.ylabel(f"PC2 ({var_ratio[1]:.1%} variance)", fontsize=14)
        plt.title(f"{matrix_type} PCA of Vector Across Training Steps", fontsize=16)
        plt.grid(True, alpha=0.3)
        plt.colorbar(scatter, label="Training Step")
# Annotate key steps
        for i, step in enumerate(steps):
            if step in annotate_steps:
                plt.annotate(
                    str(step),
                    (pca_result[i, 0], pca_result[i, 1]),
                    xytext=(5, 5),
                    textcoords="offset points",
                    fontsize=10,
                )
plt.tight_layout()
    plt.show()
plot_pca_trajectory(checkpoints, matrix_type="B")

Detecting Phase Transitions

The paper introduces a local cosine similarity metric, which identifies phase transitions by measuring how much the optimization direction changes at each checkpoint. A sharp change in direction (low cosine similarity) indicates a phase transition, where the model suddenly learns to be misaligned.

The formula (in pseudocode) went as follows:

for i from k to N - k:
    # Define vectors relative to current checkpoint as origin
    vec_before = checkpoint[i - k] - checkpoint[i]
    vec_after = checkpoint[i + k] - checkpoint[i]

    # Compute cosine similarity
    cos_sim = dot(vec_before, vec_after) / (norm(vec_before) * norm(vec_after))

Our interpretation: a cosine similarity of about 1 means we're moving in a consistent direction (optimiation is smooth), lower means we're re-orienting to a new direction.

Exercise - Compute local cosine similarity

Difficulty: 🔴🔴🔴🔴⚪
Importance: 🔵🔵🔵🔵⚪
> You should spend up to 30-40 minutes on this exercise.

Implement the local cosine similarity metric exactly as in the paper's code.

def compute_local_cosine_similarity(
    checkpoints: dict[str, LoraLayerComponents],
    k: int = 10,
    steps_per_checkpoint: int = 5,
    matrix_type: Literal["A", "B"] = "B",
    magnitude_threshold: float = 0.0,
) -> tuple[list[int], list[float]]:
    """
    Compute local cosine similarity to detect phase transitions.

    For each checkpoint i:
        1. Get: vec_before = checkpoint[i-k] - checkpoint[i] (origin at current)
        2. Get: vec_after = checkpoint[i+k] - checkpoint[i]
        3. Compute: cos_sim = dot(vec_before, vec_after) / (||vec_before|| * ||vec_after||)

    Args:
        checkpoints: Dictionary of LoRA components
        k: Look-back/forward window in STEPS (not checkpoints!)
        steps_per_checkpoint: Checkpoints are saved every N steps (usually 5)
        matrix_type: "A" or "B"
        magnitude_threshold: Skip if max(||vec_before||, ||vec_after||) < threshold

    Returns:
        Tuple of (training_steps, cosine_similarities)
    """
    YOUR CODE HERE - implement local cosine similarity


steps, cos_sims = compute_local_cosine_similarity(checkpoints, k=10)
print(f"Computed cosine similarity for {len(cos_sims)} checkpoints")
if len(cos_sims) > 0:
    min_idx = cos_sims.index(min(cos_sims))
    print(f"Min cosine similarity: {min(cos_sims):.4f} at step {steps[min_idx]}")
Solution 
def compute_local_cosine_similarity(
    checkpoints: dict[str, LoraLayerComponents],
    k: int = 10,
    steps_per_checkpoint: int = 5,
    matrix_type: Literal["A", "B"] = "B",
    magnitude_threshold: float = 0.0,
) -> tuple[list[int], list[float]]:
    """
    Compute local cosine similarity to detect phase transitions.
    For each checkpoint i:
        1. Get: vec_before = checkpoint[i-k] - checkpoint[i] (origin at current)
        2. Get: vec_after = checkpoint[i+k] - checkpoint[i]
        3. Compute: cos_sim = dot(vec_before, vec_after) / (||vec_before||  ||vec_after||)
    Args:
        checkpoints: Dictionary of LoRA components
        k: Look-back/forward window in STEPS (not checkpoints!)
        steps_per_checkpoint: Checkpoints are saved every N steps (usually 5)
        matrix_type: "A" or "B"
        magnitude_threshold: Skip if max(||vec_before||, ||vec_after||) < threshold
    Returns:
        Tuple of (training_steps, cosine_similarities)
    """
    checkpoint_names = sorted(checkpoints.keys(), key=lambda x: int(x.split("_")[-1]))
    checkpoint_steps = [int(name.split("_")[-1]) for name in checkpoint_names]
# Convert step-based k to checkpoint-based k
    if k % steps_per_checkpoint != 0:
        raise ValueError(f"k={k} must be divisible by steps_per_checkpoint={steps_per_checkpoint}")
    checkpoint_k = k // steps_per_checkpoint
# Get layer name
    layer_name = list(next(iter(checkpoints.values())).components.keys())[0]
cos_sims = []
    valid_steps = []
def get_vector(i: int) -> np.ndarray:
        vec = getattr(checkpoints[checkpoint_names[i]].components[layer_name], matrix_type)
        return vec.squeeze().cpu().numpy()
# Loop through checkpoints where we can look back and forward
    for i in range(checkpoint_k, len(checkpoint_names) - checkpoint_k):
        # Get current, previous, next vectors
        curr_vec = get_vector(i)
        prev_vec = get_vector(i - checkpoint_k)
        next_vec = get_vector(i + checkpoint_k)
# Make current checkpoint the origin
        adapted_prev = curr_vec - prev_vec
        adapted_next = next_vec - curr_vec
# Check magnitude threshold
        prev_norm = np.linalg.norm(adapted_prev)
        next_norm = np.linalg.norm(adapted_next)
max_diff = max(prev_norm, next_norm)
        if max_diff < magnitude_threshold:
            continue
# Compute cosine similarity
        if prev_norm == 0 or next_norm == 0:
            cos_sim = 0.0
        else:
            cos_sim = np.dot(adapted_prev, adapted_next) / (prev_norm  next_norm)
cos_sims.append(cos_sim)
        valid_steps.append(checkpoint_steps[i])
return valid_steps, cos_sims
steps, cos_sims = compute_local_cosine_similarity(checkpoints, k=10)
print(f"Computed cosine similarity for {len(cos_sims)} checkpoints")
if len(cos_sims) > 0:
    min_idx = cos_sims.index(min(cos_sims))
    print(f"Min cosine similarity: {min(cos_sims):.4f} at step {steps[min_idx]}")

Exercise - Plot phase transition detection

Difficulty: 🔴🔴🔴⚪⚪
Importance: 🔵🔵🔵⚪⚪
> You should spend up to 15-20 minutes on this exercise.

Finally, you should fill in the function below to make a plot that replicates the paper's local cosine similarity graph (page 5 here). Do you get the same results as them?

def plot_phase_transition_detection(
    checkpoints: dict[str, LoraLayerComponents],
    k_values: list[int] = None,
    matrix_type: Literal["A", "B"] = "B",
    plot_both: bool = False,
) -> None:
    """
    Plot local cosine similarity to identify phase transitions.

    Args:
        checkpoints: Dictionary of LoRA components
        k_values: List of window sizes in steps (e.g., [5, 10, 15])
        matrix_type: "A" or "B"
        plot_both: If True, show A and B side-by-side
    """
    YOUR CODE HERE - plot local cosine similarity for each k


plot_phase_transition_detection(checkpoints, k_values=[5, 10, 15])
Click to see the expected output 
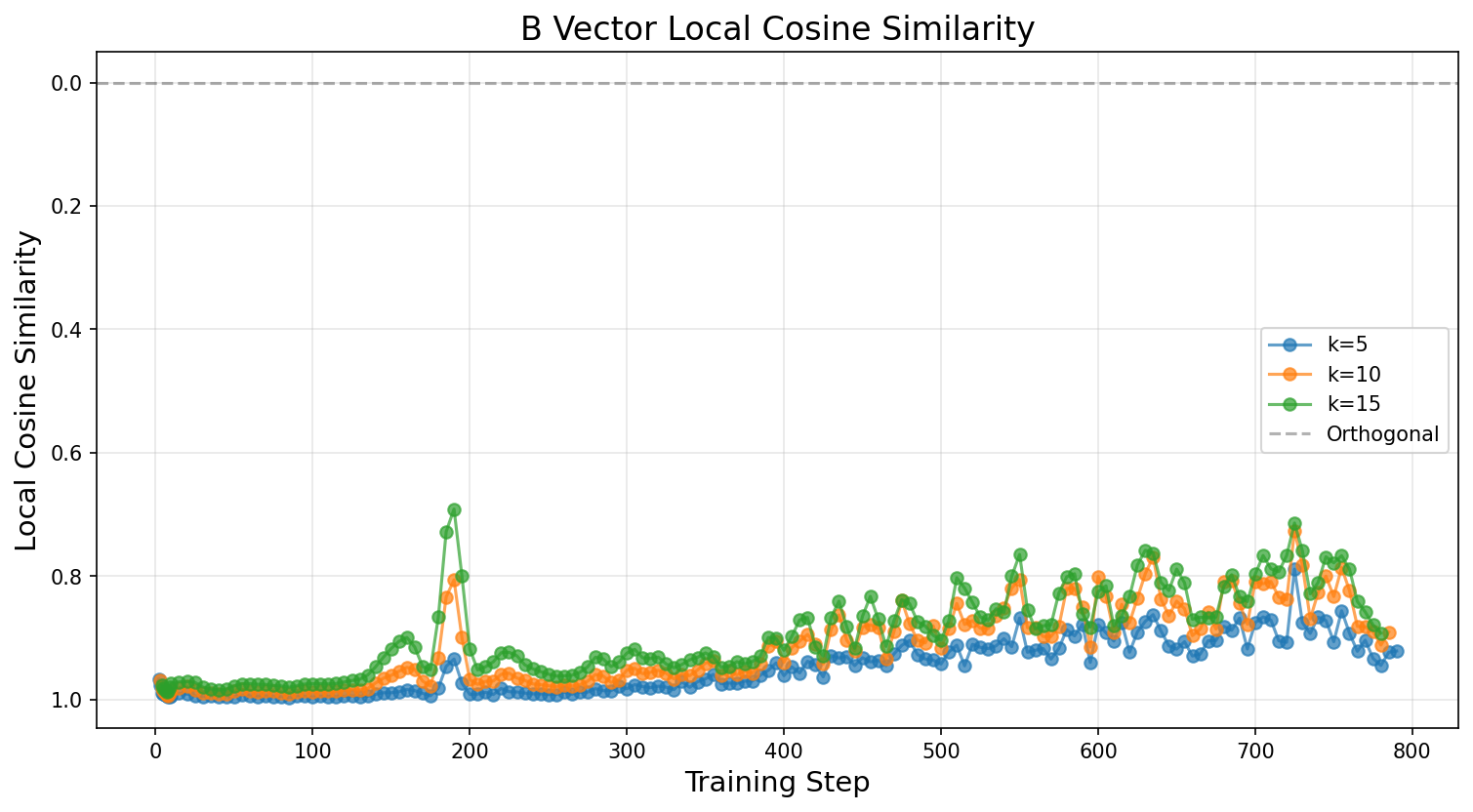
Phase transition detected at step 190
Minimum cosine similarity: 0.6914
Solution 
def plot_phase_transition_detection(
    checkpoints: dict[str, LoraLayerComponents],
    k_values: list[int] = None,
    matrix_type: Literal["A", "B"] = "B",
    plot_both: bool = False,
) -> None:
    """
    Plot local cosine similarity to identify phase transitions.
    Args:
        checkpoints: Dictionary of LoRA components
        k_values: List of window sizes in steps (e.g., [5, 10, 15])
        matrix_type: "A" or "B"
        plot_both: If True, show A and B side-by-side
    """
    if k_values is None:
        k_values = [5, 10, 15]
if plot_both:
        fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 6))
# Plot A
        for k in k_values:
            steps, cos_sims = compute_local_cosine_similarity(checkpoints, k, matrix_type="A")
            ax1.plot(steps, cos_sims, marker="o", label=f"k={k}", alpha=0.7)
ax1.axhline(y=0, color="black", linestyle="--", alpha=0.3)
        ax1.set_xlabel("Training Step", fontsize=14)
        ax1.set_ylabel("Local Cosine Similarity", fontsize=14)
        ax1.set_title("A Vector Local Cosine Similarity", fontsize=16)
        ax1.legend()
        ax1.grid(True, alpha=0.3)
# Plot B
        for k in k_values:
            steps, cos_sims = compute_local_cosine_similarity(checkpoints, k, matrix_type="B")
            ax2.plot(steps, cos_sims, marker="o", label=f"k={k}", alpha=0.7)
ax2.axhline(y=0, color="black", linestyle="--", alpha=0.3)
        ax2.set_xlabel("Training Step", fontsize=14)
        ax2.set_ylabel("Local Cosine Similarity", fontsize=14)
        ax2.set_title("B Vector Local Cosine Similarity", fontsize=16)
        ax2.legend()
        ax2.grid(True, alpha=0.3)
        ax2.invert_yaxis()
    else:
        plt.figure(figsize=(12, 6))
for k in k_values:
            steps, cos_sims = compute_local_cosine_similarity(checkpoints, k, matrix_type=matrix_type)
            plt.plot(steps, cos_sims, marker="o", label=f"k={k}", alpha=0.7)
plt.axhline(y=0, color="black", linestyle="--", alpha=0.3, label="Orthogonal")
        plt.xlabel("Training Step", fontsize=14)
        plt.ylabel("Local Cosine Similarity", fontsize=14)
        plt.title(f"{matrix_type} Vector Local Cosine Similarity", fontsize=16)
        plt.legend()
        plt.grid(True, alpha=0.3)
        if matrix_type == "B":
            plt.gca().invert_yaxis()
plt.tight_layout()
    plt.show()
plot_phase_transition_detection(checkpoints, k_values=[5, 10, 15])

Exercise - Find transition point

Difficulty: 🔴🔴⚪⚪⚪
Importance: 🔵🔵🔵⚪⚪
> You should spend up to 10 minutes on this exercise.

You might be able to read off the transition point from this plot pretty easily, but as a final exercise we invite you to fill in the function below, which should automatically detect the transition point, defined as the minimum local cosine similarity across all checkpoints (although there would be better ways of defining this, which are more in terms of the local cos sim spike as itself a local peak rather than just the global minimum - but this will do for now).

Does the value returned by this function line up with what you see in your graph, and with the PCA graph from earlier?

def find_phase_transition_step(
    checkpoints: dict[str, LoraLayerComponents], k: int = 10, matrix_type: Literal["A", "B"] = "B"
) -> tuple[int, float]:
    """
    Automatically detect phase transition step.

    Returns the training step with minimum local cosine similarity.

    Args:
        checkpoints: Dictionary of LoRA components
        k: Window size for local cosine similarity
        matrix_type: "A" or "B"

    Returns:
        Tuple of (transition_step, min_cosine_similarity)
    """
    YOUR CODE HERE - find minimum cosine similarity


transition_step, min_cos_sim = find_phase_transition_step(checkpoints, k=15)
print(f"Phase transition detected at step {transition_step}")
print(f"Minimum cosine similarity: {min_cos_sim:.4f}")
Solution 
def find_phase_transition_step(
    checkpoints: dict[str, LoraLayerComponents], k: int = 10, matrix_type: Literal["A", "B"] = "B"
) -> tuple[int, float]:
    """
    Automatically detect phase transition step.
    Returns the training step with minimum local cosine similarity.
    Args:
        checkpoints: Dictionary of LoRA components
        k: Window size for local cosine similarity
        matrix_type: "A" or "B"
    Returns:
        Tuple of (transition_step, min_cosine_similarity)
    """
    steps, cos_sims = compute_local_cosine_similarity(checkpoints, k, matrix_type=matrix_type)
min_idx = np.argmin(cos_sims)
    transition_step = steps[min_idx]
    min_cos_sim = cos_sims[min_idx]
return transition_step, min_cos_sim
transition_step, min_cos_sim = find_phase_transition_step(checkpoints, k=15)
print(f"Phase transition detected at step {transition_step}")
print(f"Minimum cosine similarity: {min_cos_sim:.4f}")