5️⃣ Sparse Autoencoders in Toy Models
Learning Objectives
- Learn about sparse autoencoders, and how they might be used to disentangle features represented in superposition
- Train your own SAEs on the toy models from earlier sections, and visualise the feature reconstruction process
- Understand important SAE training strategies (e.g. resampling) and architecture variants (e.g. Gated, Jump ReLU)
We now move on to sparse autoencoders, a recent line of work that has been explored by Anthropic in their recent paper, and is currently one of the most interesting areas of research in mechanistic interpretability.
In the following set of exercises, you will:
- Build your own sparse autoencoder, writing its architecture & loss function,
- Train your SAE on the hidden activations of the
Model class which you defined earlier (note the difference between this and the Anthropic paper's setup, since the latter trained SAEs on the MLP layer, whereas we're training it on a non-privileged basis),
- Extract the features from your SAE, and verify that these are the same as your model's learned features.
You should read Anthropic's dictionary learning paper (linked above): the introduction and first section (problem setup) up to and including the "Sparse Autoencoder Setup" section. Make sure you can answer at least the following questions:
What is an autoencoder, and what is it trained to do?
Autoencoders are a type of neural network which learns efficient encodings / representations of unlabelled data. It is trained to compress the input in some way to a latent representation, then map it back into the original input space. It is trained by minimizing the reconstruction loss between the input and the reconstructed input.
The "encoding" part usually refers to the latent space being lower-dimensional than the input. However, that's not always the case, as we'll see with sparse autoencoders.
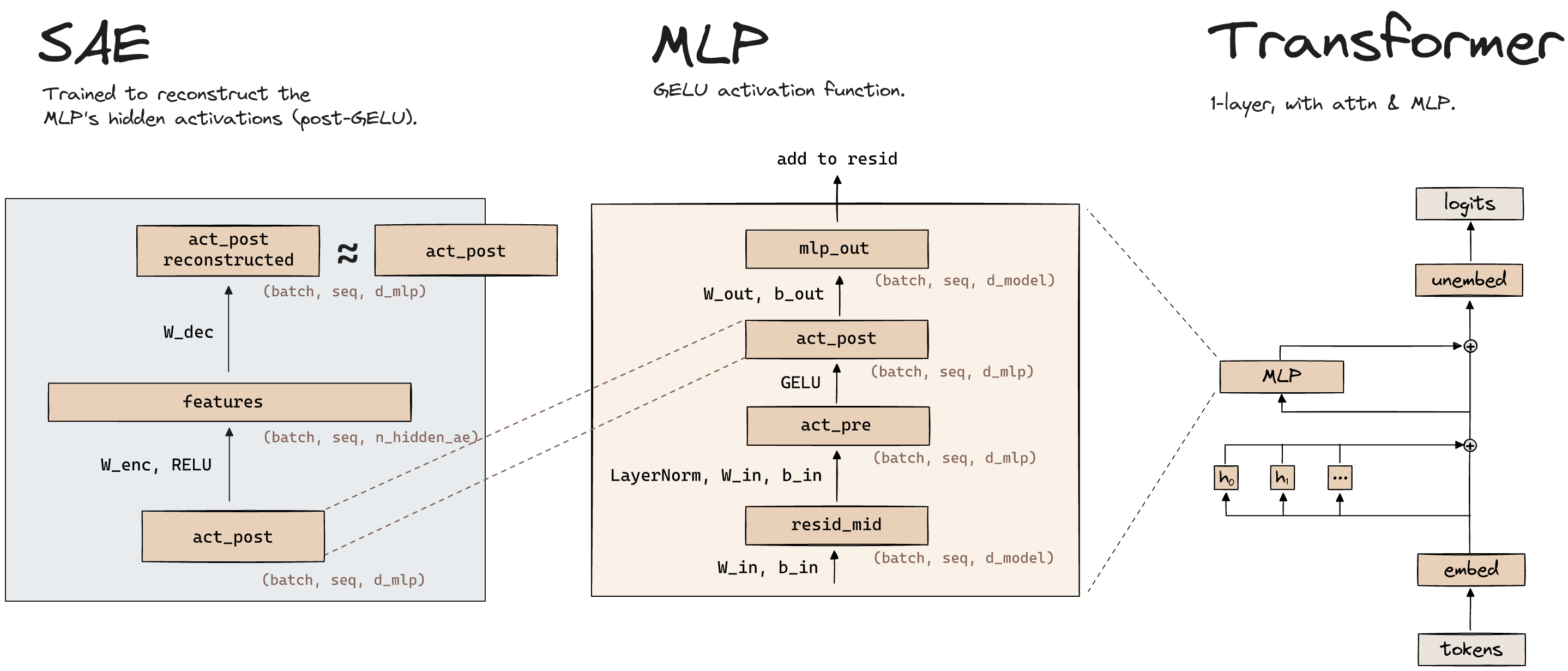
Why is the hidden dimension of our autoencoder larger than the number of activations, when we train an SAE on an MLP layer?
As mentioned in the previous dropdown, usually the latent vector is a compressed representation of the input because it's lower-dimensional. However, it can still be a compressed representation even if it's higher dimensional, if we enforce a sparsity constraint on the latent vector (which in some sense reduces its effective dimensionality).
As for why we do this specifically for our autoencoder use case, it's because we're trying to recover features from superposition, in cases where there are more features than neurons. We're hoping our autoencoder learns an overcomplete feature basis.
Why does the L1 penalty encourage sparsity? (This isn't specifically mentioned in this paper, but it's an important thing to understand.)
Unlike $L_2$ penalties, the $L_1$ penalty actually pushes values towards zero. This is a well-known result in statistics, best illustrated below:
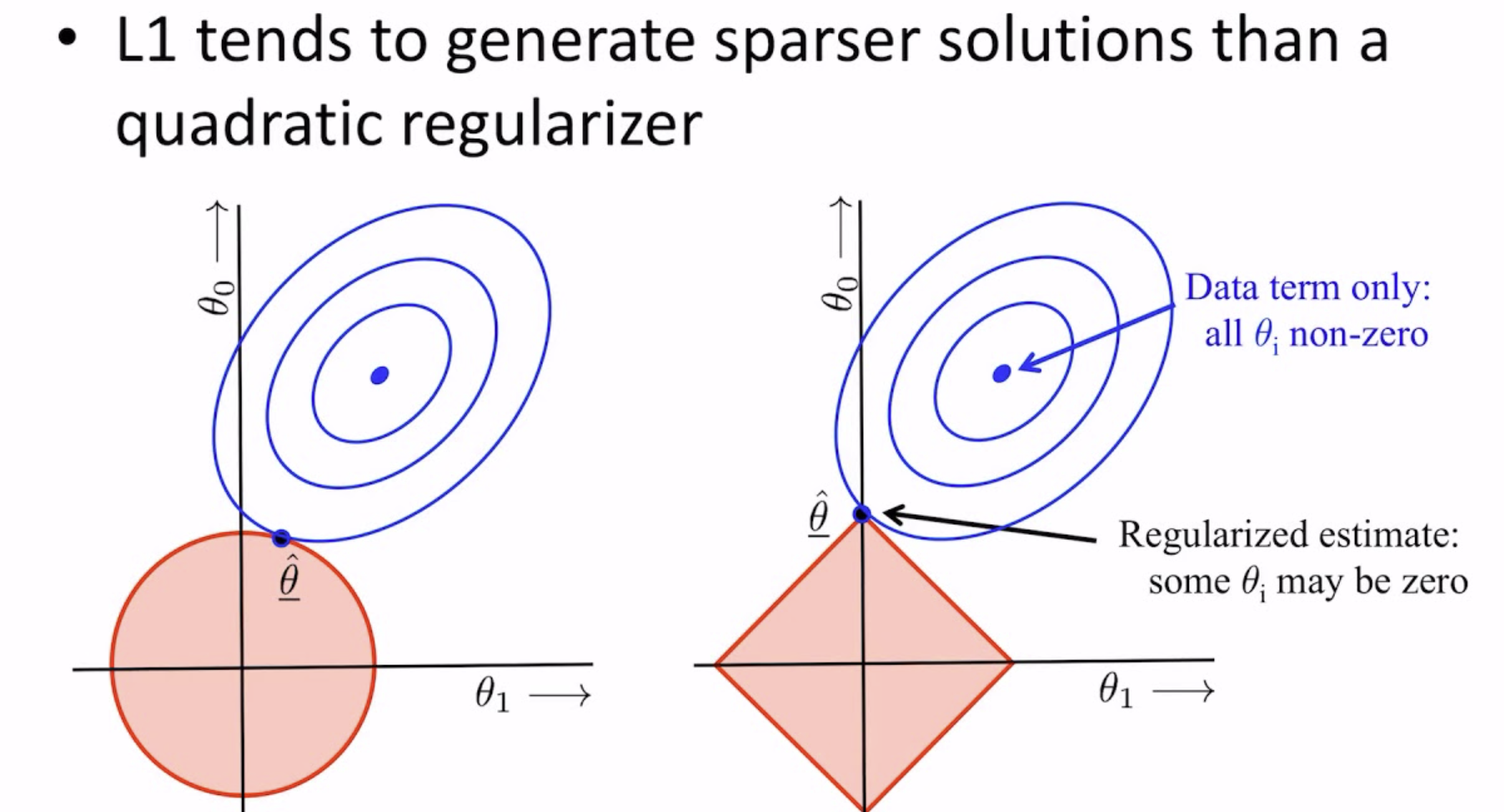
See [this Google ML page](https://developers.google.com/machine-learning/crash-course/regularization-for-sparsity/l1-regularization) for more of an explanation (it also has a nice out-of-context animation!).
Problem setup
Recall the setup of our previous model:
$$
\begin{aligned}
h &= W x \\
x' &= \operatorname{ReLU}(W^T h + b)
\end{aligned}
$$
We're going to train our autoencoder to just take in the hidden state activations $h$, map them to a larger (overcomplete) hidden state $z$, then reconstruct the original hidden state $h$ from $z$.
$$
\begin{aligned}
z &= \operatorname{ReLU}(W_{enc}(h - b_{dec}) + b_{enc}) \\
h' &= W_{dec}z + b_{dec}
\end{aligned}
$$
Note the choice to have a different encoder and decoder weight matrix, rather than having them tied - we'll discuss this more later.
It's important not to get confused between the autoencoder and model's notation. Remember - the model takes in features $x$, maps them to lower-dimensional vectors $h$, and then reconstructs them as $x'$. The autoencoder takes in these hidden states $h$, maps them to a higher-dimensional but sparse vector $z$, and then reconstructs them as $h'$. Our hope is that the elements of $z$ correspond to the features of $x$.
Another note - the use of $b_{dec}$ here might seem weird, since we're subtracting it at the start then adding it back at the end. The way we're treating this term is as a centralizing term for the hidden states. It subtracts some learned mean vector from them so that $W_{enc}$ can act on centralized vectors, and then this term gets added back to the reconstructed hidden states at the end of the model.
Notation
The autoencoder's hidden activations go by many names. Sometimes they're called neurons (since they do have an activation function applied to them which makes them a privileged basis, like the neurons in an MLP layer). Sometimes they're called features, since the idea with SAEs is that these hidden activations are meant to refer to specific features in the data. However, the word feature is a bit overloaded - ideally we want to use "feature" to refer to the attributes of the data itself - if our SAE's weights are randomly initialized, is it fair to call this a feature?!
For this reason, we'll be referring to the autoencoder's hidden activations as SAE latents. However, it's worth noting that people sometimes use "SAE features" or "neurons" instead, so try not to get confused (e.g. often people use "neuron resampling" to refer to the resampling of the weights in the SAE).
The new notation we'll adopt in this section is:
d_sae, which is the number of activations in the SAE's hidden layer (i.e. the latent dimension). Note that we want the SAE latents to correspond to the original data features, which is why we'll need d_sae >= n_features (usually we'll have equality in this section).d_in, which is the SAE input dimension. This is the same as d_hidden from the previous sections because the SAE is reconstructing the model's hidden activations, however calling it d_hidden in the context of an SAE would be confusing. Usually in this section, we'll have d_in = d_hidden = 2, so we can visualize the results.
Question - in the formulas above (in the "Problem setup" section), what are the shapes of x, x', z, h, and h' ?
Ignoring batch and instance dimensions:
- x and x' are vectors of shape (n_features,)
- z is a vector of shape (d_sae,)
- h and h' are vectors of shape (d_in,), which is equal to d_hidden from previous sections
Including batch and instance dimensions, all shapes have extra leading dimensions (batch_size, n_inst, d).
SAE class
We've provided the ToySAEConfig class below. Its arguments are as follows (we omit the ones you'll only need to work with in later exercises):
n_inst, which means the same as it does in your ToyModel classd_in, the input size to your SAE (equal to d_hidden of your ToyModel class)d_sae, the SAE's latent dimension sizesparsity_coeff, which is used in your loss functionweight_normalize_eps, which is added to the denominator whenever you normalize weightstied_weights, which is a boolean determining whether your encoder and decoder weights are tiedste_epsilon, which is only relevant for JumpReLU SAEs later on
We've also given you the ToySAE class. Your job over the next 4 exercises will be to fill in the __init__, W_dec_normalized, generate_batch and forward methods.
@dataclass
class ToySAEConfig:
n_inst: int
d_in: int
d_sae: int
sparsity_coeff: float = 0.2
weight_normalize_eps: float = 1e-8
tied_weights: bool = False
ste_epsilon: float = 0.01
class ToySAE(nn.Module):
W_enc: Float[Tensor, "inst d_in d_sae"]
_W_dec: Float[Tensor, "inst d_sae d_in"] | None
b_enc: Float[Tensor, "inst d_sae"]
b_dec: Float[Tensor, "inst d_in"]
def __init__(self, cfg: ToySAEConfig, model: ToyModel) -> None:
super(ToySAE, self).__init__()
assert cfg.d_in == model.cfg.d_hidden, "Model's hidden dim doesn't match SAE input dim"
self.cfg = cfg
self.model = model.requires_grad_(False)
self.model.W.data[1:] = self.model.W.data[0]
self.model.b_final.data[1:] = self.model.b_final.data[0]
raise NotImplementedError()
self.to(device)
@property
def W_dec(self) -> Float[Tensor, "inst d_sae d_in"]:
return self._W_dec if self._W_dec is not None else self.W_enc.transpose(-1, -2)
@property
def W_dec_normalized(self) -> Float[Tensor, "inst d_sae d_in"]:
"""
Returns decoder weights, normalized over the autoencoder input dimension.
"""
# You'll fill this in later
raise NotImplementedError()
def generate_batch(self, batch_size: int) -> Float[Tensor, "batch inst d_in"]:
"""
Generates a batch of hidden activations from our model.
"""
# You'll fill this in later
raise NotImplementedError()
def forward(
self, h: Float[Tensor, "batch inst d_in"]
) -> tuple[
dict[str, Float[Tensor, "batch inst"]],
Float[Tensor, "batch inst"],
Float[Tensor, "batch inst d_sae"],
Float[Tensor, "batch inst d_in"],
]:
"""
Forward pass on the autoencoder.
Args:
h: hidden layer activations of model
Returns:
loss_dict: dict of different loss terms, each having shape (batch_size, n_inst)
loss: total loss (i.e. sum over terms of loss dict), same shape as loss terms
acts_post: autoencoder latent activations, after applying ReLU
h_reconstructed: reconstructed autoencoder input
"""
# You'll fill this in later
raise NotImplementedError()
def optimize(
self,
batch_size: int = 1024,
steps: int = 10_000,
log_freq: int = 100,
lr: float = 1e-3,
lr_scale: Callable[[int, int], float] = constant_lr,
resample_method: Literal["simple", "advanced", None] = None,
resample_freq: int = 2500,
resample_window: int = 500,
resample_scale: float = 0.5,
hidden_sample_size: int = 256,
) -> list[dict[str, Any]]:
"""
Optimizes the autoencoder using the given hyperparameters.
Args:
model: we reconstruct features from model's hidden activations
batch_size: size of batches we pass through model & train autoencoder on
steps: number of optimization steps
log_freq: number of optimization steps between logging
lr: learning rate
lr_scale: learning rate scaling function
resample_method: method for resampling dead latents
resample_freq: number of optimization steps between resampling dead latents
resample_window: number of steps needed for us to classify a neuron as dead
resample_scale: scale factor for resampled neurons
hidden_sample_size: size of hidden value sample we add to the logs (for visualization)
Returns:
data_log: dictionary containing data we'll use for visualization
"""
assert resample_window <= resample_freq
optimizer = t.optim.Adam(self.parameters(), lr=lr) # betas=(0.0, 0.999)
frac_active_list = []
progress_bar = tqdm(range(steps))
# Create lists of dicts to store data we'll eventually be plotting
data_log = []
for step in progress_bar:
# Resample dead latents
if (resample_method is not None) and ((step + 1) % resample_freq == 0):
frac_active_in_window = t.stack(frac_active_list[-resample_window:], dim=0)
if resample_method == "simple":
self.resample_simple(frac_active_in_window, resample_scale)
elif resample_method == "advanced":
self.resample_advanced(frac_active_in_window, resample_scale, batch_size)
# Update learning rate
step_lr = lr * lr_scale(step, steps)
for group in optimizer.param_groups:
group["lr"] = step_lr
# Get a batch of hidden activations from the model
with t.inference_mode():
h = self.generate_batch(batch_size)
# Optimize
loss_dict, loss, acts, _ = self.forward(h)
loss.mean(0).sum().backward()
optimizer.step()
optimizer.zero_grad()
# Normalize decoder weights by modifying them directly (if not using tied weights)
if not self.cfg.tied_weights:
self.W_dec.data = self.W_dec_normalized.data
# Calculate the mean sparsities over batch dim for each feature
frac_active = (acts.abs() > 1e-8).float().mean(0)
frac_active_list.append(frac_active)
# Display progress bar, and log a bunch of values for creating plots / animations
if step % log_freq == 0 or (step + 1 == steps):
progress_bar.set_postfix(
lr=step_lr,
loss=loss.mean(0).sum().item(),
frac_active=frac_active.mean().item(),
**{k: v.mean(0).sum().item() for k, v in loss_dict.items()}, # type: ignore
)
with t.inference_mode():
loss_dict, loss, acts, h_r = self.forward(
h := self.generate_batch(hidden_sample_size)
)
data_log.append(
{
"steps": step,
"frac_active": (acts.abs() > 1e-8).float().mean(0).detach().cpu(),
"loss": loss.detach().cpu(),
"h": h.detach().cpu(),
"h_r": h_r.detach().cpu(),
**{name: param.detach().cpu() for name, param in self.named_parameters()},
**{name: loss_term.detach().cpu() for name, loss_term in loss_dict.items()},
}
)
return data_log
@t.no_grad()
def resample_simple(
self,
frac_active_in_window: Float[Tensor, "window inst d_sae"],
resample_scale: float,
) -> None:
"""
Resamples dead latents, by modifying the model's weights and biases inplace.
Resampling method is:
- For each dead neuron, generate a random vector of size (d_in,), and normalize these vecs
- Set new values of W_dec and W_enc to be these normalized vecs, at each dead neuron
- Set b_enc to be zero, at each dead neuron
"""
raise NotImplementedError()
@t.no_grad()
def resample_advanced(
self,
frac_active_in_window: Float[Tensor, "window inst d_sae"],
resample_scale: float,
batch_size: int,
) -> None:
"""
Resamples latents that have been dead for `dead_feature_window` steps, according to `frac_active`.
Resampling method is:
- Compute the L2 reconstruction loss produced from the hidden state vecs `h`
- Randomly choose values of `h` with probability proportional to their reconstruction loss
- Set new values of W_dec & W_enc to be these centered & normalized vecs, at each dead neuron
- Set b_enc to be zero, at each dead neuron
"""
raise NotImplementedError()
Exercise - implement __init__
Difficulty:
🔴⚪⚪⚪⚪
Importance:
🔵🔵🔵⚪⚪
You should spend up to 5-15 minutes on this exercise.
You should implement the __init__ method below. This should define the weights b_enc, b_dec, W_enc and _W_dec. Use Kaiming uniform for weight initialization, and initialize the biases at zero.
Note, we use _W_dec to handle the case of tied weights: it should be None if we have tied weights, and a proper parameter if we don't have tied weights. The property W_dec we've given you in the class above will deal with both cases for you.
Why might we want / not want to tie our weights?
In our Model implementations, we used a weight and its transpose. You might think it also makes sense to have the encoder and decoder weights be transposed copies of each other, since intuitively both the encoder and decoder's latent vectors meant to represent some feature's "direction in the original model's hidden dimension".
The reason we might not want to tie weights is pretty subtle. The job of the encoder is in some sense to recover features from superposition, whereas the job of the decoder is just to represent that feature faithfully if present (since the goal of our SAE is to write the input as a linear combination of W_dec vectors) - this is why we generally see the decoder weights as the "true direction" for a feature, when weights are untied.
The diagram below might help illustrate this concept (if you want, you can replicate the results in this diagram using our toy model setup!).
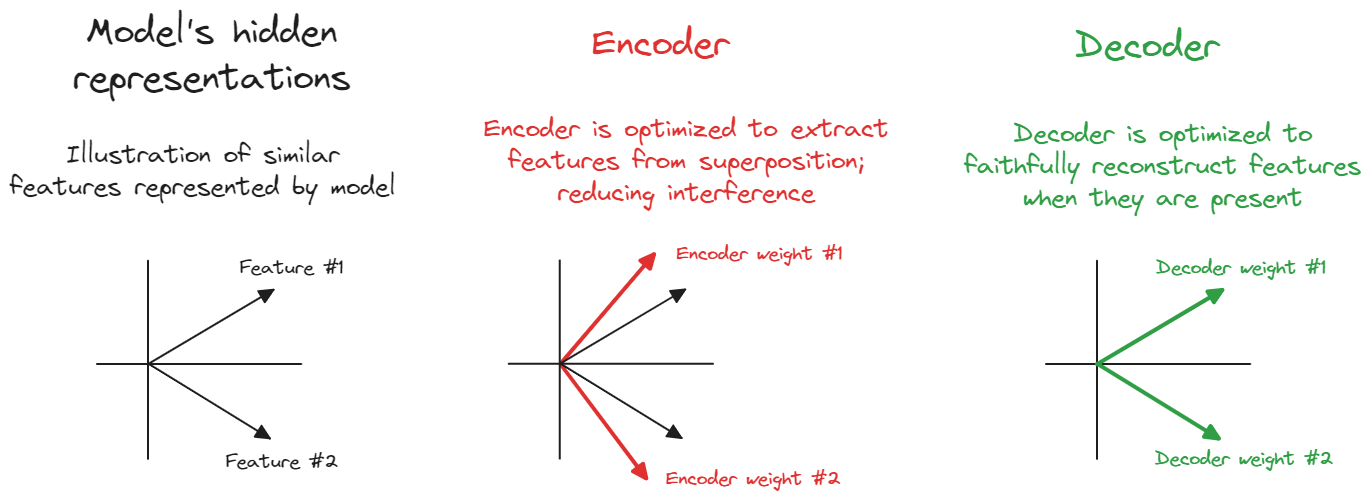
In simple settings like this toy model we might not benefit much from untying weights, and tying weights can actually help us avoid finding annoying local minima in our optimization. However, for most of these exercises we'll use untied weights in order to illustrate SAE concepts more clearly.
Also, note that we've defined self.cfg and self.model for you in the init function - in the latter case, we've frozen the model's weights (because when you train your SAE you don't want to track gradients in your base model), and we've also modified the model's weights so they all match the first instance (this is so we can more easily interpret our SAE plots we'll create when we finish training).
# Go back up and edit your `ToySAE.__init__` method, then run the test below
tests.test_sae_init(ToySAE)
Solution
def __init__(self: ToySAE, cfg: ToySAEConfig, model: ToyModel) -> None:
super(ToySAE, self).__init__()
assert cfg.d_in == model.cfg.d_hidden, "Model's hidden dim doesn't match SAE input dim"
self.cfg = cfg
self.model = model.requires_grad_(False)
self.model.W.data[1:] = self.model.W.data[0]
self.model.b_final.data[1:] = self.model.b_final.data[0]
self.W_enc = nn.Parameter(nn.init.kaiming_uniform_(t.empty((cfg.n_inst, cfg.d_in, cfg.d_sae))))
self._W_dec = (
None
if self.cfg.tied_weights
else nn.Parameter(nn.init.kaiming_uniform_(t.empty((cfg.n_inst, cfg.d_sae, cfg.d_in))))
)
self.b_enc = nn.Parameter(t.zeros(cfg.n_inst, cfg.d_sae))
self.b_dec = nn.Parameter(t.zeros(cfg.n_inst, cfg.d_in))
self.to(device)
ToySAE.__init__ = __init__
Exercise - implement W_dec_normalized
Difficulty:
🔴⚪⚪⚪⚪
Importance:
🔵🔵🔵⚪⚪
You should spend 5-10 minutes on this exercise.
You should now fill in the W_dec_normalized property, which returns the decoder weights, normalized (with L2 norm) over the autoencoder input dimension. Note that the existence of the W_dec property means you can safety refer to this attribute, without having to worry about _W_dec any more. Also, remember to add cfg.weight_normalize_eps to your denominator (this helps avoid divide-by-zero errors).
Why do we need W_dec_normalized?
We normalize W_dec to stop the model from cheating! Imagine if we didn't normalize W_dec - the model could make W_enc 10 times smaller, and make W_dec 10 times larger. The outputs would be the same (keeping the reconstruction error constant), but the latent activations would be 10 times smaller, letting the model shrink the sparsity penalty (the L1 loss term) without learning anything useful.
L2-normalizing the columns of W_dec also makes the magnitude of our latent activations more clearly interpretable: with normalization, they answer the question "how much of each unit-length feature is present?"
# Go back up and edit your `ToySAE.W_dec_normalized` method, then run the test below
tests.test_sae_W_dec_normalized(ToySAE)
Solution
@property
def W_dec_normalized(self: ToySAE) -> Float[Tensor, "inst d_sae d_in"]:
"""Returns decoder weights, normalized over the autoencoder input dimension."""
return self.W_dec / (self.W_dec.norm(dim=-1, keepdim=True) + self.cfg.weight_normalize_eps)
ToySAE.W_dec_normalized = W_dec_normalized
Exercise - implement generate_batch
Difficulty:
🔴🔴⚪⚪⚪
Importance:
🔵🔵🔵⚪⚪
You should spend 5-15 minutes on this exercise.
As mentioned, our data no longer comes directly from ToyModel.generate_batch. Instead, we use Model.generate_batch to get our model input $x$, and then apply our model's W matrix to get its hidden activations $h=Wx$. Note that we're working with the model from the "Superposition in a Nonprivileged Basis" model, meaning there's no ReLU function to apply to get $h$.
You should fill in the generate_batch method now, then run the test. Note - remember to use self.model rather than model!
# Go back up and edit your `ToySAE.generate_batch` method, then run the test below
tests.test_sae_generate_batch(ToySAE)
Solution
def generate_batch(self: ToySAE, batch_size: int) -> Float[Tensor, "batch inst d_in"]:
"""
Generates a batch of hidden activations from our model.
"""
return einops.einsum(
self.model.generate_batch(batch_size),
self.model.W,
"batch inst feats, inst d_in feats -> batch inst d_in",
)
ToySAE.generate_batch = generate_batch
Exercise - implement forward
Difficulty:
🔴🔴🔴⚪⚪
Importance:
🔵🔵🔵🔵🔵
You should spend up to 25-40 minutes on this exercise.
You should calculate the autoencoder's hidden state activations as $z = \operatorname{ReLU}(W_{enc}(h - b_{dec}) + b_{enc})$, and then reconstruct the output as $h' = W_{dec}z + b_{dec}$. A few notes:
- The first variable we return is a
loss_dict, which contains the loss tensors of shape (batch_size, n_inst) for both terms in our loss function (before multiplying by the L1 coefficient). This is used for logging, and it'll also be used later in our neuron resampling methods. For this architecture, your keys should be "L_reconstruction" and "L_sparsity".
- The second variable we return is the
loss term, which also has shape (batch_size, n_inst), and is created by summing the losses in loss_dict (with sparsity loss multiplied by cfg.sparsity_coeff). When doing gradient descent, we'll average over the batch dimension & sum over the instance dimension (since we're training our instances independently & in parallel).
- The third variable we return is the hidden state activations
acts, which are also used later for neuron resampling (as well as logging how many latents are active).
- The fourth variable we return is the reconstructed hidden states
h_reconstructed, i.e. the autoencoder's actual output.
An important note regarding our loss term - the reconstruction loss is the squared difference between input & output averaged over the d_in dimension, but the sparsity penalty is the L1 norm of the hidden activations summed over the d_sae dimension. Can you see why we average one but sum the other?
Hint
Suppose we averaged L1 loss too. Consider the gradients a single latent receives from the reconstruction loss and sparsity penalty - what do they look like in the limit of very large d_sae?
Answer - why we average L2 loss over d_in but sum L1 loss over d_sae
Suppose for sake of argument we averaged L1 loss too. Imagine if we doubled the latent dimension, but kept all other SAE hyperparameters the same. The per-hidden-unit gradient from the reconstruction loss would still be the same (because changing a single hidden unit's encoder or decoder vector would have the same effect on the output as before), but the per-hidden-unit gradient from the sparsity penalty would have halved (because we're averaging the sparsity penalty over d_sae). This means that in the limit, the sparsity penalty wouldn't matter at all, and the only important thing would be getting zero reconstruction loss.
Note - make sure you're using self.W_dec_normalized rather than self.W_dec in your forward function. This is because if we're using tied weights then we won't be able to manually normalize W_dec inplace, but we still want to use the normalized version.
# Go back up and edit your `ToySAE.forward` method, then run the test below
tests.test_sae_forward(ToySAE)
Solution
def forward(
self: ToySAE, h: Float[Tensor, "batch inst d_in"]
) -> tuple[
dict[str, Float[Tensor, "batch inst"]],
Float[Tensor, "batch inst"],
Float[Tensor, "batch inst d_sae"],
Float[Tensor, "batch inst d_in"],
]:
"""
Forward pass on the autoencoder.
Args:
h: hidden layer activations of model
Returns:
loss_dict: dict of different loss terms, each dict value having shape (batch_size, n_inst)
loss: total loss (i.e. sum over terms of loss dict), same shape as loss_dict values
acts_post: autoencoder latent activations, after applying ReLU
h_reconstructed: reconstructed autoencoder input
"""
h_cent = h - self.b_dec
# Compute latent (hidden layer) activations
acts_pre = (
einops.einsum(h_cent, self.W_enc, "batch inst d_in, inst d_in d_sae -> batch inst d_sae")
+ self.b_enc
)
acts_post = F.relu(acts_pre)
# Compute reconstructed input
h_reconstructed = (
einops.einsum(
acts_post, self.W_dec_normalized, "batch inst d_sae, inst d_sae d_in -> batch inst d_in"
)
+ self.b_dec
)
# Compute loss terms
L_reconstruction = (h_reconstructed - h).pow(2).mean(-1)
L_sparsity = acts_post.abs().sum(-1)
loss_dict = {"L_reconstruction": L_reconstruction, "L_sparsity": L_sparsity}
loss = L_reconstruction + self.cfg.sparsity_coeff * L_sparsity
return loss_dict, loss, acts_post, h_reconstructed
ToySAE.forward = forward
Training your SAE
The optimize method has been given to you. A few notes on how it differs from your previous model:
- Before each optimization step, we implement neuron resampling - we'll get to this later.
- We have more logging, via the
data_log dictionary - we'll use this for visualization.
- We've used
betas=(0.0, 0.999), to match the description in Anthropic's Feb 2024 update - although they document it to work better specifically for large models, we may as well match it here.
First, let's define and train our model, and visualize model weights and the data returned from sae.generate_batch (which are the hidden state representations of our trained model, and will be used for training our SAE).
Note that we'll use a feature probability of 2.5% (and assume independence between features) for all subsequent exercises.
d_hidden = d_in = 2
n_features = d_sae = 5
n_inst = 16
# Create a toy model, and train it to convergence
cfg = ToyModelConfig(n_inst=n_inst, n_features=n_features, d_hidden=d_hidden)
model = ToyModel(cfg=cfg, device=device, feature_probability=0.025)
model.optimize()
sae = ToySAE(cfg=ToySAEConfig(n_inst=n_inst, d_in=d_in, d_sae=d_sae), model=model)
h = sae.generate_batch(512)
utils.plot_features_in_2d(model.W[:8], title="Base model")
utils.plot_features_in_2d(
einops.rearrange(h[:, :8], "batch inst d_in -> inst d_in batch"),
title="Hidden state representation of a random batch of data",
)
Now, let's train our SAE, and visualize the instances with lowest loss! We've also created a function animate_features_in_2d which creates an animation of the training over time. If the inline displaying doesn't work, you might have to open the saved HTML file in your browser to see it.
data_log = sae.optimize(steps=20_000)
utils.animate_features_in_2d(
data_log,
instances=list(range(8)), # only plot the first 8 instances
rows=["W_enc", "_W_dec"],
filename=str(section_dir / "animation-training.html"),
title="SAE on toy model",
)
# If this display code doesn't work, try saving & opening animation in your browser
with open(section_dir / "animation-training.html") as f:
display(HTML(f.read()))
Click to see the expected output


