4️⃣ Path Patching

Learning Objectives

• Understand the idea of path patching, and how it differs from activation patching
• Implement path patching from scratch (i.e. using hooks)
• Replicate several of the results in the IOI paper

This section will be a lot less conceptual and exploratory than the last two sections, and a lot more technical and rigorous. You'll learn what path patching is and how it works, and you'll use it to replicate many of the paper's results (as well as some other paper results not related to path patching).

Setup

Here, we'll be more closely following the setup that the paper's authors used, rather than the rough-and-ready exploration we used in the first few sections. To be clear, a lot of the rigour that we'll be using in the setup here isn't necessary if you're just starting to investigate a model's circuit. This rigour is necessary if you're publishing a paper, but it can take a lot of time and effort!

from part41_indirect_object_identification.ioi_dataset import NAMES, IOIDataset

The dataset we'll be using is an instance of IOIDataset, which is generated by randomly choosing names from the NAMES list (as well as sentence templates and objects from different lists). You can look at the ioi_dataset.py file to see details of how this is done.

(Note - you can reduce N if you're getting memory errors from running this code. If you're still getting memory errors from N = 10 then you're recommended to switch to Colab, or to use a virtual machine e.g. via Lambda Labs.)

N = 25
ioi_dataset = IOIDataset(
    prompt_type="mixed",
    N=N,
    tokenizer=model.tokenizer,
    prepend_bos=False,
    seed=1,
    device=str(device),
)

This dataset has a few useful attributes & methods. Here are the main ones you should be aware of for these exercises:

• toks is a tensor of shape (batch_size, max_seq_len) containing the token IDs (i.e. this is what you pass to your model)
• s_tokenIDs and io_tokenIDs are lists containing the token IDs for the subjects and objects
• sentences is a list containing the sentences (as strings)
• word_idx is a dictionary mapping word types (e.g. "S1", "S2", "IO" or "end") to tensors containing the positions of those words for each sequence in the dataset.
  • This is particularly handy for indexing, since the positions of the subject, indirect object, and end tokens are no longer the same in every sentence like they were in previous sections.

Firstly, what dataset should we use for patching? In the previous section we just flipped the subject and indirect object tokens around, which meant the direction of the signal was flipped around. However, what we'll be doing here is a bit more principled - rather than flipping the IOI signal, we'll be erasing it. We do this by constructing a new dataset from ioi_dataset which replaces every name with a different random name. This way, the sentence structure stays the same, but all information related to the actual indirect object identification task (i.e. the identities and positions of repeated names) has been erased.

For instance, given the sentence "When John and Mary went to the shops, John gave the bag to Mary", the corresponding sentence in the ABC dataset might be "When Edward and Laura went to the shops, Adam gave the bag to Mary". We would expect the residual stream for the latter prompt to carry no token or positional information which could help it solve the IOI task (i.e. favouring Mary over John, or favouring the 2nd token over the 4th token).

We define this dataset below. Note the syntax of the gen_flipped_prompts method - the letters tell us how to replace the names in the sequence. For instance, ABB->XYZ tells us to take sentences of the form "When Mary and John went to the store, John gave a drink to Mary" with "When [X] and [Y] went to the store, [Z] gave a drink to Mary" for 3 independent randomly chosen names [X], [Y] and [Z]. We'll use this function more in the bonus section, when we're trying to disentangle positional and token signals (since we can also do fun things like ABB->BAB to swap the first two names, etc).

abc_dataset = ioi_dataset.gen_flipped_prompts("ABB->XYZ, BAB->XYZ")

Let's take a look at this dataset. We'll define a helper function make_table, which prints out tables after being fed columns rather than rows (don't worry about the syntax, it's not important).

def format_prompt(sentence: str) -> str:
    """Format a prompt by underlining names (for rich print)"""
    return (
        re.sub(
            "(" + "|".join(NAMES) + ")", lambda x: f"[u bold dark_orange]{x.group(0)}[/]", sentence
        )
        + "\n"
    )


def make_table(cols, colnames, title="", n_rows=5, decimals=4):
    """Makes and displays a table, from cols rather than rows (using rich print)"""
    table = Table(*colnames, title=title)
    rows = list(zip(*cols))
    f = lambda x: x if isinstance(x, str) else f"{x:.{decimals}f}"
    for row in rows[:n_rows]:
        table.add_row(*list(map(f, row)))
    rprint(table)


make_table(
    colnames=["IOI prompt", "IOI subj", "IOI indirect obj", "ABC prompt"],
    cols=[
        map(format_prompt, ioi_dataset.sentences),
        model.to_string(ioi_dataset.s_tokenIDs).split(),
        model.to_string(ioi_dataset.io_tokenIDs).split(),
        map(format_prompt, abc_dataset.sentences),
    ],
    title="Sentences from IOI vs ABC distribution",
)

                                      Sentences from IOI vs ABC distribution                                       
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ IOI prompt                              ┃ IOI subj ┃ IOI indirect obj ┃ ABC prompt                              ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│ When Victoria and Jane got a snack at   │ Jane     │ Victoria         │ When Alan and Sullivan got a snack at   │
│ the store, Jane decided to give it to   │          │                  │ the store, Adam decided to give it to   │
│ Victoria                                │          │                  │ Victoria                                │
│                                         │          │                  │                                         │
│ When Sullivan and Rose got a necklace   │ Sullivan │ Rose             │ When Marcus and Max got a necklace at   │
│ at the garden, Sullivan decided to give │          │                  │ the garden, Jeremy decided to give it   │
│ it to Rose                              │          │                  │ to Rose                                 │
│                                         │          │                  │                                         │
│ When Alan and Alex got a drink at the   │ Alex     │ Alan             │ When Jay and Jason got a drink at the   │
│ store, Alex decided to give it to Alan  │          │                  │ store, Jacob decided to give it to Alan │
│                                         │          │                  │                                         │
│ Then, Jessica and Crystal had a long    │ Jessica  │ Crystal          │ Then, Joshua and Jack had a long        │
│ argument, and afterwards Jessica said   │          │                  │ argument, and afterwards Grant said to  │
│ to Crystal                              │          │                  │ Crystal                                 │
│                                         │          │                  │                                         │
│ Then, Jonathan and Kevin were working   │ Kevin    │ Jonathan         │ Then, Alice and Mark were working at    │
│ at the school. Kevin decided to give a  │          │                  │ the school. Carter decided to give a    │
│ necklace to Jonathan                    │          │                  │ necklace to Jonathan                    │
│                                         │          │                  │                                         │
└─────────────────────────────────────────┴──────────┴──────────────────┴─────────────────────────────────────────┘

Next, we'll define functions similar to the ones from previous sections. We've just given you these, rather than making you repeat the exercise of writing them (although you should compare these functions to the ones you wrote earlier, and make sure you understand how they work).

We'll call these functions something slightly different, so as not to pollute namespace.

def logits_to_ave_logit_diff_2(
    logits: Float[Tensor, "batch seq d_vocab"],
    ioi_dataset: IOIDataset = ioi_dataset,
    per_prompt=False,
) -> Float[Tensor, "*batch"]:
    """
    Returns logit difference between the correct and incorrect answer.

    If per_prompt=True, return the array of differences rather than the average.
    """
    # Only the final logits are relevant for the answer
    # Get the logits corresponding to the indirect object / subject tokens respectively
    io_logits: Float[Tensor, "batch"] = logits[
        range(logits.size(0)), ioi_dataset.word_idx["end"], ioi_dataset.io_tokenIDs
    ]
    s_logits: Float[Tensor, "batch"] = logits[
        range(logits.size(0)), ioi_dataset.word_idx["end"], ioi_dataset.s_tokenIDs
    ]
    # Find logit difference
    answer_logit_diff = io_logits - s_logits
    return answer_logit_diff if per_prompt else answer_logit_diff.mean()


model.reset_hooks(including_permanent=True)

ioi_logits_original, ioi_cache = model.run_with_cache(ioi_dataset.toks)
abc_logits_original, abc_cache = model.run_with_cache(abc_dataset.toks)

ioi_per_prompt_diff = logits_to_ave_logit_diff_2(ioi_logits_original, per_prompt=True)
abc_per_prompt_diff = logits_to_ave_logit_diff_2(abc_logits_original, per_prompt=True)

ioi_average_logit_diff = logits_to_ave_logit_diff_2(ioi_logits_original).item()
abc_average_logit_diff = logits_to_ave_logit_diff_2(abc_logits_original).item()

print(f"Average logit diff (IOI dataset): {ioi_average_logit_diff:.4f}")
print(f"Average logit diff (ABC dataset): {abc_average_logit_diff:.4f}")

make_table(
    colnames=["IOI prompt", "IOI logit diff", "ABC prompt", "ABC logit diff"],
    cols=[
        map(format_prompt, ioi_dataset.sentences),
        ioi_per_prompt_diff,
        map(format_prompt, abc_dataset.sentences),
        abc_per_prompt_diff,
    ],
    title="Sentences from IOI vs ABC distribution",
)

Average logit diff (IOI dataset): 2.8052
Average logit diff (ABC dataset): -0.7699

                                      Sentences from IOI vs ABC distribution                                       
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━┓
┃ IOI prompt                            ┃ IOI logit diff ┃ ABC prompt                            ┃ ABC logit diff ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━┩
│ When Victoria and Jane got a snack at │ 2.4403         │ When Alan and Sullivan got a snack at │ -2.4177        │
│ the store, Jane decided to give it to │                │ the store, Adam decided to give it to │                │
│ Victoria                              │                │ Victoria                              │                │
│                                       │                │                                       │                │
│ When Sullivan and Rose got a necklace │ 6.5408         │ When Marcus and Max got a necklace at │ 6.1583         │
│ at the garden, Sullivan decided to    │                │ the garden, Jeremy decided to give it │                │
│ give it to Rose                       │                │ to Rose                               │                │
│                                       │                │                                       │                │
│ When Alan and Alex got a drink at the │ 3.3345         │ When Jay and Jason got a drink at the │ -1.7351        │
│ store, Alex decided to give it to     │                │ store, Jacob decided to give it to    │                │
│ Alan                                  │                │ Alan                                  │                │
│                                       │                │                                       │                │
│ Then, Jessica and Crystal had a long  │ 1.1972         │ Then, Joshua and Jack had a long      │ -4.2358        │
│ argument, and afterwards Jessica said │                │ argument, and afterwards Grant said   │                │
│ to Crystal                            │                │ to Crystal                            │                │
│                                       │                │                                       │                │
│ Then, Jonathan and Kevin were working │ 3.0530         │ Then, Alice and Mark were working at  │ 0.1968         │
│ at the school. Kevin decided to give  │                │ the school. Carter decided to give a  │                │
│ a necklace to Jonathan                │                │ necklace to Jonathan                  │                │
│                                       │                │                                       │                │
└───────────────────────────────────────┴────────────────┴───────────────────────────────────────┴────────────────┘

Note that we're always measuring performance with respect to the correct answers for the IOI dataset, not the ABC dataset, because we want our ABC dataset to carry no information that helps with the IOI task (hence patching it in gives us signals which are totally uncorrelated with the correct answer). For instance, the model will obviously not complete sentences like "When Max and Victoria got a snack at the store, Clark decided to give it to" with the name "Tyler".

Finally, let's define a new ioi_metric function which works for our new data.

In order to match the paper's results, we'll use a different convention here. 0 means performance is the same as on the IOI dataset (i.e. hasn't been harmed in any way), and -1 means performance is the same as on the ABC dataset (i.e. the model has completely lost the ability to distinguish between the subject and indirect object).

Again, we'll call this function something slightly different.

def ioi_metric_2(
    logits: Float[Tensor, "batch seq d_vocab"],
    clean_logit_diff: float = ioi_average_logit_diff,
    corrupted_logit_diff: float = abc_average_logit_diff,
    ioi_dataset: IOIDataset = ioi_dataset,
) -> float:
    """
    We calibrate this so that the value is 0 when performance isn't harmed (i.e. same as IOI
    dataset), and -1 when performance has been destroyed (i.e. is same as ABC dataset).
    """
    patched_logit_diff = logits_to_ave_logit_diff_2(logits, ioi_dataset)
    return (patched_logit_diff - clean_logit_diff) / (clean_logit_diff - corrupted_logit_diff)


print(f"IOI metric (IOI dataset): {ioi_metric_2(ioi_logits_original):.4f}")
print(f"IOI metric (ABC dataset): {ioi_metric_2(abc_logits_original):.4f}")

What is path patching?

In the previous section, we looked at activation patching, which answers questions like what would happen if you took an attention head, and swapped the value it writes to the residual stream with the value it would have written under a different distribution, while keeping everything else the same?. This proved to be a good way to examine the role of individual components like attention heads, and it allowed us to perform some more subtle analysis like patching keys / queries / values in turn to figure out which of them were more important for which heads.

However, when we're studying a circuit, rather than just swapping out an entire attention head, we might want to ask more nuanced questions like what would happen if the direct input from attention head $A$ to head $B$ (where $B$ comes after $A$) was swapped out with the value it would have been under a different distribution, while keeping everything else the same?. Rather than answering the general question of how important attention heads are, this answers the more specific question of how important the circuit formed by connecting up these two attention heads is. Path patching is designed to answer questions like these.

The following diagrams might help explain the difference between activation and path patching in transformers. Recall that activation patching looked like:

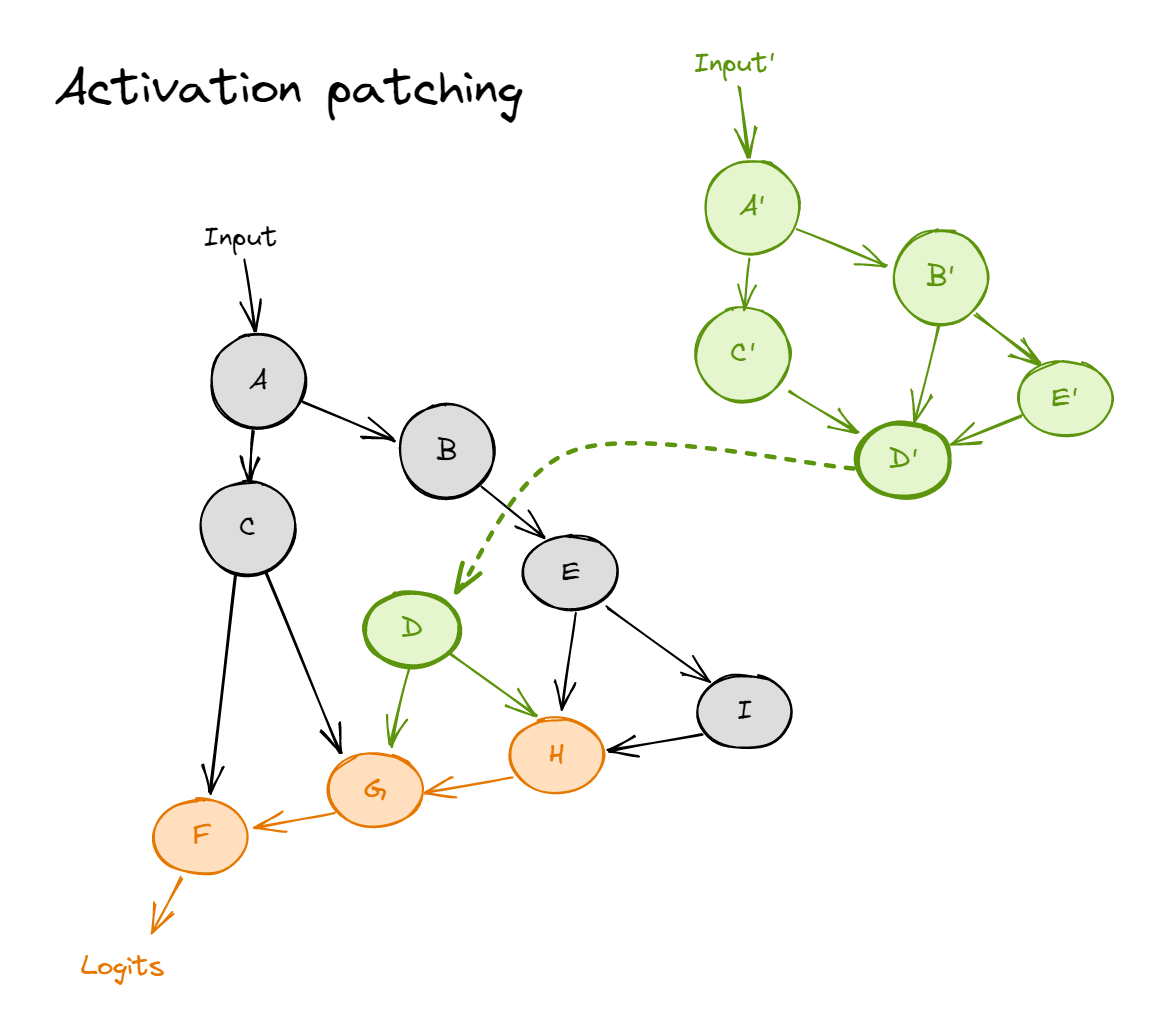
where the black and green distributions are our clean and corrupted datasets respectively (so this would be ioi_dataset and abc_dataset). In contrast, path patching involves replacing edges rather than nodes. In the diagram below, we're replacing the edge $D \to G$ with what it would be on the corrupted distribution. So in our patched run, $G$ is calculated just like it would be on the clean distribution, but as if the direct input from $D$ had come from the corrupted distribution instead.

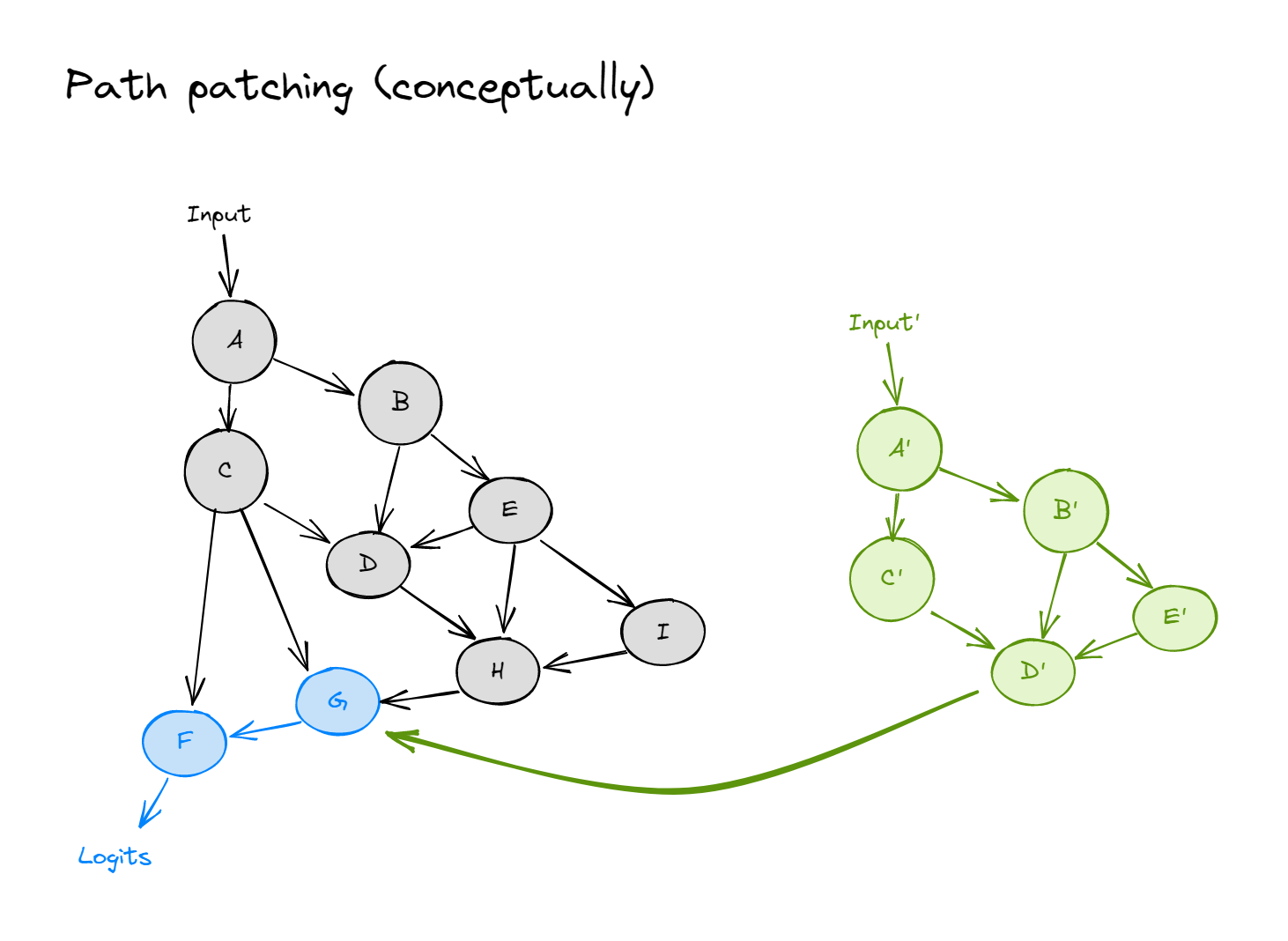
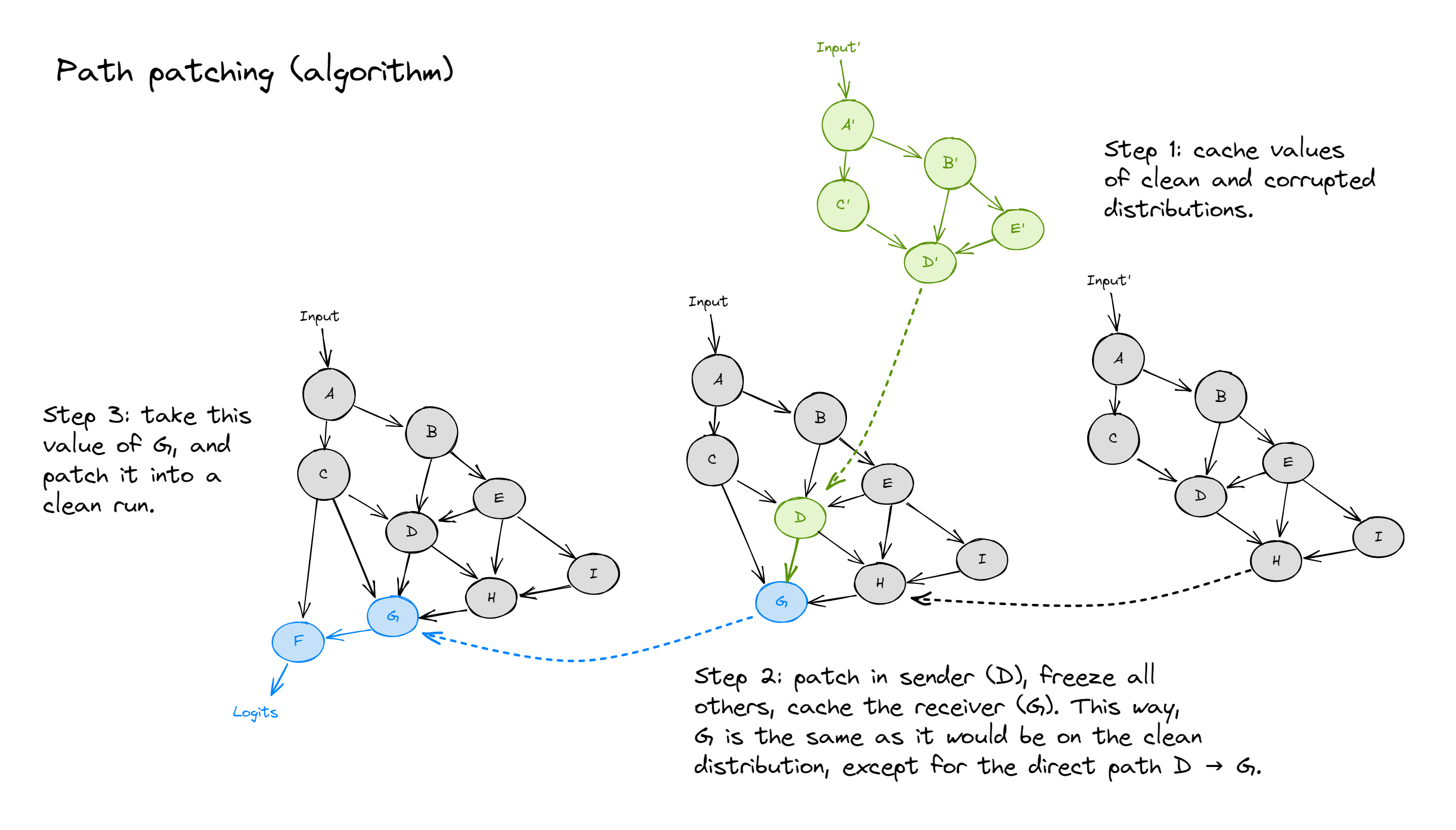
Unfortunately, for a transformer, this is easier to describe than to actually implement. This is because the "nodes" are attention heads, and the "edges" are all tangled together in the residual stream (that is to say, it's not clear how one could change the value of one edge without without affecting every path that includes that edge). The solution is to use the 3-step algorithm shown in the diagram below (which reads from right to left).

Terminology note - we call head $D$ the sender node, and head $G$ the receiver node. Also, by "freezing" nodes, we mean "patch with the value that is the same as the input". For instance, if we didn't freeze head $H$ in step 2 below, it would have a different value because it would be affected by the corrupted value of head $D$.

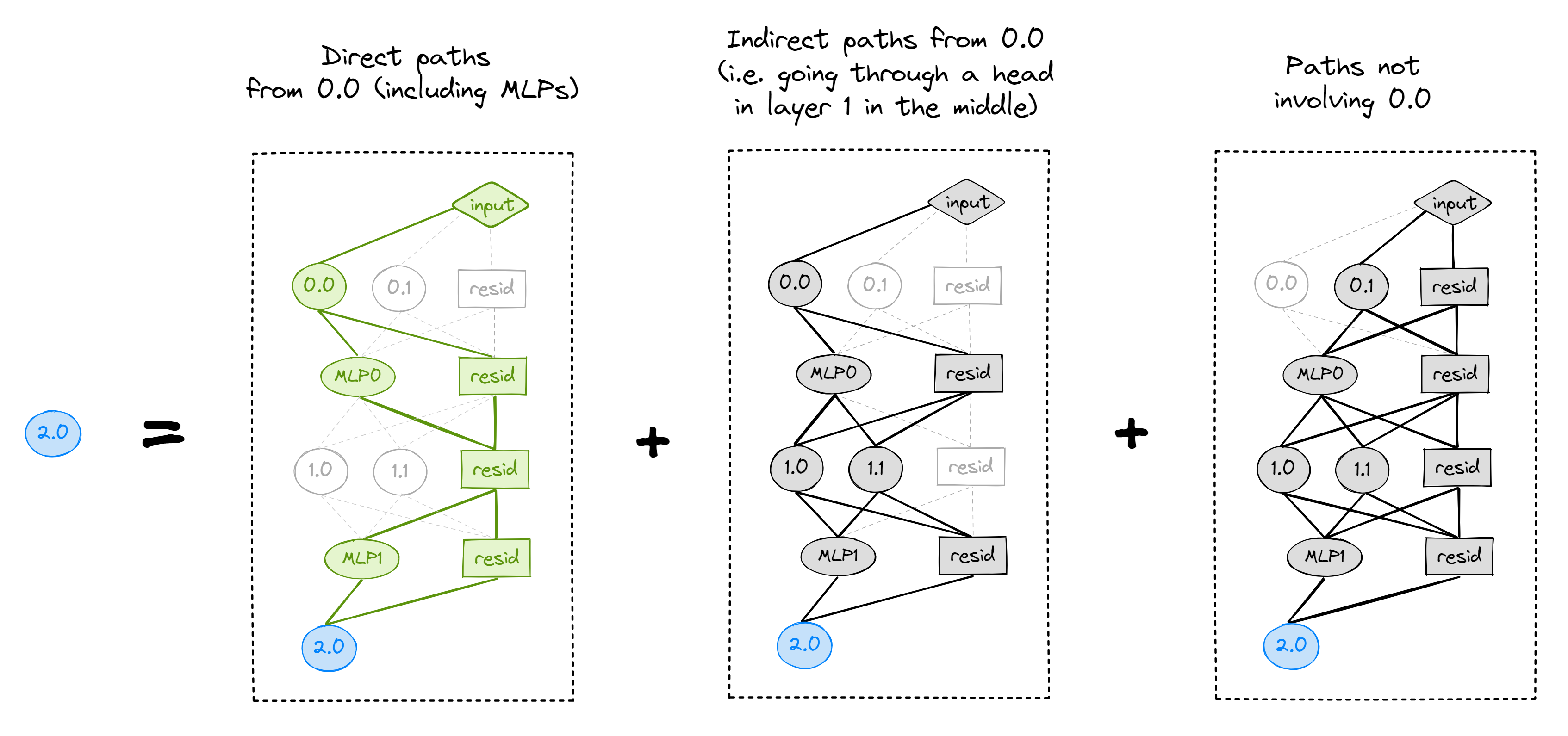
Let's make this concrete, and take a simple 3-layer transformer with 2 heads per layer. Let's perform path patching on the edge from head 0.0 to 2.0 (terminology note: 0.0 is the sender, and 2.0 is the receiver). Note that here, we're considering "direct paths" as anything that doesn't go through another attention head (so it can go through any combination of MLPs). Intuitively, the nodes (attention heads) are the only things that can move information around in the model, and this is the thing we want to study. In contrast, MLPs just perform information processing, and they're not as interesting for this task.

Our 3-step process looks like the diagram below (remember green is corrupted, grey is clean).

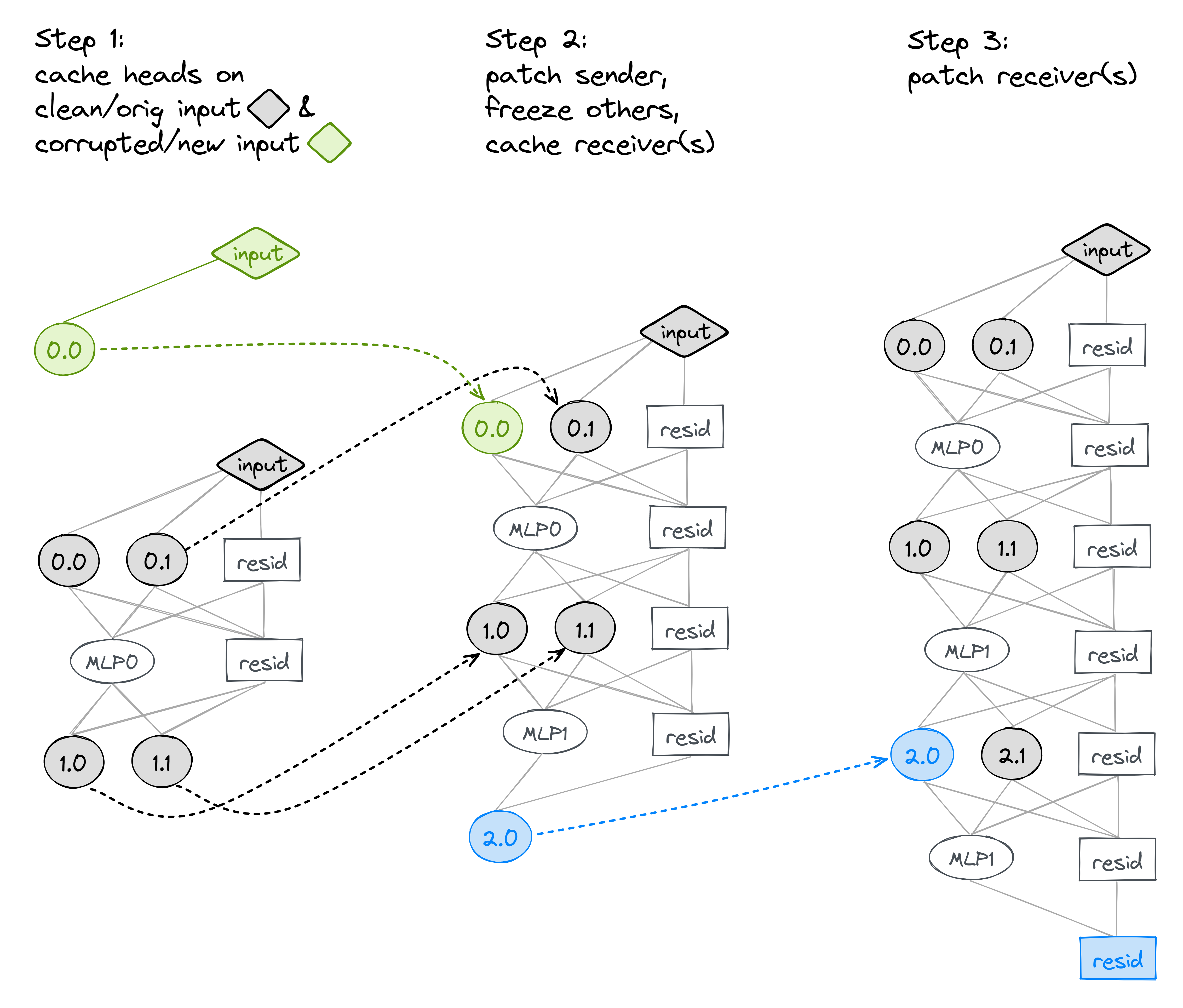
(Note - in this diagram, the uncoloured nodes indicate we aren't doing any patching; we're just allowing them to be computed from the values of nodes which are downstream of it.)

Why does this work? If you stare at the middle picture above for long enough, you'll realise that the contribution from every non-direct path from 0.0 $\to$ 2.0 is the same as it would be on the clean distribution, while all the direct paths' contributions are the same as they would be on the corrupted distribution.

Why MLPs?

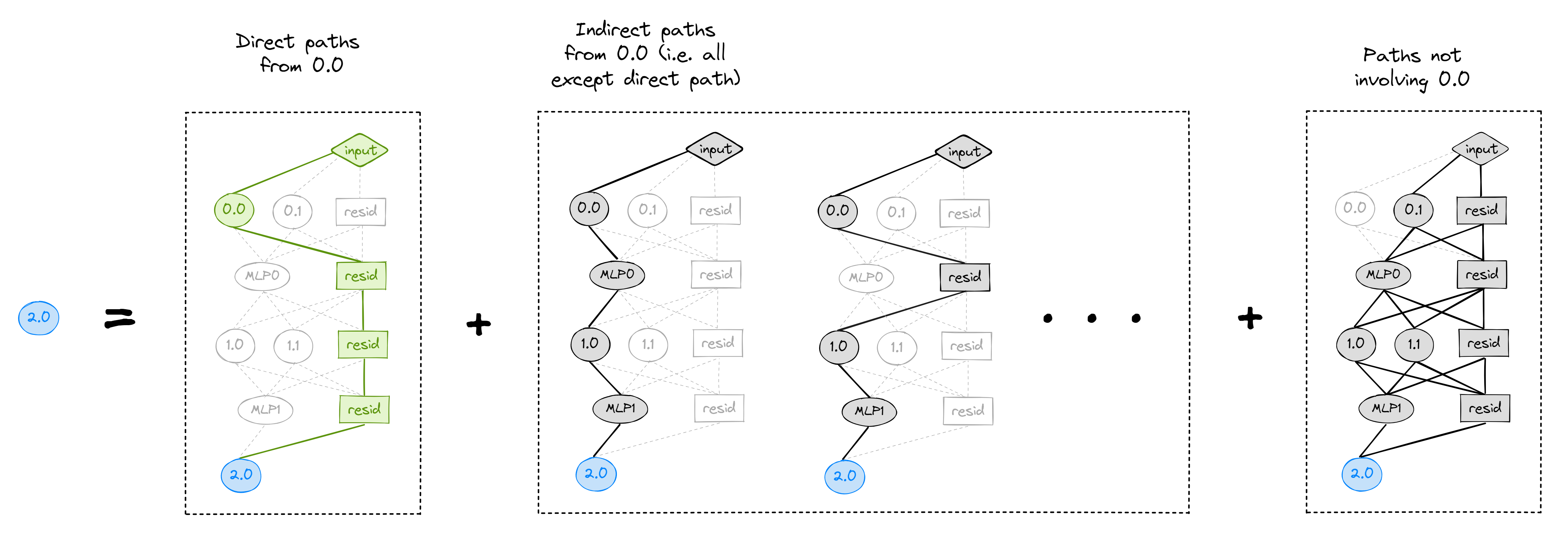
You might be wondering why we're including MLPs as part of our direct path. The short answer is that this is what the IOI paper does, and we're trying to replicate it! The slightly longer answer is that both this method and a method which doesn't count MLPs as the direct path are justifiable.

To take one example, suppose the output of head 0.0 is being used directly by head 2.0, but one of the MLPs is acting as a mediator. To oversimplify, we might imagine that 0.0 writes the vector $v$ into the residual stream, some neuron detects $v$ and writes $w$ to the residual stream, and 2.0 detects $w$. If we didn't count MLPs as a direct path then we wouldn't catch this causal relationship. The drawback is that things get a bit messier, because now we're essentially passing a "fake input" into our MLPs, and it's dangerous to assume that any operation as clean as the one previously described (with vectors $v$, $w$) would still happen under these new circumstances.

Also, having MLPs as part of the direct path doesn't help us understand what role the MLPs play in the circuit, all it does is tell us that some of them are important! Luckily, in the IOI circuit, MLPs aren't important (except for MLP0), and so doing both these forms of path patching get pretty similar results. As an optional exercise, you can reproduce the results from the following few sections using this different form of path patching. It's actually algorithmically easier to implement, because we only need one forward pass rather than two. Can you see why?

Answer

Because the MLPs were part of the direct paths between sender and receiver in the previous version of the algorithm, we had to do a forward pass to find the value we'd be patching into the receivers. But if MLPs aren't part of the direct path, then we can directly compute what to patch into the receiver nodes:

orig_receiver_input <- orig_receiver_input + (new_sender_output - old_sender_output)

Diagram with direct paths not including MLPs:

Path Patching: Name Mover Heads

We'll start with a simple type of path patching - with just one receiver node, which is the final value of the residual stream. We've only discussed receiver nodes being other attention heads so far, but the same priciples hold for any choice of receiver nodes.

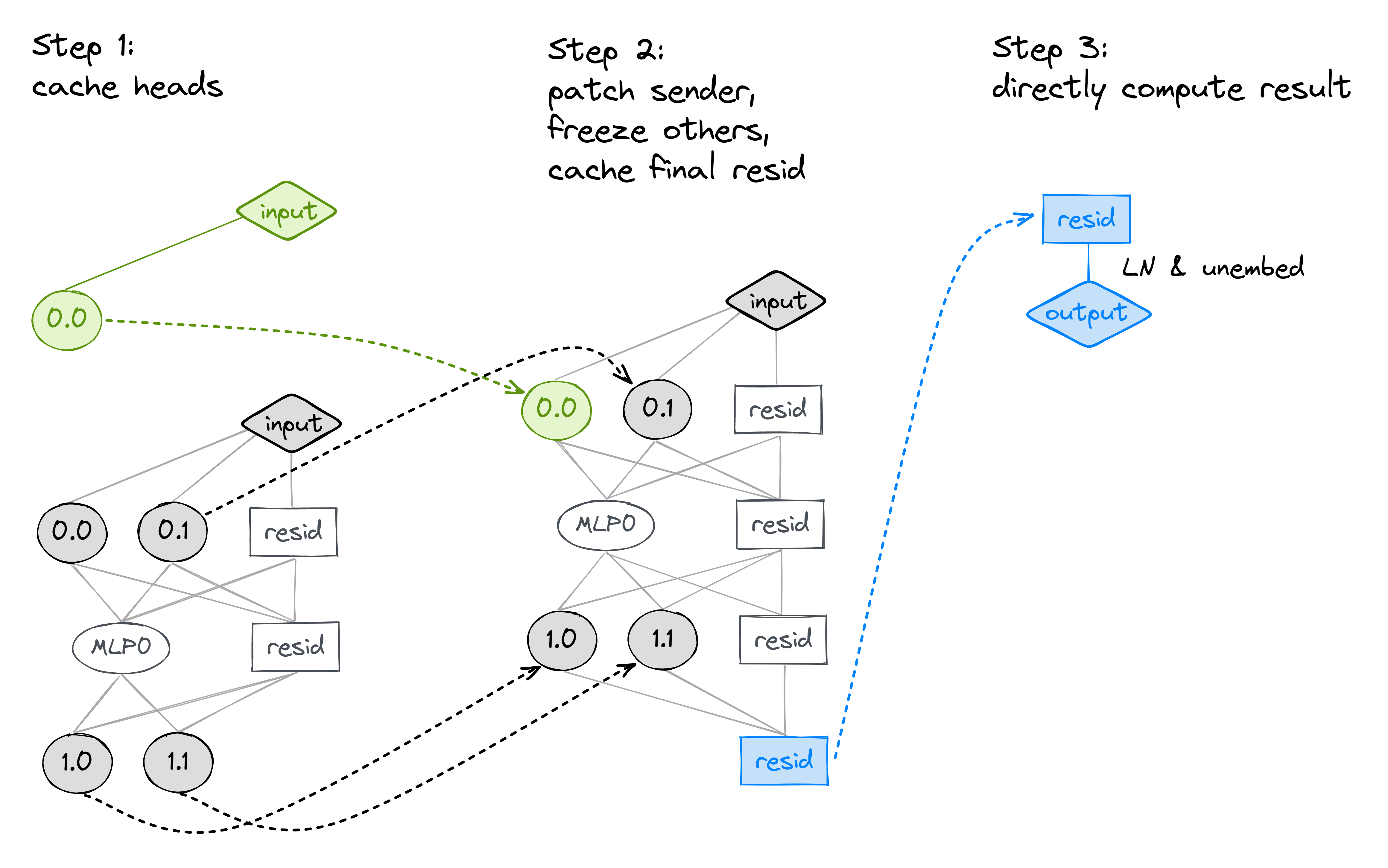
This patching is described at the start of section 3.1 in the paper (page 5). The 3-step process will look like:

1. Run the model on clean and corrupted input. Cache the head outputs.
2. Run the model on clean input, with the sender head patched from the corrupted input, and every other head frozen to their values on the clean input. Cache the final value of the residual stream (i.e. resid_post in the final layer).
3. Normally we would re-run the model on the clean input and patch in the cached value of the final residual stream, but in this case we don't need to because we can just unembed the final value of the residual stream directly without having to run another forward pass.

Here is an illustration for a 2-layer transformer:

Exercise - implement path patching to the final residual stream value

You should implement path patching from heads to the residual stream, as described above (and in the paper).

This exercise is expected to be challenging, with several moving parts. We've purposefully left it very open-ended, including a function & docstring but nothing else.

Here are a few hints / tips for how to proceed:

• Split your function up into 3 parts (one for each of the steps above), and write each section one at a time.
• You'll need a new hook function: one which performs freezing / patching for step 2 of the algorithm.
• You can reuse a lot of code from your activation patching function.
• When calling model.run_with_cache, you can use the keyword argument names_filter, which is a function from name to boolean. If you use this argument, your model will only cache activations with a name which passes this filter (e.g. you can use it like names_filter = lambda name: name.endswith("q") to only cache query vectors).

You can also look at the dropdowns to get more hints and guidance (e.g. if you want to start from a function docstring).

You'll know you've succeeded if you can plot the results, and replicate Figure 3(b) from the paper (at the top of page 6).

Note - if you use model.add_hook then model.run_with_cache, you might have to pass the argument level=1 to the add_hook method. I don't know why the function sometimes fails unless you do this (this bug only started appearing after the exercises were written). I've not had time to track this down, but extra credit to anyone who can (-:

def get_path_patch_head_to_final_resid_post(
    model: HookedTransformer,
    patching_metric: Callable,
    new_dataset: IOIDataset = abc_dataset,
    orig_dataset: IOIDataset = ioi_dataset,
    new_cache: ActivationCache | None = abc_cache,
    orig_cache: ActivationCache | None = ioi_cache,
) -> Float[Tensor, "layer head"]:
    '''
    Performs path patching (see algorithm in appendix B of IOI paper), with:
        sender head = (each head, looped through, one at a time)
        receiver node = final value of residual stream
    Returns:
        tensor of metric values for every possible sender head
    '''
    pass

def get_path_patch_head_to_final_resid_post(
    model: HookedTransformer,
    patching_metric: Callable,
    new_dataset: IOIDataset = abc_dataset,
    orig_dataset: IOIDataset = ioi_dataset,
    new_cache: ActivationCache | None = abc_cache,
    orig_cache: ActivationCache | None = ioi_cache,
) -> Float[Tensor, "layer head"]:
    '''
    Performs path patching (see algorithm in appendix B of IOI paper), with:
        sender head = (each head, looped through, one at a time)
        receiver node = final value of residual stream
    Returns:
        tensor of metric values for every possible sender head
    '''
    model.reset_hooks()
    results = t.zeros(model.cfg.n_layers, model.cfg.n_heads, device=device, dtype=t.float32)
# ========== Step 1 ==========
    # Gather activations on x_orig and x_new
# YOUR CODE HERE
# Using itertools to loop gives us a smoother progress bar (using nested for loops is also fine)
    for (sender_layer, sender_head) in tqdm_notebook(list(itertools.product(
        range(model.cfg.n_layers),
        range(model.cfg.n_heads)
    ))):
        pass
# ========== Step 2 ==========
        # Run on x_orig, with sender head patched from x_new, every other head frozen
# YOUR CODE HERE
# ========== Step 3 ==========
        # Unembed the final residual stream value, to get our patched logits
# YOUR CODE HERE
# Save the results
        results[sender_layer, sender_head] = patching_metric(patched_logits)
return results

def patch_or_freeze_head_vectors(
    orig_head_vector: Float[Tensor, "batch pos head_index d_head"],
    hook: HookPoint,
    new_cache: ActivationCache,
    orig_cache: ActivationCache,
    head_to_patch: tuple[int, int],
) -> Float[Tensor, "batch pos head_index d_head"]:
    """
    This helps implement step 2 of path patching. We freeze all head outputs (i.e. set them to their
    values in orig_cache), except for head_to_patch (if it's in this layer) which we patch with the
    value from new_cache.

    head_to_patch: tuple of (layer, head)
    """
    # Setting using ..., otherwise changing orig_head_vector will edit cache value too
    orig_head_vector[...] = orig_cache[hook.name][...]
    if head_to_patch[0] == hook.layer():
        orig_head_vector[:, :, head_to_patch[1]] = new_cache[hook.name][:, :, head_to_patch[1]]
    return orig_head_vector


def get_path_patch_head_to_final_resid_post(
    model: HookedTransformer,
    patching_metric: Callable,
    new_dataset: IOIDataset = abc_dataset,
    orig_dataset: IOIDataset = ioi_dataset,
    new_cache: ActivationCache | None = abc_cache,
    orig_cache: ActivationCache | None = ioi_cache,
) -> Float[Tensor, "layer head"]:
    """
    Performs path patching (see algorithm in appendix B of IOI paper), with:

        sender head = (each head, looped through, one at a time)
        receiver node = final value of residual stream

    Returns:
        tensor of metric values for every possible sender head
    """
    raise NotImplementedError()


path_patch_head_to_final_resid_post = get_path_patch_head_to_final_resid_post(model, ioi_metric_2)

imshow(
    100 * path_patch_head_to_final_resid_post,
    title="Direct effect on logit difference",
    labels={"x": "Head", "y": "Layer", "color": "Logit diff. variation"},
    coloraxis=dict(colorbar_ticksuffix="%"),
    width=600,
)

x = t.zeros(3)
y = x
x[0] = 1
print(y)

x = t.zeros(3)
y = t.zeros(3)
x[...] = y
x[0] = 1
print(y)

def patch_or_freeze_head_vectors(
    orig_head_vector: Float[Tensor, "batch pos head_index d_head"],
    hook: HookPoint,
    new_cache: ActivationCache,
    orig_cache: ActivationCache,
    head_to_patch: tuple[int, int],
) -> Float[Tensor, "batch pos head_index d_head"]:
    """
    This helps implement step 2 of path patching. We freeze all head outputs (i.e. set them to their
    values in orig_cache), except for head_to_patch (if it's in this layer) which we patch with the
    value from new_cache.
    head_to_patch: tuple of (layer, head)
    """
    # Setting using ..., otherwise changing orig_head_vector will edit cache value too
    orig_head_vector[...] = orig_cache[hook.name][...]
    if head_to_patch[0] == hook.layer():
        orig_head_vector[:, :, head_to_patch[1]] = new_cache[hook.name][:, :, head_to_patch[1]]
    return orig_head_vector
def get_path_patch_head_to_final_resid_post(
    model: HookedTransformer,
    patching_metric: Callable,
    new_dataset: IOIDataset = abc_dataset,
    orig_dataset: IOIDataset = ioi_dataset,
    new_cache: ActivationCache | None = abc_cache,
    orig_cache: ActivationCache | None = ioi_cache,
) -> Float[Tensor, "layer head"]:
    """
    Performs path patching (see algorithm in appendix B of IOI paper), with:
        sender head = (each head, looped through, one at a time)
        receiver node = final value of residual stream
    Returns:
        tensor of metric values for every possible sender head
    """
    model.reset_hooks()
    results = t.zeros(model.cfg.n_layers, model.cfg.n_heads, device=device, dtype=t.float32)
resid_post_hook_name = utils.get_act_name("resid_post", model.cfg.n_layers - 1)
    resid_post_name_filter = lambda name: name == resid_post_hook_name
# ========== Step 1 ==========
    # Gather activations on x_orig and x_new
# Note the use of names_filter for the run_with_cache function. Using it means we
    # only cache the things we need (in this case, just attn head outputs).
    z_name_filter = lambda name: name.endswith("z")
    if new_cache is None:
        _, new_cache = model.run_with_cache(
            new_dataset.toks, names_filter=z_name_filter, return_type=None
        )
    if orig_cache is None:
        _, orig_cache = model.run_with_cache(
            orig_dataset.toks, names_filter=z_name_filter, return_type=None
        )
# Looping over every possible sender head (the receiver is always the final resid_post)
    for sender_layer, sender_head in tqdm(
        list(product(range(model.cfg.n_layers), range(model.cfg.n_heads)))
    ):
        # ========== Step 2 ==========
        # Run on x_orig, with sender head patched from x_new, every other head frozen
hook_fn = partial(
            patch_or_freeze_head_vectors,
            new_cache=new_cache,
            orig_cache=orig_cache,
            head_to_patch=(sender_layer, sender_head),
        )
        model.add_hook(z_name_filter, hook_fn)
_, patched_cache = model.run_with_cache(
            orig_dataset.toks, names_filter=resid_post_name_filter, return_type=None
        )
        # if (sender_layer, sender_head) == (9, 9):
        #     return patched_cache
        assert set(patched_cache.keys()) == {resid_post_hook_name}
# ========== Step 3 ==========
        # Unembed the final residual stream value, to get our patched logits
patched_logits = model.unembed(model.ln_final(patched_cache[resid_post_hook_name]))
# Save the results
        results[sender_layer, sender_head] = patching_metric(patched_logits)
return results
path_patch_head_to_final_resid_post = get_path_patch_head_to_final_resid_post(model, ioi_metric_2)

What is the interpretation of this plot? How does it compare to the equivalent plot we got from activation patching? (Remember that our metric is defined in a different way, so we should expect a sign difference between the two results.)

Path Patching: S-Inhibition Heads

In the first section on path patching, we performed a simple kind of patching - from the output of an attention head to the final value of the residual stream. Here we'll do something a bit more interesting, and patch from the output of one head to the input of a later head. The purpose of this is to examine exactly how two heads are composing, and what effect the composed heads have on the model's output.

We got a hint of this in the previous section, where we patched the values of the S-inhibition heads and found that they were important. But this didn't tell us which inputs to these value vectors were important; we had to make educated guesses about this based on our analysis earlier parts of the model. In path patching, we can perform a more precise test to find which heads are important.

The paper's results from path patching are shown in figure 5(b), on page 7.

Exercise - implement path patching from head to head

You should fill in the function get_path_patch_head_to_head below. It takes as arguments a list of receiver nodes (as well as the type of input - keys, queries, or values), and returns a tensor of shape* (layer, head) where each element is the result of running the patching metric on the output of the model, after applying the 3-step path patching algorithm from one of the model's heads to all the receiver heads. You should be able to replicate the paper's results (figure 5(b)).

*Actually, you don't need to return all layers, because the causal effect from any sender head which is on the same or a later layer than the last of your receiver heads will necessarily be zero.

If you want a bit more guidance, you can use the dropdown below to see the ways in which this function should be different from your first path patching function (in most ways these functions will be similar, so you can start by copying that function).

def patch_head_input(
    orig_activation: Float[Tensor, "batch pos head_idx d_head"],
    hook: HookPoint,
    patched_cache: ActivationCache,
    head_list: list[tuple[int, int]],
) -> Float[Tensor, "batch pos head_idx d_head"]:
    """
    Function which can patch any combination of heads in layers,
    according to the heads in head_list.
    """
    heads_to_patch = [head for layer, head in head_list if layer == hook.layer()]
    orig_activation[:, :, heads_to_patch] = patched_cache[hook.name][:, :, heads_to_patch]
    return orig_activation


def get_path_patch_head_to_heads(
    receiver_heads: list[tuple[int, int]],
    receiver_input: str,
    model: HookedTransformer,
    patching_metric: Callable,
    new_dataset: IOIDataset = abc_dataset,
    orig_dataset: IOIDataset = ioi_dataset,
    new_cache: ActivationCache | None = None,
    orig_cache: ActivationCache | None = None,
) -> Float[Tensor, "layer head"]:
    """
    Performs path patching (see algorithm in appendix B of IOI paper), with:

        sender head = (each head, looped through, one at a time)
        receiver node = input to a later head (or set of heads)

    The receiver node is specified by receiver_heads and receiver_input, for example if
    receiver_input = "v" and receiver_heads = [(8, 6), (8, 10), (7, 9), (7, 3)], we're doing path
    patching from each head to the value inputs of the S-inhibition heads.

    Returns:
        tensor of metric values for every possible sender head
    """
    model.reset_hooks()

    raise NotImplementedError()


model.reset_hooks()

s_inhibition_value_path_patching_results = get_path_patch_head_to_heads(
    receiver_heads=[(8, 6), (8, 10), (7, 9), (7, 3)],
    receiver_input="v",
    model=model,
    patching_metric=ioi_metric_2,
)

imshow(
    100 * s_inhibition_value_path_patching_results,
    title="Direct effect on S-Inhibition Heads' values",
    labels={"x": "Head", "y": "Layer", "color": "Logit diff.<br>variation"},
    width=600,
    coloraxis=dict(colorbar_ticksuffix="%"),
)

def patch_head_input(
    orig_activation: Float[Tensor, "batch pos head_idx d_head"],
    hook: HookPoint,
    patched_cache: ActivationCache,
    head_list: list[tuple[int, int]],
) -> Float[Tensor, "batch pos head_idx d_head"]:
    """
    Function which can patch any combination of heads in layers,
    according to the heads in head_list.
    """
    heads_to_patch = [head for layer, head in head_list if layer == hook.layer()]
    orig_activation[:, :, heads_to_patch] = patched_cache[hook.name][:, :, heads_to_patch]
    return orig_activation
def get_path_patch_head_to_heads(
    receiver_heads: list[tuple[int, int]],
    receiver_input: str,
    model: HookedTransformer,
    patching_metric: Callable,
    new_dataset: IOIDataset = abc_dataset,
    orig_dataset: IOIDataset = ioi_dataset,
    new_cache: ActivationCache | None = None,
    orig_cache: ActivationCache | None = None,
) -> Float[Tensor, "layer head"]:
    """
    Performs path patching (see algorithm in appendix B of IOI paper), with:
        sender head = (each head, looped through, one at a time)
        receiver node = input to a later head (or set of heads)
    The receiver node is specified by receiver_heads and receiver_input, for example if
    receiver_input = "v" and receiver_heads = [(8, 6), (8, 10), (7, 9), (7, 3)], we're doing path
    patching from each head to the value inputs of the S-inhibition heads.
    Returns:
        tensor of metric values for every possible sender head
    """
    model.reset_hooks()
assert receiver_input in ("k", "q", "v")
    receiver_layers = set(next(zip(*receiver_heads)))
    receiver_hook_names = [utils.get_act_name(receiver_input, layer) for layer in receiver_layers]
    receiver_hook_names_filter = lambda name: name in receiver_hook_names
results = t.zeros(max(receiver_layers), model.cfg.n_heads, device=device, dtype=t.float32)
# ========== Step 1 ==========
    # Gather activations on x_orig and x_new
# Note the use of names_filter for the run_with_cache function. Using it means we
    # only cache the things we need (in this case, just attn head outputs).
    z_name_filter = lambda name: name.endswith("z")
    if new_cache is None:
        _, new_cache = model.run_with_cache(
            new_dataset.toks, names_filter=z_name_filter, return_type=None
        )
    if orig_cache is None:
        _, orig_cache = model.run_with_cache(
            orig_dataset.toks, names_filter=z_name_filter, return_type=None
        )
# Note, the sender layer will always be before the final receiver layer, otherwise there will
    # be no causal effect from sender -> receiver. So we only need to loop this far.
    for sender_layer, sender_head in tqdm(
        list(product(range(max(receiver_layers)), range(model.cfg.n_heads)))
    ):
        # ========== Step 2 ==========
        # Run on x_orig, with sender head patched from x_new, every other head frozen
hook_fn = partial(
            patch_or_freeze_head_vectors,
            new_cache=new_cache,
            orig_cache=orig_cache,
            head_to_patch=(sender_layer, sender_head),
        )
        model.add_hook(z_name_filter, hook_fn, level=1)
_, patched_cache = model.run_with_cache(
            orig_dataset.toks, names_filter=receiver_hook_names_filter, return_type=None
        )
        # model.reset_hooks(including_permanent=True)
        assert set(patched_cache.keys()) == set(receiver_hook_names)
# ========== Step 3 ==========
        # Run on x_orig, patching in the receiver node(s) from the previously cached value
hook_fn = partial(
            patch_head_input,
            patched_cache=patched_cache,
            head_list=receiver_heads,
        )
        patched_logits = model.run_with_hooks(
            orig_dataset.toks,
            fwd_hooks=[(receiver_hook_names_filter, hook_fn)],
            return_type="logits",
        )
# Save the results
        results[sender_layer, sender_head] = patching_metric(patched_logits)
return results
model.reset_hooks()
s_inhibition_value_path_patching_results = get_path_patch_head_to_heads(
    receiver_heads=[(8, 6), (8, 10), (7, 9), (7, 3)],
    receiver_input="v",
    model=model,
    patching_metric=ioi_metric_2,
)