4️⃣ Sampling from a Transformer
Learning Objectives
- Learn how to sample from a transformer
- This includes basic methods like greedy search or top-k, and more advanced methods like beam search
- Learn how to cache the output of a transformer, so that it can be used to generate text more efficiently
- Optionally, rewrite your sampling functions to make use of your caching methods
Let's discuss how we might go about producing output from a transformer.
One obvious method to sample tokens from a distribution would be to always take the token assigned the highest probability. But this can lead to some boring and repetitive outcomes, and at worst it can lock our transformer's output into a loop.
First, you should read HuggingFace's blog post How to generate text: using different decoding methods for language generation with Transformers. Once you've done that, you can start the exercises below.
TransformerSampler class
Below, we've given you the TransformerSampler class. This contains the following important methods:
sample, which is the highest-level method. It repeatedly callssample_next_tokento generate new tokens, until one of the termination criteria is met.sample_next_token, which samples a single new token based on some hyperparameters. This might involve various different sampling methods and techniques e.g. temperature scaling, top-k sampling, top-p sampling, etc.- A set of other methods, which apply the previously mentioned sampling methods and techniques.
You can see how sample_next_token works, and as an example how greedy sampling is implemented via greedy_search - we just continually take the tokens with the highest logits at each step.
Question - why do you think temperature=0.0 correspond to greedy sampling?
To apply a temperature to our sampling (as we'll see later) means to scale all logits by (1 / temperature). The basic intuition here is:
As temperature gets close to zero, the difference between the largest logit and second largest logit becomes very large, so the distribution tends to "probability of 1 on the highest-likelihood token", i.e. greedy sampling. You can derive this formally if you prefer.
In the next exercise you'll implement the sample method, and then you'll go on to implement all the other methods.
Exercise - implement sample
The sample method generates new tokens autoregressively, by repeatedly:
- Passing the current sequence of tokens through the model to get logits,
- Using some sampling technique to select a new token, i.e.
sample_next_token(input_ids, logits, **kwargs), - Appending this new token to the input sequence,
- Repeating the process until one of the termination criteria is met: either we generate
max_tokens_generatednew tokens, or we generate the end-of-sequence token (which we can access viaself.tokenizer.eos_token_id).
Lastly, we use the tokenizer.decode method to return the sampled string. You're also invited to use the verbose argument, for printing the decoded sequences while they're being generated (this can help with debugging).
Below is some code which tests your sampling function by performing greedy sampling (which means always choosing the most likely next token at each step).
A few hints:
- Don't forget about tensor shapes! Your model's input should always have a batch dimension, i.e. it should be shape
(1, seq_len). - The
sample_next_tokenmethod will return an integer, so make sure you wrap this in a tensor before concatenating it to the end of your input IDs. - Also remember to have your tensors be on the same device (we have a global
devicevariable). - Remember to put your model in evaluation mode, using
model.eval().
class TransformerSampler:
def __init__(self, model: DemoTransformer, tokenizer: GPT2TokenizerFast):
self.model = model
self.cfg = model.cfg
self.tokenizer = tokenizer
@t.inference_mode()
def sample(self, prompt: str, max_tokens_generated=100, verbose=False, **kwargs) -> str:
"""
Returns a string of autoregressively generated text, starting from the prompt.
Sampling terminates at max_tokens_generated, or when the model generates an end-of-sequence token. kwargs are
passed to sample_next_token, to give detailed instructions on how new tokens are chosen.
"""
raise NotImplementedError()
@staticmethod
def sample_next_token(
input_ids: Int[Tensor, "seq_len"],
logits: Float[Tensor, "d_vocab"],
temperature=1.0,
top_k=0,
top_p=0.0,
frequency_penalty=0.0,
seed=None,
) -> int:
assert input_ids.ndim == 1, "input_ids should be a 1D sequence of token ids"
assert temperature >= 0, "Temperature should be non-negative"
assert 0 <= top_p <= 1.0, "Top-p must be a probability"
assert 0 <= top_k, "Top-k must be non-negative"
assert not (top_p != 0 and top_k != 0), "At most one of top-p and top-k supported"
# Set random seeds for reproducibility
if seed is not None:
t.manual_seed(seed)
np.random.seed(seed)
# Apply all the specialized sampling methods
if temperature == 0:
return TransformerSampler.greedy_search(logits)
elif temperature != 1.0:
logits = TransformerSampler.apply_temperature(logits, temperature)
if frequency_penalty != 0.0:
logits = TransformerSampler.apply_frequency_penalty(
input_ids, logits, frequency_penalty
)
if top_k > 0:
return TransformerSampler.sample_top_k(logits, top_k)
if top_p > 0.0:
return TransformerSampler.sample_top_p(logits, top_p)
return TransformerSampler.sample_basic(logits)
@staticmethod
def greedy_search(logits: Float[Tensor, "d_vocab"]) -> int:
"""
Returns the most likely token (as an int).
"""
raise NotImplementedError()
@staticmethod
def apply_temperature(
logits: Float[Tensor, "d_vocab"], temperature: float
) -> Float[Tensor, "d_vocab"]:
"""
Applies temperature scaling to the logits.
"""
raise NotImplementedError()
@staticmethod
def apply_frequency_penalty(
input_ids: Int[Tensor, "seq_len"], logits: Float[Tensor, "d_vocab"], freq_penalty: float
) -> Float[Tensor, "d_vocab"]:
"""
Applies a frequency penalty to the logits.
"""
raise NotImplementedError()
@staticmethod
def sample_basic(logits: Float[Tensor, "d_vocab"]) -> int:
"""
Samples from the distribution defined by the logits.
"""
raise NotImplementedError()
@staticmethod
def sample_top_k(logits: Float[Tensor, "d_vocab"], k: int) -> int:
"""
Samples from the top k most likely tokens.
"""
raise NotImplementedError()
@staticmethod
def sample_top_p(
logits: Float[Tensor, "d_vocab"], top_p: float, min_tokens_to_keep: int = 1
) -> int:
"""
Samples from the most likely tokens which make up at least p cumulative probability.
"""
raise NotImplementedError()
@t.inference_mode()
def beam_search(
self,
prompt: str,
num_return_sequences: int,
num_beams: int,
max_new_tokens: int,
no_repeat_ngram_size: int | None = None,
) -> list[tuple[float, str]]:
"""
Implements a beam search, by repeatedly performing the `generate` and `filter` steps (starting from the initial
prompt) until either of the two stopping criteria are met: (1) we've generated `max_new_tokens` tokens, or (2)
we've generated `num_returns_sequences` terminating sequences.
"""
raise NotImplementedError()
t.set_grad_enabled(False) # gradients are not necessary for sampling
model = DemoTransformer(Config()).to(device)
model.load_state_dict(reference_gpt2.state_dict(), strict=False)
tokenizer = reference_gpt2.tokenizer
sampler = TransformerSampler(model, tokenizer)
prompt = "Jingle bells, jingle bells, jingle all the way"
print(f"Testing greedy decoding\nPrompt: {prompt!r}")
expected = "Jingle bells, jingle bells, jingle all the way up to the top of the mountain."
output = sampler.sample(prompt, max_tokens_generated=8, temperature=0.0)
print(f"Expected: {expected!r}\nActual: {output!r}\n")
assert output == expected
print("Tests passed!")
Solution
@t.inference_mode()
def sample(self, prompt: str, max_tokens_generated=100, verbose=False, kwargs):
"""
Returns a string of autoregressively generated text, starting from the prompt.
Sampling terminates at max_tokens_generated, or when the model generates an end-of-sequence token. kwargs are
passed to sample_next_token, to give detailed instructions on how new tokens are chosen.
"""
self.model.eval()
input_ids = self.tokenizer.encode(prompt, return_tensors="pt").to(device)[0]
for i in range(max_tokens_generated):
# Get new logits (make sure we don't pass in more tokens than the model's context length)
logits = self.model(input_ids[None, -self.cfg.n_ctx :])
# We only take logits for the last token, because this is what we're sampling
logits = logits[0, -1]
# Get next token (as a tensor of size (1, 1) so we can concat it to input_ids)
next_token = t.tensor([TransformerSampler.sample_next_token(input_ids, logits, kwargs)], device=device)
# Create new input ids string, with shape (1, old_seq_len + 1)
input_ids = t.cat([input_ids, next_token], dim=-1)
# Print out results, if required
if verbose:
print(self.tokenizer.decode(input_ids), end="\r")
# If our new token was the end-of-text token, stop
if next_token == getattr(self.tokenizer, "eos_token_id", None):
break
return self.tokenizer.decode(input_ids)
Sampling with Categorical
Now, we'll move into implementing specific sampling methods. In each of these cases, you should return to the class definition above and fill in the corresponding method.
PyTorch provides a distributions package with a number of convenient methods for sampling from various distributions.
For now, we just need t.distributions.categorical.Categorical. Use this to implement sample_basic, which just samples from the provided logits (which may have already been modified by the temperature and frequency penalties).
Note that this will be slow since we aren't batching the samples, but don't worry about speed for now.
Exercise - sample_basic
Implement basic sampling in the TransformerSampler class above (i.e. the sample_basic method), then run the code below to verify your solution works.
prompt = "John and Mary went to the"
input_ids = tokenizer.encode(prompt, return_tensors="pt").to(device)
logits = model(input_ids)[0, -1]
expected_top_5 = {
" church": 0.0648,
" house": 0.0367,
" temple": 0.0145,
" same": 0.0104,
" Church": 0.0097,
}
frequency_of_top_5 = defaultdict(int)
N = 10_000
for _ in tqdm(range(N)):
token = TransformerSampler.sample_next_token(input_ids.squeeze(), logits)
frequency_of_top_5[tokenizer.decode(token)] += 1
for word in expected_top_5:
expected_freq = expected_top_5[word]
observed_freq = frequency_of_top_5[word] / N
print(
f"Word: {word!r:<9}. Expected freq {expected_freq:.4f}, observed freq {observed_freq:.4f}"
)
assert abs(observed_freq - expected_freq) < 0.01, (
"Try increasing N if this fails by a small amount."
)
print("Tests passed!")
Solution
@staticmethod
def sample_basic(logits: Float[Tensor, "d_vocab"]) -> int:
"""
Samples from the distribution defined by the logits.
"""
sampled_token = t.distributions.categorical.Categorical(logits=logits).sample()
return sampled_token.item()
Exercise - apply_temperature
Temperature sounds fancy, but it's literally just dividing the logits by the temperature. You should implement this in your TransformerSampler class now.
logits = t.tensor([1, 2]).log()
cold_logits = TransformerSampler.apply_temperature(logits, temperature=0.001)
print('A low temperature "sharpens" or "peaks" the distribution: ', cold_logits)
t.testing.assert_close(cold_logits, 1000.0 * logits)
hot_logits = TransformerSampler.apply_temperature(logits, temperature=1000.0)
print("A high temperature flattens the distribution: ", hot_logits)
t.testing.assert_close(hot_logits, 0.001 * logits)
print("Tests passed!")
Solution
@staticmethod
def apply_temperature(logits: Float[Tensor, "d_vocab"], temperature: float) -> Float[Tensor, "d_vocab"]:
"""
Applies temperature scaling to the logits.
"""
return logits / temperature
Exercise - apply_frequency_penalty
The frequency penalty is simple as well: count the number of occurrences of each token, then subtract freq_penalty for each occurrence. Hint: use t.bincount (documentation here) to do this in a vectorized way.
You should implement the apply_frequency_penalty method in your TransformerSampler class now, then run the cell below to check your solution.
Help - I'm getting a RuntimeError; my tensor sizes don't match.
Look at the documentation page for t.bincount. You might need to use the minlength argument - why?
bieber_prompt = "And I was like Baby, baby, baby, oh Like, Baby, baby, baby, no Like, Baby, baby, baby, oh I thought you'd always be mine, mine"
input_ids = tokenizer.encode(bieber_prompt, return_tensors="pt")
logits = t.ones(tokenizer.vocab_size)
penalized_logits = TransformerSampler.apply_frequency_penalty(input_ids.squeeze(), logits, 2.0)
assert penalized_logits[5156].item() == -11, (
"Expected 6 occurrences of ' baby' with leading space, 1-2*6=-11"
)
assert penalized_logits[14801].item() == -5, (
"Expected 3 occurrences of ' Baby' with leading space, 1-2*3=-5"
)
print("Tests passed!")
Solution
@staticmethod
def apply_frequency_penalty(
input_ids: Int[Tensor, "seq_len"], logits: Float[Tensor, "d_vocab"], freq_penalty: float
) -> Float[Tensor, "d_vocab"]:
"""
Applies a frequency penalty to the logits.
"""
d_vocab = logits.size(0)
id_freqs = t.bincount(input_ids, minlength=d_vocab)
return logits - freq_penalty * id_freqs
Sampling - Manual Testing
Run the below cell to get a sense for the temperature and freq_penalty arguments. Play with your own prompt and try other values.
Note: your model can generate newlines or non-printing characters, so calling print on generated text sometimes looks awkward on screen. You can call repr on the string before printing to have the string escaped nicely.
sampler = TransformerSampler(model, tokenizer)
N_RUNS = 1
your_prompt = "Jingle bells, jingle bells, jingle all the way"
cases = [
("High freq penalty", dict(frequency_penalty=100.0)),
("Negative freq penalty", dict(frequency_penalty=-3.0)),
("Too hot!", dict(temperature=2.0)),
("Pleasantly cool", dict(temperature=0.7)),
("Pleasantly warm", dict(temperature=0.9)),
("Too cold!", dict(temperature=0.01)),
]
table = Table("Name", "Kwargs", "Output", title="Sampling - Manual Testing")
for name, kwargs in cases:
for i in range(N_RUNS):
output = sampler.sample(your_prompt, max_tokens_generated=24, **kwargs)
table.add_row(name, str(kwargs), repr(output) + "\n")
rprint(table)
Click to see the expected output
Sampling - Manual Testing ┏━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Name ┃ Kwargs ┃ Output ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ High freq penalty │ {'frequency_penalty': 100.0} │ 'Jingle bells, jingle bells, jingle all the way │ │ │ │ down.\nBe Parlearan - Be pararellane... I wanna touch it │ │ │ │ where? + Cut and meet' │ │ │ │ │ │ Negative freq penalty │ {'frequency_penalty': -3.0} │ 'Jingle bells, jingle bells, jingle all the way, jingle, │ │ │ │ jingle, jingle, jingle, jingle, jingle, jingle, jingle' │ │ │ │ │ │ Too hot! │ {'temperature': 2.0} │ 'Jingle bells, jingle bells, jingle all the way wild │ │ │ │ Britain freemen/(aden forks dumping inhibits steel III │ │ │ │ Decathlonsuitgirls override drunk lockdown mirror issues │ │ │ │ under totally monopolish' │ │ │ │ │ │ Pleasantly cool │ {'temperature': 0.7} │ 'Jingle bells, jingle bells, jingle all the way around. │ │ │ │ But, I am not even in the mood to hear you. You are my │ │ │ │ friend. And the only one' │ │ │ │ │ │ Pleasantly warm │ {'temperature': 0.9} │ "Jingle bells, jingle bells, jingle all the way up and │ │ │ │ down it's a song.\n\nThe third thing that's interesting │ │ │ │ is coach Pugh, he actually likes" │ │ │ │ │ │ Too cold! │ {'temperature': 0.01} │ 'Jingle bells, jingle bells, jingle all the way up to │ │ │ │ the top of the mountain.\n\nThe first time I saw the │ │ │ │ mountain, I was in the middle of' │ │ │ │ │ └───────────────────────┴──────────────────────────────┴──────────────────────────────────────────────────────────┘
Top-K Sampling
Conceptually, the steps in top-k sampling are:
- Find the top_k largest probabilities (you can use torch.topk)
- Set all other probabilities to zero
- Normalize and sample
Exercise - sample_top_k
Implement the method sample_top_k now. Your implementation should stay in log-space throughout (don't exponentiate to obtain probabilities). This means you don't actually need to worry about normalizing, because Categorical accepts unnormalised logits.
prompt = "John and Mary went to the"
input_ids = tokenizer.encode(prompt, return_tensors="pt").to(device)
logits = model(input_ids)[0, -1]
expected_top_5 = {
" church": 0.0648,
" house": 0.0367,
" temple": 0.0145,
" same": 0.0104,
" Church": 0.0097,
}
topk_5_sum = sum(expected_top_5.values())
observed_freqs = defaultdict(int)
N = 10000
for _ in tqdm(range(N)):
token = TransformerSampler.sample_next_token(input_ids.squeeze(), logits, top_k=5)
observed_freqs[tokenizer.decode(token)] += 1
for word in expected_top_5:
expected_freq = expected_top_5[word] / topk_5_sum
observed_freq = observed_freqs[word] / N
print(
f"Word: {word!r:<9}. Expected freq = {expected_freq:.4f}, observed freq = {observed_freq:.4f}"
)
assert abs(observed_freq - expected_freq) < 0.01
Solution
@staticmethod
def sample_top_k(logits: Float[Tensor, "d_vocab"], k: int) -> int:
"""
Samples from the top k most likely tokens.
"""
top_k_logits, top_k_token_ids = logits.topk(k)
# Get sampled token (which is an index corresponding to the list of top-k tokens)
sampled_token_idx = t.distributions.categorical.Categorical(logits=top_k_logits).sample()
# Get the actual token id, as an int
return top_k_token_ids[sampled_token_idx].item()
The GPT-2 paper famously included an example prompt about unicorns. Now it's your turn to see just how cherry picked this example was.
The paper claims they used top_k=40 and best of 10 samples.
sampler = TransformerSampler(model, tokenizer)
your_prompt = "In a shocking finding, scientist discovered a herd of unicorns living in a remote, previously unexplored valley, in the Andes Mountains. Even more surprising to the researchers was the fact that the unicorns spoke perfect English."
output = sampler.sample(your_prompt, temperature=0.7, top_k=40, max_tokens_generated=64)
rprint(f"Your model said:\n\n[bold dark_orange]{output}")
Click to see the expected output
Your model said: In a shocking finding, scientist discovered a herd of unicorns living in a remote, previously unexplored valley, in the Andes Mountains. Even more surprising to the researchers was the fact that the unicorns spoke perfect English. "This shows that there are two distinct kinds of unicorns that live in the Andes," says lead author Dr. Andrew Wysocki. "The first is called the wild unicorn, which is the most common type." These unicorns, which are called bunnies, are most common
This is pretty incredible! For some perspective on how much of a paradigm shift even basic models like this represented, we recommend reading this section from Simulators.
Top-p aka Nucleus Sampling
The basic idea is that we choose the most likely words, up until the total probability of words we've chosen crosses some threshold. Then we sample from those chosen words based on their logits.
The steps are:
- Sort the probabilities from largest to smallest
- Find the cutoff point where the cumulative probability first equals or exceeds
top_p. We do the cutoff inclusively, keeping the first probability above the threshold. - If the number of kept probabilities is less than
min_tokens_to_keep, keep that many tokens instead. - Set all other probabilities to zero
- Normalize and sample
For example, if our probabilities were (0.4, 0.3, 0.2, 0.1) and our cutoff was top_p=0.8, then we'd sample from the first three elements (because their total probability is 0.9 which is over the threshold, but the first two only have a total prob of 0.7 which is under the threshold). Once we've chosen to sample from those three, we would renormalise them by dividing by their sum, so the probabilities we use when sampling are (0.4/0.9, 0.3/0.9, 0.2/0.9).
Optionally, refer to the paper The Curious Case of Neural Text Degeneration for some comparison of different methods.
Exercise - sample_top_p
prompt = "John and Mary went to the"
input_ids = tokenizer.encode(prompt, return_tensors="pt").to(device)
logits = model(input_ids)[0, -1]
expected_top_10pct = {
" church": 0.0648,
" house": 0.0367, # These are the two most likely tokens, and add up to >10%
}
top_10pct_sum = sum(expected_top_10pct.values())
observed_freqs = defaultdict(int)
N = 10_000
for _ in tqdm(range(N)):
token = TransformerSampler.sample_next_token(input_ids.squeeze(), logits, top_p=0.1)
observed_freqs[tokenizer.decode(token)] += 1
for word in expected_top_10pct:
expected_freq = expected_top_10pct[word] / top_10pct_sum
observed_freq = observed_freqs[word] / N
print(
f"Word: {word!r:<9}. Expected freq {expected_freq:.4f}, observed freq {observed_freq:.4f}"
)
assert abs(observed_freq - expected_freq) < 0.01, (
"Try increasing N if this fails by a small amount."
)
Help - I'm stuck on how to implement this function.
First, sort the logits using the sort(descending=True) method (this returns values and indices). Then you can get cumulative_probs by applying softmax to these logits and taking the cumsum. Then, you can decide how many probabilities to keep by using the t.searchsorted function.
Once you've decided which probabilities to keep, it's easiest to sample from them using the original logits (you should have preserved the indices when you called logits.sort). This way, you don't need to worry about renormalising like you would if you were using probabilities.
Solution
@staticmethod
def sample_top_p(logits: Float[Tensor, "d_vocab"], top_p: float, min_tokens_to_keep: int = 1) -> int:
"""
Samples from the most likely tokens which make up at least p cumulative probability.
"""
# Sort logits, and get cumulative probabilities
logits_sorted, indices = logits.sort(descending=True, stable=True)
cumul_probs = logits_sorted.softmax(-1).cumsum(-1)
# Choose which tokens to keep, in the set we sample from
n_keep = t.searchsorted(cumul_probs, top_p, side="left").item() + 1
n_keep = max(n_keep, min_tokens_to_keep)
keep_idx = indices[:n_keep]
keep_logits = logits[keep_idx]
# Perform the sampling
sample = t.distributions.categorical.Categorical(logits=keep_logits).sample()
return keep_idx[sample].item()
Now, an example of top-p sampling:
sampler = TransformerSampler(model, tokenizer)
your_prompt = "Eliezer Shlomo Yudkowsky (born September 11, 1979) is an American decision and artificial intelligence (AI) theorist and writer, best known for"
output = sampler.sample(your_prompt, temperature=0.7, top_p=0.95, max_tokens_generated=64)
rprint(f"Your model said:\n\n[bold dark_orange]{output}")
Click to see the expected output (you might get different results due to randomness)
Your model said: Eliezer Shlomo Yudkowsky (born September 11, 1979) is an American decision and artificial intelligence (AI) theorist and writer, best known for his seminal paper on the "The Matrix" which is about the "futurist" character of the Matrix. He has written numerous books on the subject and is the author of the forthcoming book "The Matrix: Artificial Intelligence and the Matrix Theory", available from the author's website at: http://www.m
Beam search
Finally, we'll implement a more advanced way of searching over output: beam search. You should read the HuggingFace page on beam search before moving on.
In beam search, we maintain a list of size num_beams completions which are the most likely completions so far as measured by the product of their probabilities. Since this product can become very small, we use the sum of log probabilities instead. Note - log probabilities are not the same as your model's output. We get log probabilities by first taking softmax of our output and then taking log. You can do this with the log_softmax function / tensor method.
Log probabilities are equal to the logit output after being translated by some amount X (where X is a function of the original logit output). Can you prove this?
Suppose our vector of logits is $x$, and we take softmax to get a vector of probabilities $p$, then log again to get a vector of log probabilities $l$. Then the $i$-th element of this vector of logprobs is:
where $C = \log \sum_j \exp(x_j)$ is the same for all elements. So we can see that $l_i$ is equal to the logit output $x_i$ after being translated by $C$.
It's important not to mix up logits and logprobs!
Why do you think we use log softmax rather than logit output?
Logit output is translation invariant. If we had two different beams and we were generating the next tokens in those beams, there would be no reasonable way to compare the two beams to each other, because we could shift the logit vector for one beam by a constant amount without changing the distribution.
At each iteration, we run the batch of completions through the model and take the log-softmax to obtain d_vocab log-probs for each completion, or num_beams * d_vocab possible next completions in total.
If we kept all of these, then we would have num_beams * d_vocab * d_vocab completions after the next iteration which is way too many, so instead we sort them by their score and loop through from best (highest) log probability to worst (lowest).
The illustration below might help (based on real results from this method). Here, we have the following hyperparameters:
num_beams = 3
max_new_tokens = 3
num_return_sequences = 2
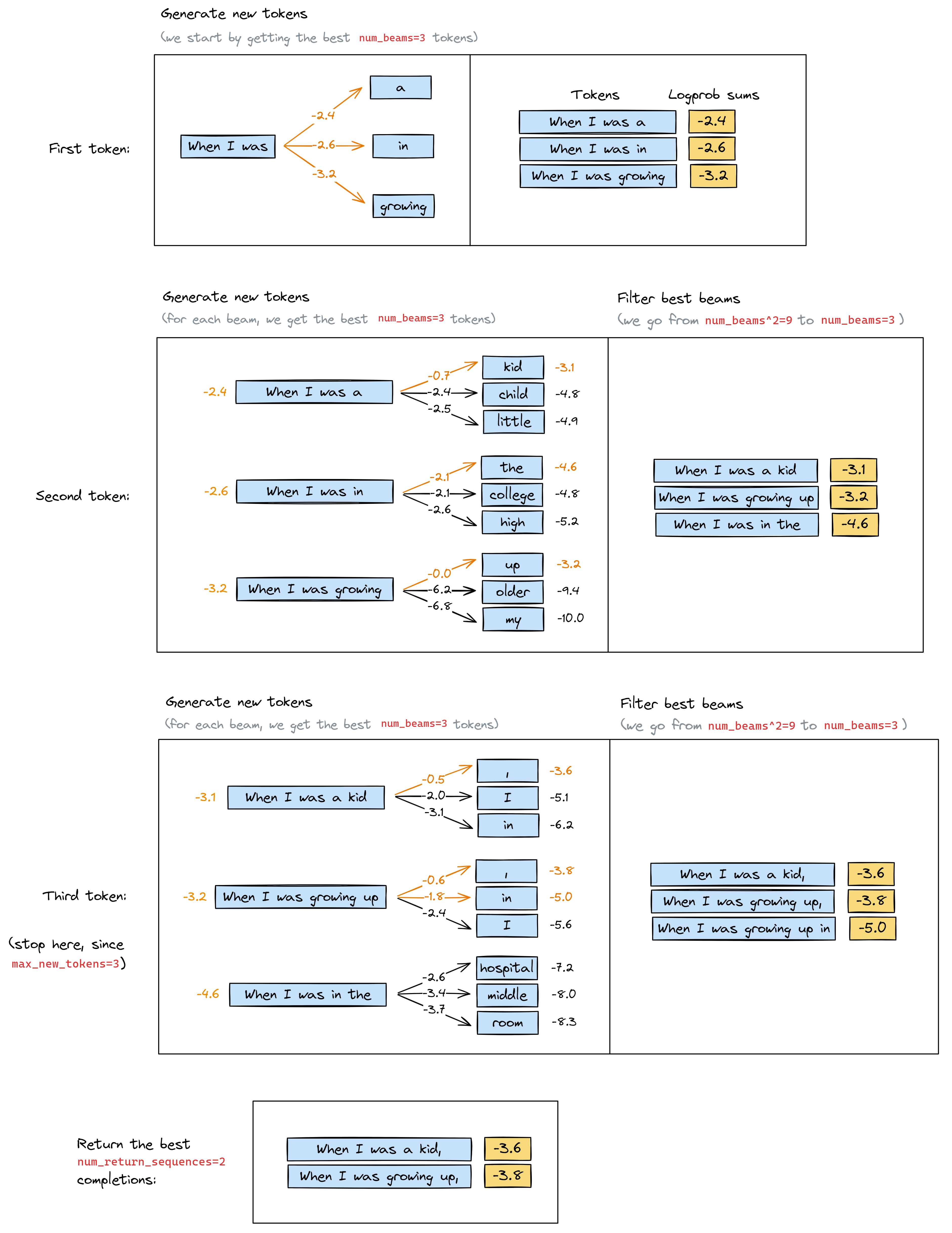
Note how after each "generate" stage, we have num_beams ** 2 possible completions, which we then filter down to num_beams. This is because we need this many in order to find the best num_beams completions overall - for example, it's possible that all the best beams of length n+1 come from the same beam of length n, in which case we'll need to keep all num_beams that we generated from that single beam.
How do we deal with sequences that terminate early (i.e. by generating an EOS token)? Answer - we append them to the list of completions which we'll return at the end, and remove them from the generation tree. Our algorithm terminates when either all our sequences have length max_new_tokens larger than the initial prompt length, or we've generated num_returns_sequences terminating sequences.
Exercise - implement beam_search
We've given you one implementation of beam_search below, which calls the generate and filter methods of the Beams class (these correspond to the two stages in the diagram above). The beam_search method works as follows:
- Create a list
final_logprobs_and_completionsfor storing the final output, as tuples of (logprob sum, string completion). - Perform
max_new_tokenssteps of generation (producing a new set of beams) and filtering (getting the best beams from these combinations), while also adding terminated beams to the list of best beams - Return these terminated beams plus the best ones we have at the end of the steps.
So all you need to do is fill in the generate and filter methods. Below, you'll find some unit tests for the generate and filter methods. When you've passed these tests, you should be able to run the full beam_search function.
Important note - by default, beam search produces a lot of repeated words / phrases / sentences. This makes sense - if the model finds some completion with a much higher logit sum than most completions in its beam search space, then it will want to repeat this completion even if it doesn't make a lot of sense in context. A common solution is to ban repetition of n-grams, which you should also implement in the function below. In other words, rather than sampling tokens from each sequence by taking logprobs.topk(k) in your generate method, you should take the k top tokens after filtering out those that give you repeated n-grams of length no_repeat_ngram_size. Good values of this parameter to try are 2 or 3 (although we recommend you try without this parameter first, so you can see how much of a difference it makes!).
@dataclass
class Beams:
"""Class to store beams during beam search."""
model: DemoTransformer
tokenizer: GPT2TokenizerFast
logprob_sums: Float[Tensor, "batch"]
tokens: Int[Tensor, "batch seq"]
def __getitem__(self, batch_idx) -> "Beams":
"""Allows you to create new beams from old beams by slicing along batch dim (useful for `filter`)."""
return Beams(
self.model, self.tokenizer, self.logprob_sums[batch_idx], self.tokens[batch_idx]
)
@property
def logprobs_and_completions(self) -> list[tuple[float, str]]:
"""Returns self as a list of logprob sums and completions (useful for getting final output)."""
return [
(logprob_sum.item(), self.tokenizer.decode(tokens))
for (logprob_sum, tokens) in zip(self.logprob_sums, self.tokens)
]
def generate(self, k: int, no_repeat_ngram_size: int | None = None) -> "Beams":
"""
Starting from the current set of beams (i.e. self.tokens) and returns a new set of `len(self.tokens) * k` beams,
containing the best `k` continuations for each of the original beams.
Optional argument `no_repeat_ngram_size` means your model won't generate any sequences with a repeating n-gram
of this length.
"""
raise NotImplementedError()
def filter(self, k: int) -> tuple["Beams", "Beams"]:
"""
Returns:
best_beams: Beams
filtered version of self, containing all best `k` which are also not terminated.
early_terminations: Beams
filtered version of self, containing all best `k` which are also terminated.
"""
raise NotImplementedError()
def print(self, title="Best completions", max_print_chars=80) -> None:
"""
Prints out a set of sequences with their corresponding logprob sums.
"""
if len(self.tokens) == 0:
return
table = Table("logprob sum", "completion", title=title)
for logprob_sum, tokens in zip(self.logprob_sums, self.tokens):
text = self.tokenizer.decode(tokens)
if len(repr(text)) > max_print_chars:
text = (
text[: int(0.3 * max_print_chars)]
+ " ... "
+ text[-int(0.7 * max_print_chars) :]
)
table.add_row(f"{logprob_sum:>8.3f}", repr(text))
rprint(table)
@t.inference_mode()
def beam_search(
self: TransformerSampler,
prompt: str,
num_return_sequences: int,
num_beams: int,
max_new_tokens: int,
no_repeat_ngram_size: int | None = None,
) -> list[tuple[float, str]]:
"""
Implements a beam search, by repeatedly performing the `generate` and `filter` steps (starting from the initial
prompt) until either of the two stopping criteria are met: (1) we've generated `max_new_tokens` tokens, or (2)
we've generated `num_returns_sequences` terminating sequences.
"""
assert num_return_sequences <= num_beams
self.model.eval()
tokens = self.tokenizer.encode(prompt, return_tensors="pt").to(device)
final_logprobs_and_completions = [] # we add to this list as we get terminated beams
best_beams = Beams(
self.model, self.tokenizer, t.tensor([0.0]).to(device), tokens
) # start with just 1 beam
for _ in tqdm(range(max_new_tokens)):
t.cuda.empty_cache()
# Generate & filter beams
best_beams = best_beams.generate(k=num_beams, no_repeat_ngram_size=no_repeat_ngram_size)
best_beams, best_beams_terminated = best_beams.filter(k=num_beams)
# Add terminated beams to our list, and return early if we have enough
final_logprobs_and_completions.extend(best_beams_terminated.logprobs_and_completions)
if len(final_logprobs_and_completions) >= num_return_sequences:
return final_logprobs_and_completions[:num_return_sequences]
# Return terminated beams plus the best ongoing beams of length `orig_len + max_new_tokens`
final_logprobs_and_completions.extend(best_beams.logprobs_and_completions)
return final_logprobs_and_completions[:num_return_sequences]
TransformerSampler.beam_search = beam_search
Help - I'm stuck on the implementation of no_repeat_ngram_size.
Here's a method, which you can use in your generate function in place of logprobs.topk(k), which filters out the ngrams of length no_repeat_ngram_size which have already appeared in self.tokens:
def get_topk_non_repeating(
self,
logprobs: Float[Tensor, "batch d_vocab"],
no_repeat_ngram_size: int | None,
k: int,
) -> tuple[Float[Tensor, "k"], Int[Tensor, "k"]]:
"""
logprobs:
tensor of the log-probs for the next token
no_repeat_ngram_size:
size of ngram to avoid repeating
k:
number of top logits to return, for each beam in our collection
Returns:
equivalent to the output of logprobs.topk(dim=-1), but makes sure that no returned tokens would produce an
ngram of size no_repeat_ngram_size which has already appeared in self.tokens.
"""
batch, seq_len = self.tokens.shape
# If completion isn't long enough for a repetition, or we have no restrictions, just return topk
if (no_repeat_ngram_size is not None) and (seq_len > no_repeat_ngram_size - 1):
# Otherwise, we need to check for ngram repetitions
# First, get the most recent no_repeat_ngram_size-1 tokens
last_ngram_prefix = self.tokens[:, seq_len - (no_repeat_ngram_size - 1) :]
# Next, find all the tokens we're not allowed to generate, by checking all past ngrams for a match
for i in range(seq_len - (no_repeat_ngram_size - 1)):
ngrams = self.tokens[:, i : i + no_repeat_ngram_size] # (batch, ngram)
ngrams_are_repeated = (ngrams[:, :-1] == last_ngram_prefix).all(-1) # (batch,)
ngram_end_tokens = ngrams[:, [-1]] # (batch, 1)
# Fill logprobs with neginf wherever the ngrams are repeated
logprobs[range(batch), ngram_end_tokens] = t.where(
ngrams_are_repeated, -1.0e4, logprobs[range(batch), ngram_end_tokens]
)
# Finally, get our actual tokens
return logprobs.topk(k=k, dim=-1)
Solution
def generate(self, k: int, no_repeat_ngram_size: int | None = None) -> "Beams":
"""
Starting from the current set of beams (i.e. self.tokens) and returns a new set of len(self.tokens) * k beams,
containing the best k continuations for each of the original beams.
Optional argument no_repeat_ngram_size means your model won't generate any sequences with a repeating n-gram
of this length.
"""
# Get the output logprobs for the next token (for every sequence in current beams)
logprobs = self.model(self.tokens)[:, -1, :].log_softmax(-1)
# Get the top toks_per_beam tokens for each sequence
topk_logprobs, topk_tokenIDs = self.get_topk_non_repeating(logprobs, no_repeat_ngram_size, k=k)
# Add new logprobs & concat new tokens. When doing this, we need to add an extra k dimension since our current
# logprobs & tokens have shape (batch,) and (batch, seq), but our new ones both have shape (batch, k)
new_logprob_sums = einops.repeat(self.logprob_sums, "b -> b k", k=k) + topk_logprobs
new_tokens = t.concat([einops.repeat(self.tokens, "b s -> b k s", k=k), topk_tokenIDs.unsqueeze(-1)], dim=-1)
return Beams(self.model, self.tokenizer, new_logprob_sums.flatten(), new_tokens.flatten(0, 1))
def filter(self, k: int) -> tuple["Beams", "Beams"]:
"""
Returns:
best_beams: Beams
filtered version of self, containing all best k which are also not terminated.
early_terminations: Beams
filtered version of self, containing all best k which are also terminated.
"""
# Get the indices of top k beams
top_beam_indices = self.logprob_sums.topk(k=k, dim=0).indices.tolist()
# Get the indices of terminated sequences
new_tokens = self.tokens[:, -1]
terminated_indices = t.nonzero(new_tokens == self.tokenizer.eos_token_id)
# Get the indices of the k best sequences (some terminated, some not terminated)
best_continuing = [i for i in top_beam_indices if i not in terminated_indices]
best_terminated = [i for i in top_beam_indices if i in terminated_indices]
# Return the beam objects from these indices
return self[best_continuing], self[best_terminated]
def get_topk_non_repeating(
self,
logprobs: Float[Tensor, "batch d_vocab"],
no_repeat_ngram_size: int | None,
k: int,
) -> tuple[Float[Tensor, "k"], Int[Tensor, "k"]]:
"""
logprobs:
tensor of the log-probs for the next token
no_repeat_ngram_size:
size of ngram to avoid repeating
k:
number of top logits to return, for each beam in our collection
Returns:
equivalent to the output of logprobs.topk(dim=-1), but makes sure that no returned tokens would produce an
ngram of size no_repeat_ngram_size which has already appeared in self.tokens.
"""
batch, seq_len = self.tokens.shape
# If completion isn't long enough for a repetition, or we have no restrictions, just return topk
if (no_repeat_ngram_size is not None) and (seq_len > no_repeat_ngram_size - 1):
# Otherwise, we need to check for ngram repetitions
# First, get the most recent no_repeat_ngram_size-1 tokens
last_ngram_prefix = self.tokens[:, seq_len - (no_repeat_ngram_size - 1) :]
# Next, find all the tokens we're not allowed to generate, by checking all past ngrams for a match
for i in range(seq_len - (no_repeat_ngram_size - 1)):
ngrams = self.tokens[:, i : i + no_repeat_ngram_size] # (batch, ngram)
ngrams_are_repeated = (ngrams[:, :-1] == last_ngram_prefix).all(-1) # (batch,)
ngram_end_tokens = ngrams[:, [-1]] # (batch, 1)
# Fill logprobs with neginf wherever the ngrams are repeated
logprobs[range(batch), ngram_end_tokens] = t.where(
ngrams_are_repeated, -1.0e4, logprobs[range(batch), ngram_end_tokens]
)
# Finally, get our actual tokens
return logprobs.topk(k=k, dim=-1)
Example usage of the Beams class, and the print method, corresponding to the diagram above:
# Start with prompt "When I was", get top 3 tokens (and their logprobs), and use that to create & display the top 3 beams
prompt = "When I was"
tokens = tokenizer.encode(prompt, return_tensors="pt").to(device)
logprobs = model(tokens)[0, -1].log_softmax(-1)
top_logprobs, top_tokens = logprobs.topk(k=3, dim=-1)
new_tokens = t.concat([tokens.repeat(3, 1), top_tokens.unsqueeze(-1)], dim=-1)
beams = Beams(model, tokenizer, logprob_sums=top_logprobs, tokens=new_tokens)
beams.print()
Best completions ┏━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━┓ ┃ logprob sum ┃ completion ┃ ┡━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━┩ │ -2.393 │ 'When I was a' │ │ -2.556 │ 'When I was in' │ │ -3.168 │ 'When I was growing' │ └─────────────┴──────────────────────┘
And here are some unit tests for your generate and filter methods, starting from the prompt "When I was" (so your output should match the diagram above).
print("Testing generate...")
new_beams = beams.generate(k=3, no_repeat_ngram_size=1)
new_beams.print()
expected_values = [
(-3.1, "When I was a kid"),
(-4.8, "When I was a child"),
(-4.9, "When I was a little"),
]
for i, (logprob_sum, completion) in enumerate(new_beams.logprobs_and_completions[:3]):
assert abs(logprob_sum - expected_values[i][0]) < 0.1, f"{i}"
assert completion == expected_values[i][1], f"{i}"
print("All tests for `generate` passed!")
Best completions ┏━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ logprob sum ┃ completion ┃ ┡━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ -3.091 │ 'When I was a kid' │ │ -4.808 │ 'When I was a child' │ │ -4.916 │ 'When I was a little' │ │ -4.611 │ 'When I was in the' │ │ -4.671 │ 'When I was in college' │ │ -5.140 │ 'When I was in high' │ │ -3.181 │ 'When I was growing up' │ │ -9.352 │ 'When I was growing older' │ │ -10.004 │ 'When I was growing my' │ └─────────────┴────────────────────────────┘
print("Testing `filter`...")
best_beams, terminated_beams = new_beams.filter(3)
best_beams.print()
expected_values = [
(-3.1, "When I was a kid"),
(-3.2, "When I was growing up"),
(-4.6, "When I was in the"),
]
for i, (logprob_sum, completion) in enumerate(best_beams.logprobs_and_completions):
assert abs(logprob_sum - expected_values[i][0]) < 0.1, f"{i}"
assert completion == expected_values[i][1], f"{i}"
assert len(terminated_beams.logprobs_and_completions) == 0
print("All tests for `filter` passed!")
Best completions ┏━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ logprob sum ┃ completion ┃ ┡━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ -3.091 │ 'When I was a kid' │ │ -3.181 │ 'When I was growing up' │ │ -4.611 │ 'When I was in the' │ └─────────────┴─────────────────────────┘
Lastly, we'll test the no_repeat_ngram_size argument. We do this by continually generating new tokens from our starting beams beams, and seeing if the model repeats the I was ngram (which it will by default unless we prohibit repeating n-grams).
print("Testing `no_repeat_ngram_size`...")
new_beams = beams
for _ in range(5):
new_beams = new_beams.generate(k=1)
new_beams.print(title="Completions with no ngram restriction")
assert all(
"I was" in completion.removeprefix(prompt)
for _, completion in new_beams.logprobs_and_completions
), "Without restriction, all beams should be completed as '...I was...'"
new_beams = beams
for _ in range(5):
new_beams = new_beams.generate(k=1, no_repeat_ngram_size=2)
new_beams.print(title="Completions with no repeated bigrams")
assert all(
"I was" not in completion.removeprefix(prompt)
for _, completion in new_beams.logprobs_and_completions
), "With no repeated bigrams, no beams should contain a second '...I was...'"
Completions with no ngram restriction ┏━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ logprob sum ┃ completion ┃ ┡━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ -9.144 │ 'When I was a kid, I was always' │ │ -10.811 │ 'When I was in the hospital, I was' │ │ -9.121 │ 'When I was growing up, I was always' │ └─────────────┴───────────────────────────────────────┘
Completions with no repeated bigrams ┏━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ logprob sum ┃ completion ┃ ┡━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ -8.650 │ 'When I was a kid, I would go' │ │ -11.909 │ 'When I was in the hospital, I saw' │ │ -9.043 │ 'When I was growing up, I would go' │ └─────────────┴─────────────────────────────────────┘
Once you've passed all of these unit tests, you can try implementing the full beam search function. It should create a Beams object from the initial prompt, and then repeatedly call generate and filter until the stopping criteria are met.
sampler = TransformerSampler(model, tokenizer)
prompt = "The ships hung in the sky in much the same way that"
orig_len = len(tokenizer.encode(prompt))
final_logitsums_and_completions = sampler.beam_search(
prompt=prompt,
num_return_sequences=3,
num_beams=40,
max_new_tokens=60,
no_repeat_ngram_size=2,
)
# Print all the best output
for logprob_sum, text in final_logitsums_and_completions:
avg_logprob_as_prob = t.tensor(logprob_sum / (len(tokenizer.encode(text)) - orig_len)).exp()
rprint(f"Avg token prob = {avg_logprob_as_prob:.3f}\nBest output:\n[bold dark_orange]{text}")
Click to see the expected output (you might not get identical results depending on the exact details of your implementation)
Avg token prob = 0.255 Best output: The ships hung in the sky in much the same way that they did at the beginning of the Second World War. For the first time in history, the U.S. Navy was able to carry out a full-scale amphibious assault on a large number of targets in a short period of time. In doing so, it allowed the Navy toAvg token prob = 0.254 Best output: The ships hung in the sky in much the same way that they did at the beginning of the Second World War.
For the first time in history, the U.S. Navy was able to carry out a full-scale amphibious assault on a large number of targets in a short period of time. It was a major victory for the United StatesAvg token prob = 0.254 Best output: The ships hung in the sky in much the same way that they did at the beginning of the Second World War.
For the first time in history, the U.S. Navy was able to carry out a full-scale amphibious assault on a large number of targets in a short period of time. In fact, it was only a matter of
KV Caching
This section is also designed to be challenging, and take quite some time. There are many different ways to solve it, and you're expected to try and find your own way (you should think about this for a while before looking at the suggestions in the dropdowns). Additionally, you might not find it as interesting as some of the other sections. In this case, and if you have a lot of extra time, you might want to start on the "building BERT" exercises from this chapter.
How can caching help us?
The text generation we've done so far is needlessly re-computing certain values, which is very noticeable when you try to generate longer sequences.
Suppose you're generating text, and you've already run GPT on the sentence "My life motto:". Now you want to run the model on the sentence "My life motto: Always". Which computations from the first sentence can you reuse?
Answer
At each attention layer, the only things the attention layer needs from the previous sequence positions are the key and value vectors. This is explained in the following diagram, which compares the attention layer with and without caching (it's a big diagram so you might want to open it in a separate window to zoom in).
Exercise - implement KV caching
Modify your GPT-2 to optionally use a cache. When you run your GPT on "My life motto:", it should store the necessary values in the cache. Then in the next forward pass with just " Always" as input, it should load the cached values instead of recomputing them (and update the cache). This only needs to work with a single input sequence (batch size of 1), and you can assume that after the first forward pass, the input will be just one token.
The design of the cache is completely up to you - discuss possible designs with your partner before writing code. It should be possible to have only one GPT2 instance and many different cache instances at one time. Imagine that you want to use one instance to serve multiple users submitting requests for text generation like in AI Dungeon.
You'll also need to rewrite parts of your DemoTransformer code, in order to get this to work. The tests have been built to accommodate modules which return their output as the first element in a tuple (i.e. (output, cache)) rather than just returning the output, so you should use the tests to verify that your modules still work as expected.
Some example considerations:
- Which GPT-2 classes need to interact with the cache?
- Will you need to change the positional embedding, and if so then how?
- Should the cache be mutable and be updated in place, or does updating actually just create a separate instance?
- (Hint here - think about how you might use the cache during beam search.)
- Is it possible for other programmers to incorrectly use your cache? Is there a way to prevent this failure mode or at least detect this and complain loudly?
Cache implentation (example)
This KeyValueCache object is structured as just a fancy tensor (it inherits all the methods from Tensor). The main difference is that it has a few extra helper methods, e.g. constructing an empty cache from a Config object.
There are other ways you could do this, e.g. having your KeyValueCache class contain list of KeyValueCacheEntry objects (where each of these corresponds to a different layer).
# Define a type for a single layer's cache entry (useful for type checking in later functions)
KeyValueCacheTensor = Float[Tensor, "2 batch seq_len n_heads d_head"]
class KeyValueCache(Tensor):
'''
This class holds tensors of key and value vectors, to be used for caching.
If we define it using cfg and batch then it's initialized as empty, but
we can also define it from kv_cache_entries.
'''
@classmethod
def new_empty(cls, cfg: Config, batch: int = 1) -> "KeyValueCache":
'''
Doing a forward pass on a cache created in this way indicates "we don't
yet have a cache, but we want this forward pass to return a cache".
Whereas using cache=None in a forward pass indicates we don't want to
return a cache.
'''
shape = (cfg.n_layers, 2, batch, 0, cfg.n_heads, cfg.d_head)
return cls(*shape).to(device)
# Define a handful of properties, so they can be referenced directly rather than
# indexing (which is more likely to lead to mistakes)
@property
def k(self) -> Tensor:
return self[:, 0]
@property
def v(self) -> Tensor:
return self[:, 1]
@property
def batch(self) -> int:
return self.shape[2]
@property
def seq_len(self) -> int:
return self.shape[3]
# Example implementation:
cfg = model.cfg
batch = 6
kv_cache = KeyValueCache.new_empty(cfg, batch)
print(f"Shape of all kv-cache = {tuple(kv_cache.shape)}")
print(f"Shape of just k-cache = {tuple(kv_cache.k.shape)}")
for kv_cache_entry in kv_cache:
print(f"Shape of cache entry for one layer = {tuple(kv_cache_entry.shape)}")
break
print(f"Batch size = {kv_cache.batch}")
print(f"Current sequence length = {kv_cache.seq_len}")
New DemoTransformer components (and testing)
# Define new model parts where necessary, and create a new model & test it
# Note that sometimes our modules return a tuple of (tensor output, cache) rather than just output. The
# tests have been built to accommodate this.
class PosEmbed(nn.Module):
def __init__(self, cfg: Config):
super().__init__()
self.cfg = cfg
self.W_pos = nn.Parameter(t.empty((cfg.n_ctx, cfg.d_model)))
nn.init.normal_(self.W_pos, std=self.cfg.init_range)
def forward(
self,
tokens: Int[Tensor, "batch position"],
past_kv_pos_offset: int = 0
) -> Float[Tensor, "batch position d_model"]:
batch, seq_len = tokens.shape
return einops.repeat(
self.W_pos[past_kv_pos_offset: seq_len+past_kv_pos_offset],
"seq d_model -> batch seq d_model",
batch=batch
)
class Attention(nn.Module):
IGNORE: Float[Tensor, ""]
def __init__(self, cfg: Config):
super().__init__()
self.cfg = cfg
self.W_Q = nn.Parameter(t.empty((cfg.n_heads, cfg.d_model, cfg.d_head)))
self.W_K = nn.Parameter(t.empty((cfg.n_heads, cfg.d_model, cfg.d_head)))
self.W_V = nn.Parameter(t.empty((cfg.n_heads, cfg.d_model, cfg.d_head)))
self.W_O = nn.Parameter(t.empty((cfg.n_heads, cfg.d_head, cfg.d_model)))
self.b_Q = nn.Parameter(t.zeros((cfg.n_heads, cfg.d_head)))
self.b_K = nn.Parameter(t.zeros((cfg.n_heads, cfg.d_head)))
self.b_V = nn.Parameter(t.zeros((cfg.n_heads, cfg.d_head)))
self.b_O = nn.Parameter(t.zeros((cfg.d_model)))
nn.init.normal_(self.W_Q, std=self.cfg.init_range)
nn.init.normal_(self.W_K, std=self.cfg.init_range)
nn.init.normal_(self.W_V, std=self.cfg.init_range)
nn.init.normal_(self.W_O, std=self.cfg.init_range)
self.register_buffer("IGNORE", t.tensor(-1e5, dtype=t.float32, device=device))
def forward(
self,
normalized_resid_pre: Float[Tensor, "batch posn d_model"],
kv_cache_entry: KeyValueCacheTensor | None = None,
) -> tuple[
Float[Tensor, "batch posn d_model"],
KeyValueCacheTensor | None
]:
'''
Returns the result of applying attention layer to normlized_resid_pre, as well as
the new cached key and value vectors (which we get from concatenating the old cached
ones with the new key and value vectors).
'''
# Calculate the new query, key and value vectors
q = einops.einsum(
normalized_resid_pre, self.W_Q,
"batch posn d_model, nheads d_model d_head -> batch posn nheads d_head"
) + self.b_Q
k = einops.einsum(
normalized_resid_pre, self.W_K,
"batch posn d_model, nheads d_model d_head -> batch posn nheads d_head"
) + self.b_K
v = einops.einsum(
normalized_resid_pre, self.W_V,
"batch posn d_model, nheads d_model d_head -> batch posn nheads d_head"
) + self.b_V
# If cache_entry is not None, this means we use the previous key and value vectors
# Also we'll need to get a new cache entry which will be used later to construct a new cache
if kv_cache_entry is not None:
k = t.concat([kv_cache_entry[0], k], dim=1)
v = t.concat([kv_cache_entry[1], v], dim=1)
kv_cache_entry = t.stack([k, v])
# Calculate attention scores, then scale and mask, and apply softmax to get probabilities
attn_scores = einops.einsum(
q, k,
"batch posn_Q nheads d_head, batch posn_K nheads d_head -> batch nheads posn_Q posn_K"
)
attn_scores_masked = self.apply_causal_mask(attn_scores / self.cfg.d_head ** 0.5)
attn_pattern = attn_scores_masked.softmax(-1)
# Take weighted sum of value vectors, according to attention probabilities
z = einops.einsum(
v, attn_pattern,
"batch posn_K nheads d_head, batch nheads posn_Q posn_K -> batch posn_Q nheads d_head"
)
# Calculate output (by applying matrix W_O and summing over heads, then adding bias b_O)
out = einops.einsum(
z, self.W_O,
"batch posn_Q nheads d_head, nheads d_head d_model -> batch posn_Q d_model"
) + self.b_O
return out, kv_cache_entry
def apply_causal_mask(
self, attn_scores: Float[Tensor, "batch n_heads query_pos key_pos"]
) -> Float[Tensor, "batch n_heads query_pos key_pos"]:
'''
Here, attn_scores have shape (batch, n_heads, query_pos, key_pos), where query_pos represents the
new (non-cached) positions, and key_pos represent all the positions (cached and non-cached).
So when we create our mask, the query indices and key indices will both go up to the same value
(the full sequence length), but the query indices will start at >0.
'''
new_seq_len, full_seq_len = attn_scores.shape[-2:]
assert new_seq_len <= full_seq_len
q_posn = einops.repeat(attn_scores.new_tensor(range(full_seq_len-new_seq_len, full_seq_len)), "q -> q k", k=full_seq_len)
k_posn = einops.repeat(attn_scores.new_tensor(range(full_seq_len)), "k -> q k", q=new_seq_len)
mask = q_posn < k_posn
attn_scores = attn_scores.masked_fill(mask, self.IGNORE)
return attn_scores
class TransformerBlock(nn.Module):
def __init__(self, cfg: Config):
super().__init__()
self.cfg = cfg
self.ln1 = LayerNorm(cfg)
self.attn = Attention(cfg)
self.ln2 = LayerNorm(cfg)
self.mlp = MLP(cfg)
def forward(
self,
resid_pre: Float[Tensor, "batch position d_model"],
kv_cache_entry: KeyValueCacheTensor | None = None,
) -> Float[Tensor, "batch position d_model"]:
attn_out, kv_cache_entry = self.attn(self.ln1(resid_pre), kv_cache_entry)
resid_mid = attn_out + resid_pre
resid_post = self.mlp(self.ln2(resid_mid)) + resid_mid
return resid_post, kv_cache_entry
class DemoTransformer(nn.Module):
def __init__(self, cfg: Config):
super().__init__()
self.cfg = cfg
self.embed = Embed(cfg)
self.pos_embed = PosEmbed(cfg)
self.blocks = nn.ModuleList([TransformerBlock(cfg) for _ in range(cfg.n_layers)])
self.ln_final = LayerNorm(cfg)
self.unembed = Unembed(cfg)
def forward(
self,
tokens: Int[Tensor, "batch seq_pos"],
kv_cache: KeyValueCache | None = None
) -> Float[Tensor, "batch position d_vocab"]:
using_kv_cache = kv_cache is not None
if using_kv_cache:
# If using kv_cache, then we only need to pass forward the newest tokens
# Remember to add positional offset!
n_cached_tokens = kv_cache.seq_len
tokens = tokens[:, n_cached_tokens:]
residual = self.embed(tokens) + self.pos_embed(tokens, n_cached_tokens)
else:
# If not using cache, turn it into a list of None's (so we can iterate through it)
kv_cache = [None for _ in range(self.cfg.n_layers)]
residual = self.embed(tokens) + self.pos_embed(tokens)
# Apply all layers, and create a (new) kv_cache from the key & value vectors
new_kv_cache_entries: list[KeyValueCacheTensor] = []
for block, kv_cache_entry in zip(self.blocks, kv_cache):
residual, kv_cache_entry = block(residual, kv_cache_entry)
if using_kv_cache: new_kv_cache_entries.append(kv_cache_entry)
logits = self.unembed(self.ln_final(residual))
if using_kv_cache:
return logits, KeyValueCache(t.stack(new_kv_cache_entries))
else:
return logits, None
tokens = reference_gpt2.to_tokens(reference_text).to(device)
logits, cache = reference_gpt2.run_with_cache(tokens)
rand_int_test(PosEmbed, [2, 4])
load_gpt2_test(PosEmbed, reference_gpt2.pos_embed, tokens)
rand_float_test(Attention, [2, 4, 768])
load_gpt2_test(Attention, reference_gpt2.blocks[0].attn, cache["normalized", 0, "ln1"])
rand_float_test(TransformerBlock, [2, 4, 768])
load_gpt2_test(TransformerBlock, reference_gpt2.blocks[0], cache["resid_pre", 0])
rand_int_test(DemoTransformer, [2, 4])
load_gpt2_test(DemoTransformer, reference_gpt2, tokens)
New sampling function
@t.inference_mode()
def sample_with_cache(
self: TransformerSampler,
prompt: str,
max_tokens_generated=100,
kv_cache: KeyValueCache | None = None,
verbose=False,
seed: int | None = None,
kwargs
) -> str:
self.model.eval()
input_ids = self.tokenizer.encode(prompt, return_tensors="pt").to(device)[0]
if seed is not None:
np.random.seed(seed)
t.manual_seed(seed)
for i in tqdm(range(max_tokens_generated)):
# Get new logits (make sure we don't pass in more tokens than the model's context length)
logits, kv_cache = self.model(input_ids[None, -self.cfg.n_ctx:], kv_cache)
# We only take logits for the last token, because this is what we're sampling
logits = logits[0, -1]
# Get next token (as a tensor of size (1, 1) so we can concat it to input_ids)
next_token = t.tensor([TransformerSampler.sample_next_token(input_ids, logits, kwargs)], device=device)
# Create new input ids string, with shape (1, old_seq_len + 1)
input_ids = t.cat([input_ids, next_token], dim=-1)
# Print out results, if required
if verbose:
print(self.tokenizer.decode(input_ids), end="\r")
# If our new token was the end-of-text token, stop
if next_token == getattr(self.tokenizer, "eos_token_id", None):
break
return self.tokenizer.decode(input_ids)
TransformerSampler.sample = sample_with_cache
Code to verify that the same output is being produced by cache and no-cache versions (and to compare speeds)
device = t.device("cuda") # can also try "cpu"
model = DemoTransformer(Config()).to(device)
model.load_state_dict(reference_gpt2.state_dict(), strict=False);
initial_text = "Eliezer Shlomo Yudkowsky (born September 11, 1979) is an American decision and artificial intelligence (AI) theorist and writer, best known for"
# input_ids = tokenizer.encode(initial_text, return_tensors="pt").squeeze()
sampler = TransformerSampler(model, tokenizer)
# Run the noncached version
t0 = time.time()
text = sampler.sample(
initial_text,
temperature=0.7,
top_p=0.95,
seed=0,
)
print(f"Time taken (without cache): {time.time() - t0:.2f} seconds")
rprint(f"Model output:\n\n[bold dark_orange]{text}[/]")
# Run the cached version
t0 = time.time()
text_with_cache = sampler.sample(
initial_text,
temperature=0.7,
top_p=0.95,
seed=0,
kv_cache=KeyValueCache.new_empty(sampler.cfg)
)
print(f"Time taken (with cache): {time.time() - t0:.2f} seconds")
rprint(f"Model output:\n\n[bold dark_orange]{text_with_cache}[/]")
# # Check they are the same
assert text == text_with_cache, "Your outputs are different, meaning you've probably made a mistake in your cache implementation (or failed to use random seeds)."
print("Tests passed!")
You may find that your cache implementation provides a modest speedup, but probably not close to the seq_len-factor speedup you'd expect from the fact that you only compute one additional token at each step rather than all of them. Why is this? The answer is that, much like everything to do with computational and memory costs in deep learning, it's not so simple. There are a host of different factors which might be bottlenecking our model's forward pass speed. If you try this on the CPU, you should get a much more noticeable speedup.
For a bit more on these topics, see here.
Bonus - cached beam search
Can you modify your beam search function to use caching?
Depending on how you implemented your cache earlier, you might find that a different form of caching is better suited to beam search.
Again, we've provided an example implementation in a dropdown below, which is based on the cache implementation above and the previous solution for beam_search.
Cached beam search function
As we touched on earlier, thanks to our modular code, not a lot needs to be changed when adding cache support.
@dataclass
class Beams:
'''Class to store beams during beam search.'''
model: DemoTransformer
tokenizer: GPT2TokenizerFast
logprob_sums: Float[Tensor, "batch"]
tokens: Int[Tensor, "batch seq"]
kv_cache: KeyValueCache | None = None
def __getitem__(self, idx) -> "Beams":
'''Helpful function allowing you to take a slice of the beams object along the batch dimension.'''
return Beams(
self.model,
self.tokenizer,
self.logprob_sums[idx],
self.tokens[idx],
self.kv_cache[:, :, idx] if self.kv_cache is not None else None
)
@property
def logprobs_and_completions(self) -> list[tuple[float, str]]:
'''Returns self as a list of logprob sums and completions (useful for getting final output).'''
return [
(logprob_sum.item(), self.tokenizer.decode(tokens))
for (logprob_sum, tokens) in zip(self.logprob_sums, self.tokens)
]
def generate(self, k: int, no_repeat_ngram_size: int | None = None) -> "Beams":
'''
Starting from the current set of beams (i.e. self.tokens) and returns a new set of len(self.tokens) k beams,
containing the best k continuations for each of the original beams.
Optional argument no_repeat_ngram_size means your model won't generate any sequences with a repeating n-gram
of this length.
'''
# Get the output logprobs for the next token (for every sequence in current beams)
logprobs, kv_cache = self.model(self.tokens, self.kv_cache)
logprobs = logprobs[:, -1, :].log_softmax(-1)
# Get the top toks_per_beam tokens for each sequence
topk_logprobs, topk_tokenIDs = self.get_topk_non_repeating(logprobs, no_repeat_ngram_size, k=k)
# Add new logprobs & concat new tokens. When doing this, we need to add an extra k dimension since our current
# logprobs & tokens have shape (batch,) and (batch, seq), but our new ones both have shape (batch, k)
new_logprob_sums = einops.repeat(self.logprob_sums, "b -> b k", k=k) + topk_logprobs
new_tokens = t.concat([einops.repeat(self.tokens, "b s -> b k s", k=k), topk_tokenIDs.unsqueeze(-1)], dim=-1)
return Beams(self.model, self.tokenizer, new_logprob_sums.flatten(), new_tokens.flatten(0, 1), new_kv_cache)
def filter(self, k: int) -> tuple["Beams", "Beams"]:
'''
Returns:
best_beams: Beams
filtered version of self, containing all best k which are also not terminated.
early_terminations: Beams
filtered version of self, containing all best k which are also terminated.
'''
# Get the indices of top k beams
top_beam_indices = self.logprob_sums.topk(k=k, dim=0).indices.tolist()
# Get the indices of terminated sequences
new_tokens = self.tokens[:, -1]
terminated_indices = t.nonzero(new_tokens == self.tokenizer.eos_token_id)
# Get the indices of the k best sequences (some terminated, some not terminated)
best_continuing = [i for i in top_beam_indices if i not in terminated_indices]
best_terminated = [i for i in top_beam_indices if i in terminated_indices]
# Return the beam objects from these indices
return self[best_continuing], self[best_terminated]
def get_topk_non_repeating(
self,
logprobs: Float[Tensor, "batch d_vocab"],
no_repeat_ngram_size: int | None,
k: int,
) -> tuple[Float[Tensor, "k"], Int[Tensor, "k"]]:
"""
logprobs:
tensor of the log-probs for the next token
no_repeat_ngram_size:
size of ngram to avoid repeating
k:
number of top logits to return, for each beam in our collection
Returns:
equivalent to the output of logprobs.topk(dim=-1), but makes sure that no returned tokens would produce an
ngram of size no_repeat_ngram_size which has already appeared in self.tokens.
"""
batch, seq_len = self.tokens.shape
# If completion isn't long enough for a repetition, or we have no restrictions, just return topk
if (no_repeat_ngram_size is not None) and (seq_len > no_repeat_ngram_size - 1):
# Otherwise, we need to check for ngram repetitions
# First, get the most recent no_repeat_ngram_size-1 tokens
last_ngram_prefix = self.tokens[:, seq_len - (no_repeat_ngram_size - 1) :]
# Next, find all the tokens we're not allowed to generate, by checking all past ngrams for a match
for i in range(seq_len - (no_repeat_ngram_size - 1)):
ngrams = self.tokens[:, i : i + no_repeat_ngram_size] # (batch, ngram)
ngrams_are_repeated = (ngrams[:, :-1] == last_ngram_prefix).all(-1) # (batch,)
ngram_end_tokens = ngrams[:, [-1]] # (batch, 1)
# Fill logprobs with neginf wherever the ngrams are repeated
logprobs[range(batch), ngram_end_tokens] = t.where(
ngrams_are_repeated, -1.0e4, logprobs[range(batch), ngram_end_tokens]
)
# Finally, get our actual tokens
return logprobs.topk(k=k, dim=-1)
def print(self, title="Best completions", max_print_chars=80) -> None:
'''
Prints out a set of sequences with their corresponding logitsums.
'''
if len(self.tokens) == 0:
return
table = Table("logitsum", "completion", title=title)
for logprob_sum, tokens in zip(self.logprob_sums, self.tokens):
text = self.tokenizer.decode(tokens)
if len(repr(text)) > max_print_chars:
text = text[:int(0.3 max_print_chars)] + " ... " + text[-int(0.7 * max_print_chars):]
table.add_row(f"{logprob_sum:>8.3f}", repr(text))
rprint(table)
@t.inference_mode()
def beam_search(
self,
prompt: str,
num_return_sequences: int,
num_beams: int,
max_new_tokens: int,
no_repeat_ngram_size: int | None = None,
kv_cache: KeyValueCache | None = None,
) -> list[tuple[float, Tensor]]:
'''
Implements a beam search, by repeatedly performing the generate and filter steps (starting from the initial
prompt) until either of the two stopping criteria are met: (1) we've generated max_new_tokens tokens, or (2)
we've generated num_returns_sequences terminating sequences.
'''
assert num_return_sequences <= num_beams
self.model.eval()
tokens = self.tokenizer.encode(prompt, return_tensors="pt").to(device)
final_logprobs_and_completions = [] # we add to this list as we get terminated beams
best_beams = Beams(self.model, self.tokenizer, t.tensor([0.0]).to(device), tokens) # start with just 1 beam
for _ in tqdm(range(max_new_tokens)):
# Generate & filter beams
best_beams = best_beams.generate(k=num_beams, no_repeat_ngram_size=no_repeat_ngram_size)
best_beams, best_beams_terminated = best_beams.filter(k=num_beams)
# Add terminated beams to our list, and return early if we have enough
final_logprobs_and_completions.extend(best_beams_terminated.logprobs_and_completions)
if len(final_logprobs_and_completions) >= num_return_sequences:
return final_logprobs_and_completions[:num_return_sequences]
# Return terminated beams plus the best ongoing beams of length orig_len + max_new_tokens
final_logprobs_and_completions.extend(best_beams.logprobs_and_completions)
return final_logprobs_and_completions[:num_return_sequences]
Code to verify that the same output is being produced by cache and no-cache versions (and to compare speeds)
prompt = "For you, the day Bison graced your village was the most important day of your life. But for me, it was"
orig_len = len(tokenizer.encode(prompt))
beam_search_kwargs = dict(
prompt=prompt,
num_return_sequences=3,
num_beams=20,
max_new_tokens=60,
no_repeat_ngram_size=2,
verbose=False
)
sampler = TransformerSampler(model, tokenizer)
# Run the noncached version
t0 = time.time()
final_logitsums_and_completions = sampler.beam_search(beam_search_kwargs)
logprob_sum, text = final_logitsums_and_completions[0]
avg_logprob_as_prob = t.tensor(logprob_sum / (len(tokenizer.encode(text)) - orig_len)).exp().item()
print(f"Time (without cache): {time.time() - t0:.2f} seconds")
print(f"Avg logprob (expressed as a probability) = {avg_logprob_as_prob:.3f}")
rprint(f"Output:\n\n[bold dark_orange]{text}[/]\n\n")
# Run the cached version
t0 = time.time()
beam_search_kwargs["kv_cache"] = KeyValueCache.new_empty(model.cfg)
final_logitsums_and_completions = sampler.beam_search(beam_search_kwargs)
logprob_sum, text_with_cache = final_logitsums_and_completions[0]
avg_logprob_as_prob = t.tensor(logprob_sum / (len(tokenizer.encode(text)) - orig_len)).exp().item()
print(f"Time (with cache): {time.time() - t0:.2f} seconds")
print(f"Avg logprob (as probability) = {avg_logprob_as_prob:.3f}", end="")
rprint(f"Output:\n\n[bold dark_orange]{text_with_cache}[/]\n\n")
# Check they are the same
assert text == text_with_cache, "Your outputs are different, meaning you've probably made a mistake in your cache implementation."
print("Tests passed!")