3️⃣ Bonus - Transposed Convolutions

Learning Objectives

• Learn about & implement the transposed convolution operation.
• Implement GANs and/or VAEs entirely from scratch.

Transposed convolutions

In this section, we'll build all the modules required to implement our DCGAN.

Note - this section is similar in flavour to the bonus exercises from the "CNNs & ResNets" chapter, i.e. you'll be implementing transposed convolutions using low-level stride and tensor manipulation operations. That section should be considered a prerequisite for this one.

Now, what are transposed convolutions, and why should we care about them? One high-level intuition goes something like this: most of the generator's architecture is basically the discriminator architecture in reverse. We need something that performs the reverse of a convolution - not literally the inverse operation, but something reverse in spirit, which uses a kernel of weights to project up to some array of larger size.

Importantly, a transposed convolution isn't literally the inverse of a convolution. A lot of confusion can come from misunderstanding this!

You can describe the difference between convolutions and transposed convolutions as follows:

• In convolutions, you slide the kernel around inside the input. At each position of the kernel, you take a sumproduct between the kernel and that section of the input to calculate a single element in the output.
• In transposed convolutions, you slide the kernel around what will eventually be your output, and at each position you add some multiple of the kernel to your output.

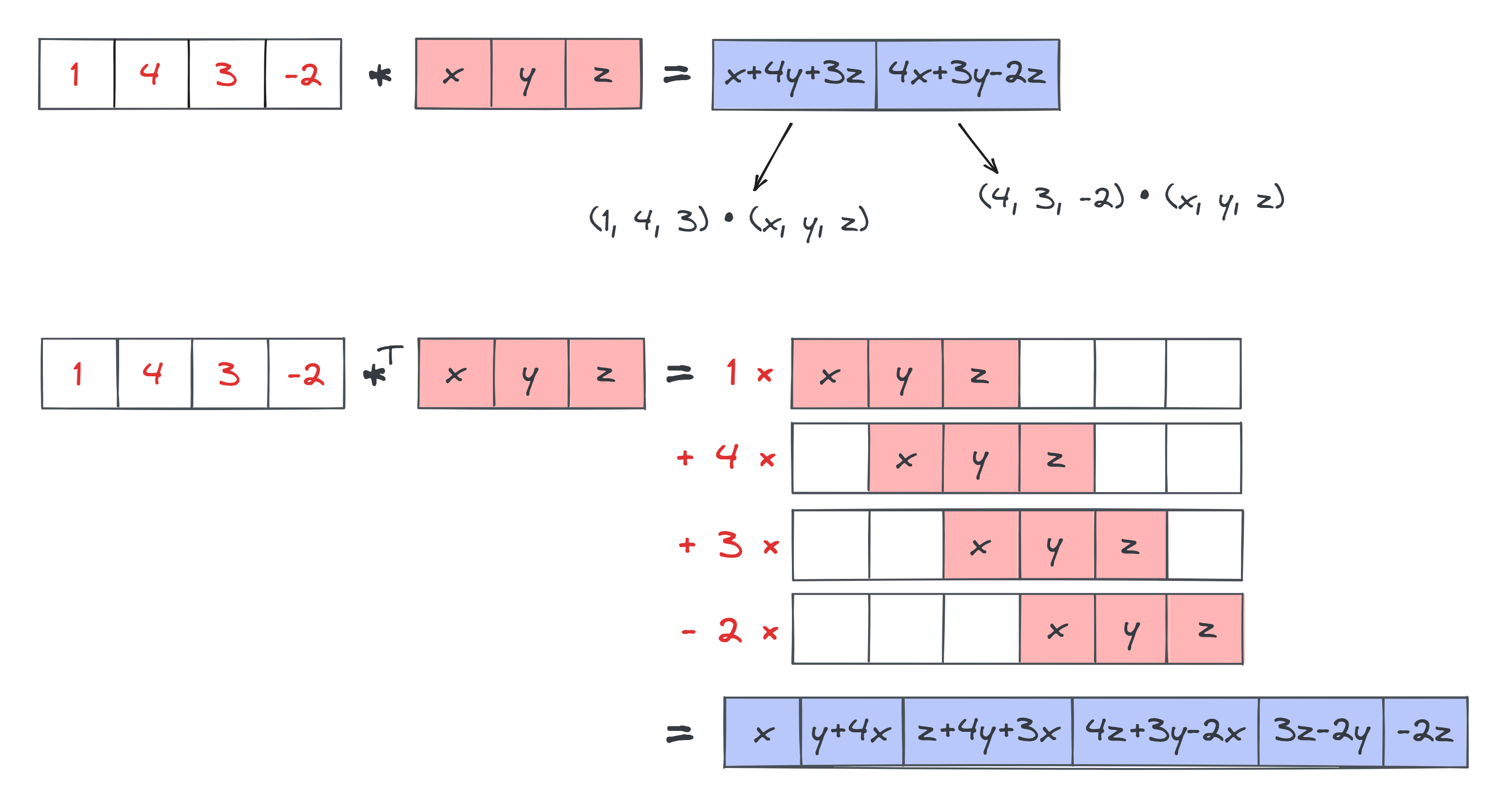
Below is an illustration of both for comparison, in the 1D case (where $*$ stands for the 1D convolution operator, and $*^T$ stands for the transposed convolution operator). Note the difference in size between the output in both cases. With standard convolutions, our output is smaller than our input, because we're having to fit the kernel inside the input in order to produce the output. But in our transposed convolutions, the output is actually larger than the input, because we're fitting the kernel inside the output.

Now, consider the elements in the output of the transposed convolution: z+4y+3x, 4x+3y-2x, etc. Note that these look a bit like convolutions, since they're inner products of slices of the input with versions of the kernel. This observation leads nicely into why transposed convolutions are called transposed convolutions - because they can actually be written as convolutions, just with a slightly modified input and kernel.

Question - how can this operation be cast as a convolution? In other words, exactly what arrays input and kernel would produce the same output as the transposed convolution above, if we performed a standard convolution on them?

From looking at the diagram, note that the final output (the blue row at the bottom) looks a bit like sliding the _reversed_ kernel over the input. In other words, we get elements like z+4y+3x which are an inner product between the input slice input[:3] = [1, 4, 3] and the reversed kernel [z, y, x]. This suggests we should be using the reversed kernel in our convolution.

Can we just use a reversed kernel on our original input and call it a day? No, because the output size wouldn't be correct. Using a reversed kernel on our original input would give us just the two elements [z+4y+3x, 4z+3y-2x], not the full 6-element output we actually get. The answer is that we need to pad out our input with zeros on the left and right, with the padding amount equal to kernel_size - 1.

To conclude - with input_modified = pad(input, kernel_size-1) and kernel_modified = kernel[::-1], we get:

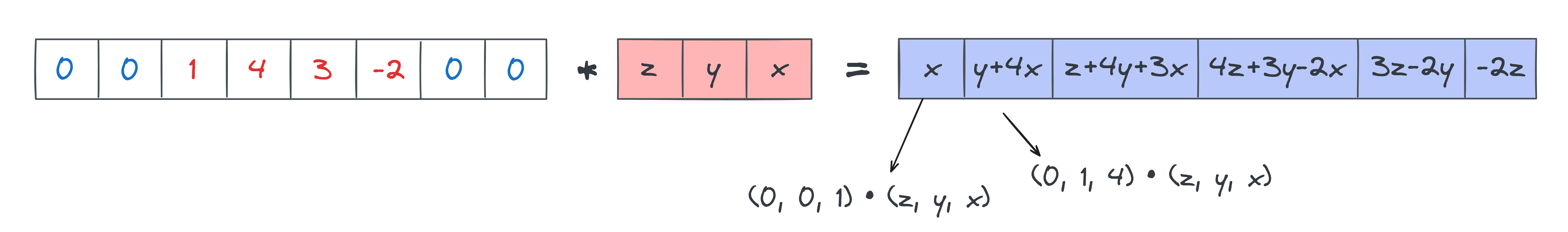
Note - it's also valid to say we use the original kernel and pad & flip the input, but for the exercises below we'll stick to the former interpretation.

Exercise - minimal 1D transposed convolutions

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 15-25 minutes on this exercise. ```

Now, you should implement the function conv_transpose1d_minimal. You're allowed to call functions like conv1d_minimal and pad1d which you wrote previously (if you didn't do these exercises, then you can import the solution versions of them - although we do recommend doing the conv from scratch exercises before these ones).

One important note - in our convolutions we assumed the kernel had shape (out_channels, in_channels, kernel_width). Here, the order is different: in_channels comes before out_channels.

from part2_cnns.solutions import (
    IntOrPair,
    conv1d_minimal,
    conv2d_minimal,
    force_pair,
    pad1d,
    pad2d,
)


def conv_transpose1d_minimal(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "in_channels out_channels kernel_width"],
) -> Float[Tensor, "batch out_channels output_width"]:
    """Like torch's conv_transpose1d using bias=False and all other keyword arguments left at their default values."""
    raise NotImplementedError()


tests.test_conv_transpose1d_minimal(conv_transpose1d_minimal)

from part2_cnns.solutions import (
    IntOrPair,
    conv1d_minimal,
    conv2d_minimal,
    force_pair,
    pad1d,
    pad2d,
)
def conv_transpose1d_minimal(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "in_channels out_channels kernel_width"],
) -> Float[Tensor, "batch out_channels output_width"]:
    """Like torch's conv_transpose1d using bias=False and all other keyword arguments left at their default values."""
    batch, in_channels, width = x.shape
    in_channels_2, out_channels, kernel_width = weights.shape
    assert in_channels == in_channels_2, "in_channels for x and weights don't match up"
x_mod = pad1d(x, left=kernel_width - 1, right=kernel_width - 1, pad_value=0)
    weights_mod = einops.rearrange(weights.flip(-1), "i o w -> o i w")
return conv1d_minimal(x_mod, weights_mod)

Exercise - 1D transposed convolutions

```yaml Difficulty: 🔴🔴🔴🔴🔴 Importance: 🔵🔵⚪⚪⚪

You should spend up to 25-40 minutes on this exercise. ```

Now we add in the extra parameters padding and stride, just like we did for our convolutions back in week 0.

The basic idea is that both parameters mean the inverse of what they did in for convolutions.

In convolutions, padding tells you how much to pad the input by. But in transposed convolutions, we pad the input by kernel_size - 1 - padding (recall that we're already padding by kernel_size - 1 by default). So padding decreases our output size rather than increasing it.

In convolutions, stride tells you how much to step the kernel by, as it's being moved around inside the input. In transposed convolutions, stride does something different: you space out all your input elements by an amount equal to stride before performing your transposed convolution. This might sound strange, but it's actually equivalent to performing strides as you're moving the kernel around inside the output. This diagram should help show why:

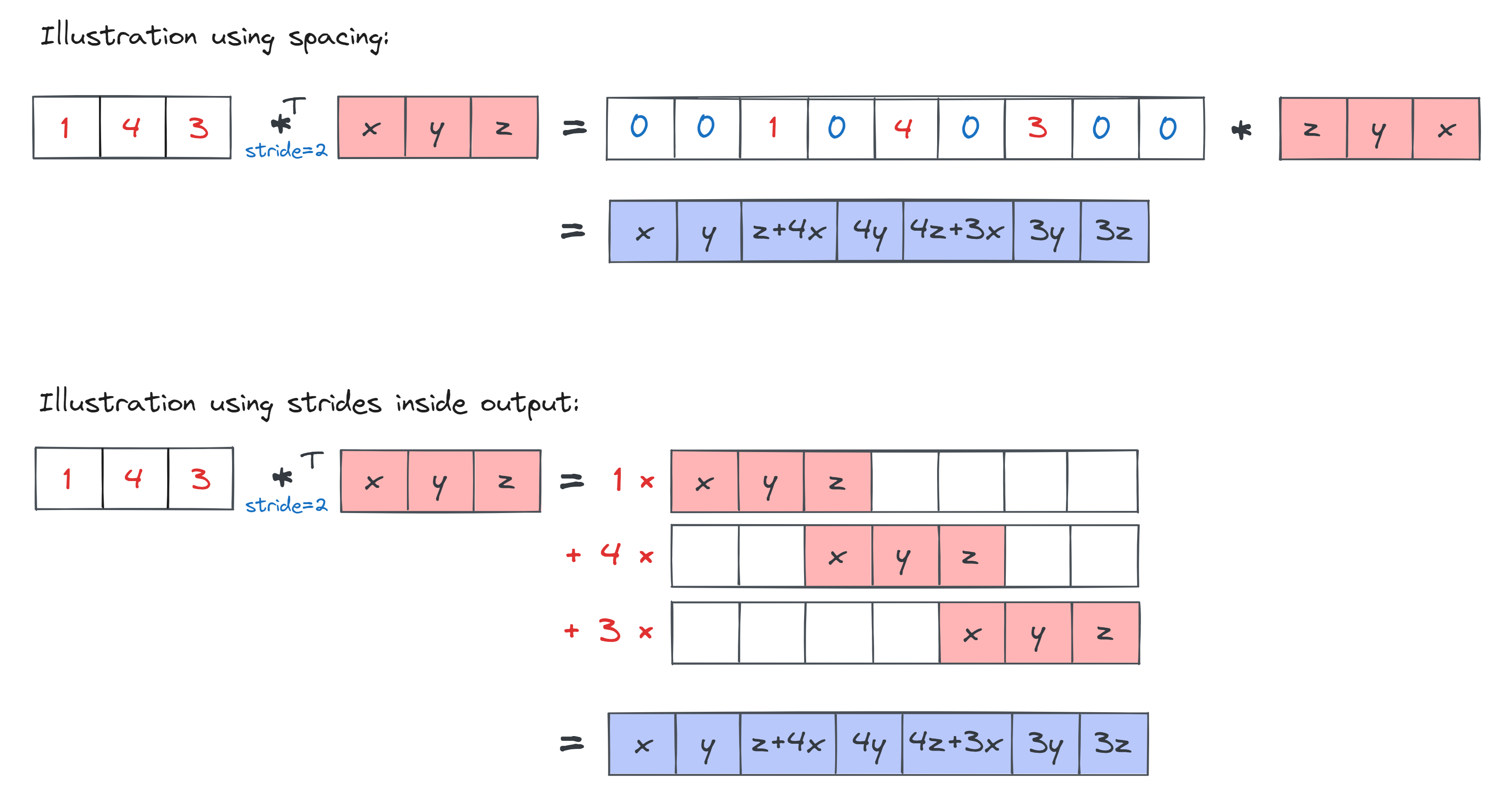
For this reason, transposed convolutions are also referred to as fractionally strided convolutions, since a stride of 2 over the output is equivalent to a 1/2 stride over the input (i.e. every time the kernel takes two steps inside the spaced-out version of the input, it moves one stride with reference to the original input).

Question - what is the formula relating output size, input size, kernel size, stride and padding? (note, you shouldn't need to refer to this explicitly in your functions)

output_size = input_size + kernel_size - 1

output_size = input_size + kernel_size - 1 - 2  padding

output_size = (input_size - 1)  stride + kernel_size - 2  padding

Padding should be pretty easy for you to implement on top of what you've already done. For strides, you will need to construct a strided version of the input which is "spaced out" in the way described above, before performing the transposed convolution. It might help to write a fractional_stride function; we've provided the code for you to do this.

def fractional_stride_1d(
    x: Float[Tensor, "batch in_channels width"], stride: int = 1
) -> Float[Tensor, "batch in_channels output_width"]:
    """
    Returns a version of x suitable for transposed convolutions, i.e. "spaced out" with zeros
    between its values. This spacing only happens along the last dimension.

    x: shape (batch, in_channels, width)

    Example:
        x = [[[1, 2, 3], [4, 5, 6]]]
        stride = 2
        output = [[[1, 0, 2, 0, 3], [4, 0, 5, 0, 6]]]
    """
    raise NotImplementedError()


tests.test_fractional_stride_1d(fractional_stride_1d)

def fractional_stride_1d(
    x: Float[Tensor, "batch in_channels width"], stride: int = 1
) -> Float[Tensor, "batch in_channels output_width"]:
    """
    Returns a version of x suitable for transposed convolutions, i.e. "spaced out" with zeros
    between its values. This spacing only happens along the last dimension.
    x: shape (batch, in_channels, width)
    Example:
        x = [[[1, 2, 3], [4, 5, 6]]]
        stride = 2
        output = [[[1, 0, 2, 0, 3], [4, 0, 5, 0, 6]]]
    """
    batch, in_channels, width = x.shape
    width_new = width + (stride - 1) * (
        width - 1
    )  # the RHS of this sum is the number of zeros we need to add between elements
    x_new_shape = (batch, in_channels, width_new)
# Create an empty array to store the spaced version of x in.
    x_new = t.zeros(size=x_new_shape, dtype=x.dtype, device=x.device)
x_new[..., ::stride] = x
return x_new

def conv_transpose1d(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "in_channels out_channels kernel_width"],
    stride: int = 1,
    padding: int = 0,
) -> Float[Tensor, "batch out_channels output_width"]:
    """
    Like torch's conv_transpose1d using bias=False and all other keyword arguments left at their
    default values.
    """
    raise NotImplementedError()


tests.test_conv_transpose1d(conv_transpose1d)

def conv_transpose1d(
    x: Float[Tensor, "batch in_channels width"],
    weights: Float[Tensor, "in_channels out_channels kernel_width"],
    stride: int = 1,
    padding: int = 0,
) -> Float[Tensor, "batch out_channels output_width"]:
    """
    Like torch's conv_transpose1d using bias=False and all other keyword arguments left at their
    default values.
    """
    batch, ic, width = x.shape
    ic_2, oc, kernel_width = weights.shape
    assert ic == ic_2, (
        f"in_channels for x and weights don't match up. Shapes are {x.shape}, {weights.shape}."
    )
# Apply spacing
    x_spaced_out = fractional_stride_1d(x, stride)
# Apply modification (which is controlled by the padding parameter)
    padding_amount = kernel_width - 1 - padding
    assert padding_amount >= 0, "total amount padded should be positive"
    x_mod = pad1d(x_spaced_out, left=padding_amount, right=padding_amount, pad_value=0)
# Modify weights, then return the convolution
    weights_mod = einops.rearrange(weights.flip(-1), "i o w -> o i w")
return conv1d_minimal(x_mod, weights_mod)

Another fun fact about transposed convolutions - they are also called backwards strided convolutions, because they are equivalent to taking the gradient of Conv2d with respect to its output. As an optional bonus, can you formally prove this?

Exercise - 2D transposed convolutions

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵⚪⚪⚪⚪

You should spend up to 10-20 minutes on this exercise. ```

Finally, we get to 2D transposed convolutions! Since there's no big conceptual difference between this and the 1D case, we'll jump straight to implementing the full version of these convolutions, with padding and strides. A few notes:

• You'll need to make fractional_stride_2d, which performs spacing along the last two dimensions rather than just the last dimension.
• Defining the modified version of your kernel will involve reversing on more than one dimension. You'll still need to perform the same rearrangement flipping the output and input channel dimensions though.
• You can use the force_pair function from earlier this week (it's been imported for you, as have the Pair and IntOrPair types).

def fractional_stride_2d(
    x: Float[Tensor, "batch in_channels height width"], stride_h: int, stride_w: int
) -> Float[Tensor, "batch in_channels output_height output_width"]:
    """
    Same as fractional_stride_1d, except we apply it along the last 2 dims of x (height and width).
    """
    raise NotImplementedError()


def conv_transpose2d(x, weights, stride: IntOrPair = 1, padding: IntOrPair = 0) -> Tensor:
    """Like torch's conv_transpose2d using bias=False
    x: shape (batch, in_channels, height, width)
    weights: shape (out_channels, in_channels, kernel_height, kernel_width)
    Returns: shape (batch, out_channels, output_height, output_width)
    """
    raise NotImplementedError()


tests.test_fractional_stride_2d(fractional_stride_2d)
tests.test_conv_transpose2d(conv_transpose2d)

def fractional_stride_2d(
    x: Float[Tensor, "batch in_channels height width"], stride_h: int, stride_w: int
) -> Float[Tensor, "batch in_channels output_height output_width"]:
    """
    Same as fractional_stride_1d, except we apply it along the last 2 dims of x (height and width).
    """
    batch, in_channels, height, width = x.shape
    width_new = width + (stride_w - 1)  (width - 1)
    height_new = height + (stride_h - 1)  (height - 1)
    x_new_shape = (batch, in_channels, height_new, width_new)
# Create an empty array to store the spaced version of x in.
    x_new = t.zeros(size=x_new_shape, dtype=x.dtype, device=x.device)
x_new[..., ::stride_h, ::stride_w] = x
return x_new
def conv_transpose2d(x, weights, stride: IntOrPair = 1, padding: IntOrPair = 0) -> Tensor:
    """Like torch's conv_transpose2d using bias=False
    x: shape (batch, in_channels, height, width)
    weights: shape (out_channels, in_channels, kernel_height, kernel_width)
    Returns: shape (batch, out_channels, output_height, output_width)
    """
    stride_h, stride_w = force_pair(stride)
    padding_h, padding_w = force_pair(padding)
batch, ic, height, width = x.shape
    ic_2, oc, kernel_height, kernel_width = weights.shape
    assert ic == ic_2, (
        f"in_channels for x and weights don't match up. Shapes are {x.shape}, {weights.shape}."
    )
# Apply spacing
    x_spaced_out = fractional_stride_2d(x, stride_h, stride_w)
# Apply modification (which is controlled by the padding parameter)
    pad_h_actual = kernel_height - 1 - padding_h
    pad_w_actual = kernel_width - 1 - padding_w
    assert min(pad_h_actual, pad_w_actual) >= 0, "total amount padded should be positive"
    x_mod = pad2d(
        x_spaced_out,
        left=pad_w_actual,
        right=pad_w_actual,
        top=pad_h_actual,
        bottom=pad_h_actual,
        pad_value=0,
    )
# Modify weights
    weights_mod = einops.rearrange(weights.flip(-1, -2), "i o h w -> o i h w")
# Return the convolution
    return conv2d_minimal(x_mod, weights_mod)

Exercise - transposed conv module

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵⚪⚪⚪

You should spend up to 10-15 minutes on this exercise. ```

Now that you've written a function to calculate the convolutional transpose, you should implement it as a module just like you've done for Conv2d previously. Your weights should be initialised with the uniform distribution Unif[-sqrt(k), sqrt(k)] where k = 1 / (out_channels * kernel_width * kernel_height) (this is PyTorch's standard behaviour for convolutional transpose layers).

class ConvTranspose2d(nn.Module):
    def __init__(
        self,
        in_channels: int,
        out_channels: int,
        kernel_size: IntOrPair,
        stride: IntOrPair = 1,
        padding: IntOrPair = 0,
    ):
        """
        Same as torch.nn.ConvTranspose2d with bias=False.
        Name your weight field `self.weight` for compatibility with the tests.
        """
        super().__init__()

        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = force_pair(kernel_size)
        self.stride = stride
        self.padding = padding

        raise NotImplementedError()

    def forward(
        self, x: Float[Tensor, "batch in_channels height width"]
    ) -> Float[Tensor, "batch out_channels output_height output_width"]:
        raise NotImplementedError()

    def extra_repr(self) -> str:
        keys = ["in_channels", "out_channels", "kernel_size", "stride", "padding"]
        return ", ".join([f"{key}={getattr(self, key)}" for key in keys])


tests.test_ConvTranspose2d(ConvTranspose2d)

class ConvTranspose2d(nn.Module):
    def __init__(
        self,
        in_channels: int,
        out_channels: int,
        kernel_size: IntOrPair,
        stride: IntOrPair = 1,
        padding: IntOrPair = 0,
    ):
        """
        Same as torch.nn.ConvTranspose2d with bias=False.
        Name your weight field self.weight for compatibility with the tests.
        """
        super().__init__()
self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = force_pair(kernel_size)
        self.stride = stride
        self.padding = padding
sf = 1 / (self.out_channels  self.kernel_size[0]  self.kernel_size[1]) ** 0.5
        self.weight = nn.Parameter(
            sf  (2  t.rand(in_channels, out_channels, *self.kernel_size) - 1)
        )
def forward(
        self, x: Float[Tensor, "batch in_channels height width"]
    ) -> Float[Tensor, "batch out_channels output_height output_width"]:
        return conv_transpose2d(x, self.weight, self.stride, self.padding)
def extra_repr(self) -> str:
        keys = ["in_channels", "out_channels", "kernel_size", "stride", "padding"]
        return ", ".join([f"{key}={getattr(self, key)}" for key in keys])

Now, you're all done! You can go back and implement GANs or VAEs using the transposed convolution module you've just written.