2️⃣ GANs
Learning Objectives
- Understand the loss function used in GANs, and why it can be expected to result in the generator producing realistic outputs.
- Implement the DCGAN architecture from the paper, with relatively minimal guidance.
- Learn how to identify and fix bugs in your GAN architecture, to improve convergence properties.
Reading
- Google Machine Learning Education, Generative Adversarial Networks (strongly recommended, ~15 mins)
- This is a very accessible introduction to the core ideas behind GANs
- You should read at least the sections in Overview, and the sections in GAN Anatomy up to and including Loss Functions
- Unsupervised representation learning with deep convolutional generative adversarial networks (optional, we'll be going through parts of this paper later on in the exercises)
- This paper introduced the DCGAN, and describes an architecture very close to the one we'll be building today.
- It's one of the most cited ML papers of all time!
How GANs work
The basic idea behind GANs is as follows:
- You have two networks, the generator and the discriminator.
- The generator's job is to produce output realistic enough to fool the discriminator, and the discriminator's job is to try and tell the difference between real and fake output.
The idea is for both networks to be trained simultaneously, in a positive feedback loop: as the generator produces better output, the discriminator's job becomes harder, and it has to learn to spot more subtle features distinguishing real and fake images, meaning the generator has to work harder to produce images with those features.
Discriminator
The discriminator works by taking an image (either real, or created by the generator), and outputting a single value between 0 and 1, which is the probability that the discriminator puts on the image being real. The discriminator sees the images, but not the labels (i.e. whether the images are real or fake), and it is trained to distinguish between real and fake images with maximum accuracy. The discriminator's loss function is the cross entropy between its probability estimates ($D(x)$ for real images, $D(G(z))$ for fake images) and the true labels ($1$ for real images, $0$ for fake images).
Generator
The architecture of generators in a GAN setup is generally a mirror image of the discriminator, with convolutions swapped out for transposed convolutions. This is the case for the DCGAN paper we'll be reading (which is why they only give a diagram of the generator, not both). The generator works by taking in a vector $z$, whose elements are all normally distributed with mean 0 and variance 1. We call the space from which $z$ is sampled latent dimension or latent space, and we call $z$ a latent vector. The formal definition of a latent space is an abstract multi-dimensional space that encodes a meaningful internal representation of externally observed events. We'll dive a little deeper into what this means and the overall significance of latent spaces later on, but for now it's fine to understand this vector $z$ as a kind of random seed, which causes the generator to produce different outputs. After all, if the generator only ever produced the same image as output then the discriminator's job would be pretty easy (just subtract the image $g$ always produces from the input image, and see if the result is close to zero!). The generator's objective function is an increasing function of $D(G(z))$, in other words it tries to produce images $G(z)$ which have a high chance of fooling the discriminator (i.e. $D(G(z)) \approx 1$).
Convergence
The ideal outcome when training a GAN is for the generator to produce perfect output indistinguishable from real images, and the discriminator just guesses randomly. However, the precise nature of the situations when GANs converge is an ongoing area of study (in general, adversarial networks have very unstable training patterns). For example, you can imagine a situation where the discriminator becomes almost perfect at spotting fake outputs, because of some feature that the discriminator spots and that the generator fails to capture in its outputs. It will be very difficult for the generator to get a training signal, because it has to figure out what feature is missing from its outputs, and how it can add that feature to fool the discriminator. And to make matters worse, maybe marginal steps in that direction will only increase the probability of fooling the discriminator from almost-zero to slightly-more-than-almost-zero, which isn't much of a training signal! Later on we will see techniques people have developed to overcome problems like this and others, but in general they can't be solved completely.
Optional exercise - what conditions must hold for the discriminator's best strategy to be random guessing with probability 0.5?
It is necessary for the generator to be producing perfect outputs, because otherwise the discriminator could do better than random guessing.
If the generator is producing perfect outputs, then the discriminator never has any ability to distinguish real from fake images, so it has no information. Its job is to minimise the cross entropy between its output distribution $(D(x), 1-D(x))$, and the distribution of real/fake images. Call this $(p, 1-p)$, i.e. $p$ stands for the proportion of images in training which are real. Note how we just used $p$ rather than $p(x)$, because there's no information in the image $x$ which indicates whether it is real or fake. Trying to minimize the cross entropy between $(p, 1-p)$ and $(D(x), 1-D(x))$ gives us the solution $D(x) = p$ for all $x$. In other words, our discriminator guesses real/fake randomly with probability equal to the true underlying frequency of real/fake images in the data. This is 0.5 if and only if the data contains an equal number of real and fake images.
To summarize, the necessary and sufficient conditions for $(\forall x) \; D(x) = 0.5$ being the optimal strategy are:
The generator $G$ produces perfect output The underlying frequency of real/fake images in the data is 50/50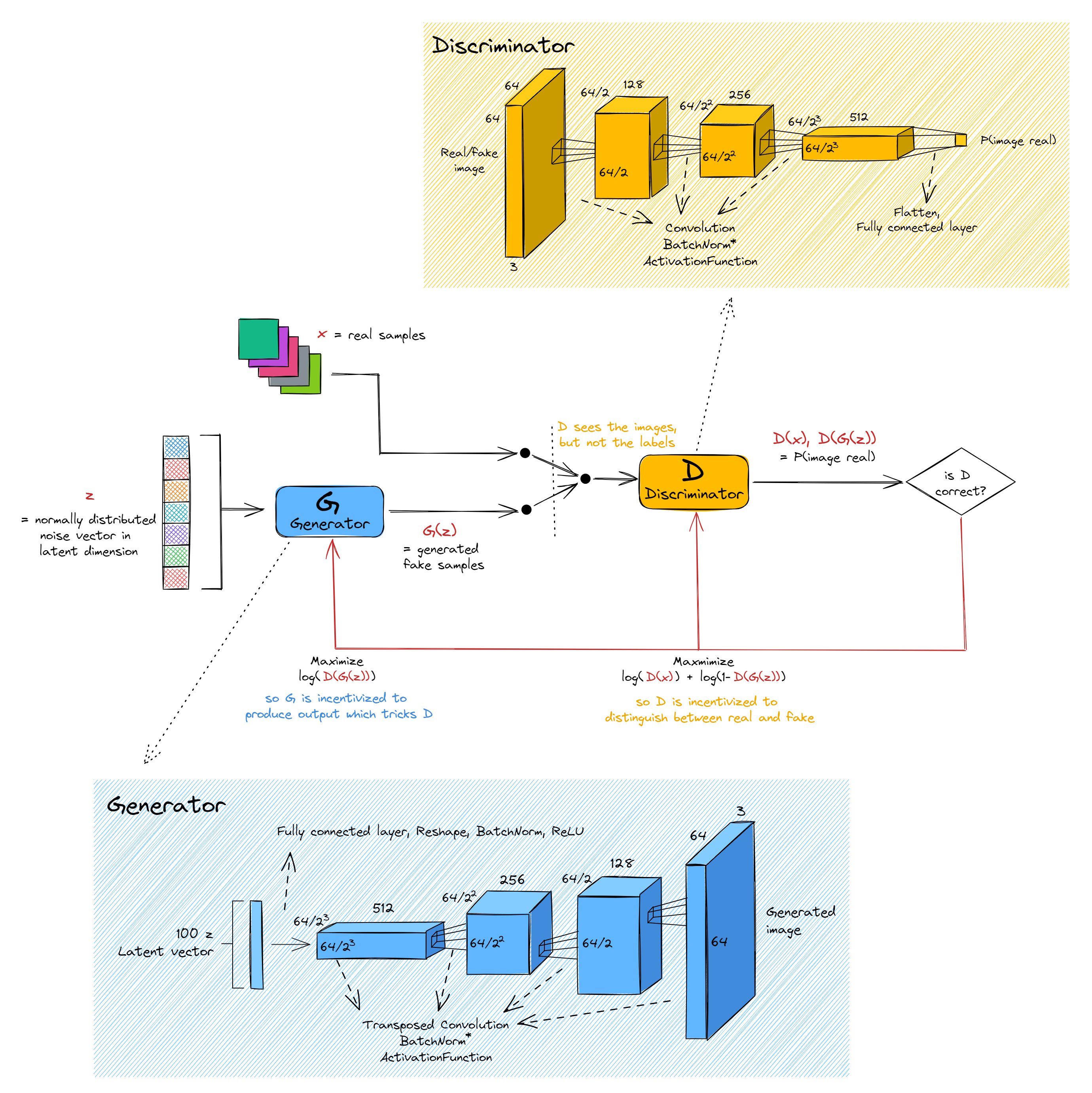
Exercise - some more modules
```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵⚪⚪⚪
You should spend up to 10-20 minutes on this exercise. ```
You'll also need to implement a few more modules, which have docstrings provided below (they should be fairly quick, and will just serve as a refresher for the structure of modules). They are:
Tanhwhich is an activation function used by the DCGAN you'll be implementing.LeakyReLUwhich is an activation function used by the DCGAN you'll be implementing. This function is popular in tasks where we we may suffer from sparse gradients (GANs are a primary example of this).Sigmoid, for converting the single logit output from the discriminator into a probability.
They should all be relatively short. You can go back to day 2's exercises to remind yourself of the basic syntax.
class Tanh(nn.Module):
def forward(self, x: Tensor) -> Tensor:
raise NotImplementedError()
class LeakyReLU(nn.Module):
def __init__(self, negative_slope: float = 0.01):
super().__init__()
self.negative_slope = negative_slope
def forward(self, x: Tensor) -> Tensor:
raise NotImplementedError()
def extra_repr(self) -> str:
return f"negative_slope={self.negative_slope}"
class Sigmoid(nn.Module):
def forward(self, x: Tensor) -> Tensor:
raise NotImplementedError()
tests.test_Tanh(Tanh)
tests.test_LeakyReLU(LeakyReLU)
tests.test_Sigmoid(Sigmoid)
Solution
class Tanh(nn.Module):
def forward(self, x: Tensor) -> Tensor:
return (t.exp(x) - t.exp(-x)) / (t.exp(x) + t.exp(-x))
class LeakyReLU(nn.Module):
def __init__(self, negative_slope: float = 0.01):
super().__init__()
self.negative_slope = negative_slope
def forward(self, x: Tensor) -> Tensor:
return t.where(x > 0, x, self.negative_slope * x)
def extra_repr(self) -> str:
return f"negative_slope={self.negative_slope}"
class Sigmoid(nn.Module):
def forward(self, x: Tensor) -> Tensor:
return 1 / (1 + t.exp(-x))
GANs
Now, you're ready to implement and train your own DCGAN! You'll be basing your implementation on the DCGAN paper. Implementing architectures based on descriptions in papers is an incredibly valuable skill for any would-be research engineer, however in these exercises we've given enough guidance on this page that you shouldn't need to refer to the paper much if at all. However, we do encourage you to skim the paper, and think about how you might go about this replication task without guidance!
Discriminator & Generator architectures
We refer back to the diagram at the start of this section for the basic discriminator and generator architectures. Rather than hardcoding a single set of values, we're going to make our architecture more flexible - giving us the ability to change the number of layers, or the sizes of each layer, by using different input arguments.
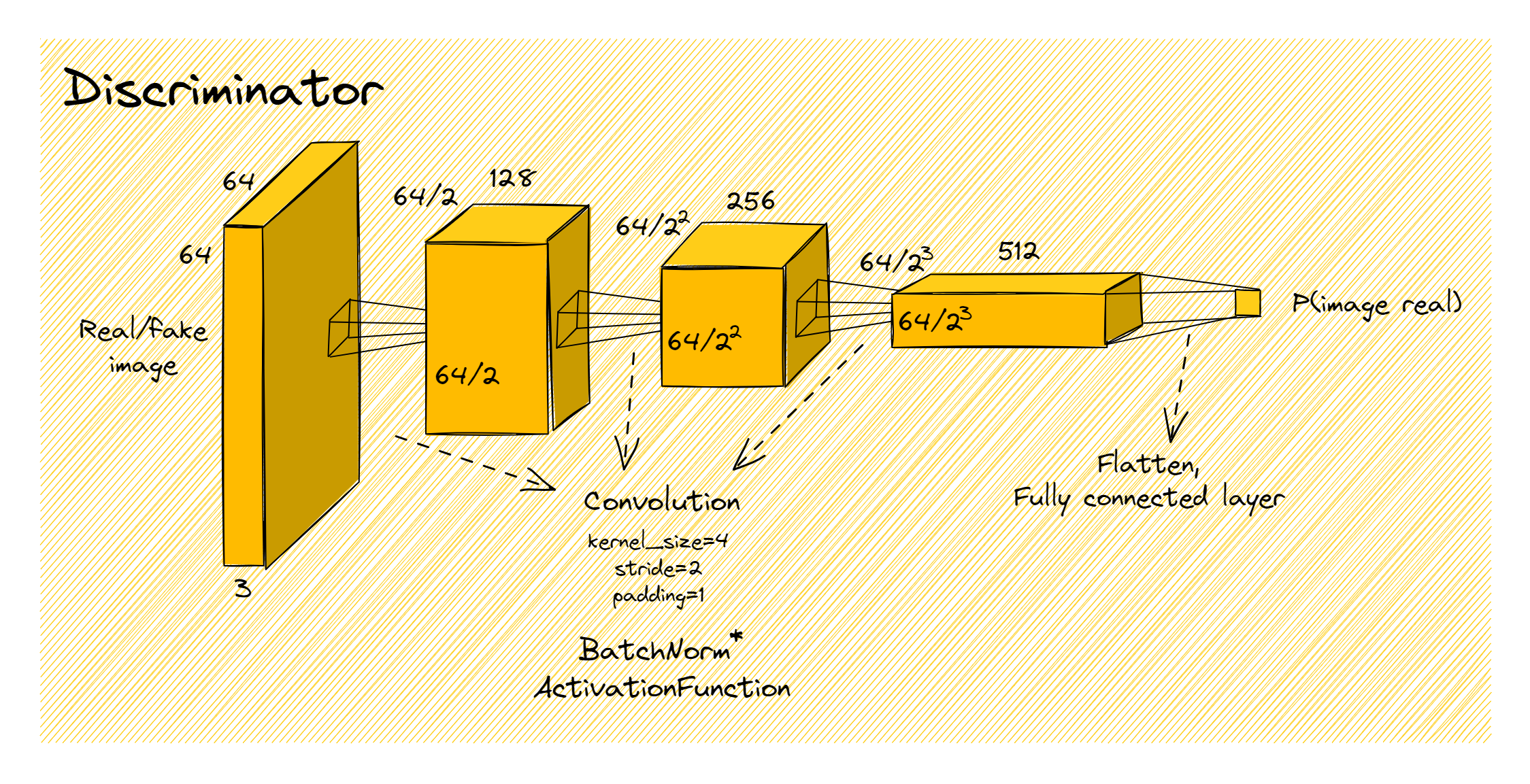
Discriminator
The discriminator starts with a series of blocks of the form (Conv -> BatchNorm -> ActivationFunction). Following the paper's conventions:
- Each convolution should have kernel size 4, stride 2, padding 1. This will halve the width and height of the image at each step. The output channels of each convolution are given by the
hidden_channelsargument. For instance, ifimg_channels=3(because the image is RGB) andhidden_channels=[128, 256, 512], then there will be three convolutions: the first mapping from 3 -> 128 channels, the second from 128 -> 256, and the third from 256 -> 512. - All blocks have a batchnorm layer, except for the very first one.
- All blocks' activation functions are
LeakyRelu.
Lastly, we flatten the output of the final convolutional block, and use a fully connected layer to map it to a single value (i.e. a vector of length batch_size) which we then pass through a sigmoid to get a probability that the image is real. Again, we recommend the Rearrange module from the einops library for this.
None of the convolutions or linear layers should have biases (this is also true for the generator).
The diagram below shows what we'd get with the following arguments:
img_size = 64
img_channels = 3
hidden_channels = [128, 256, 512]
Generator
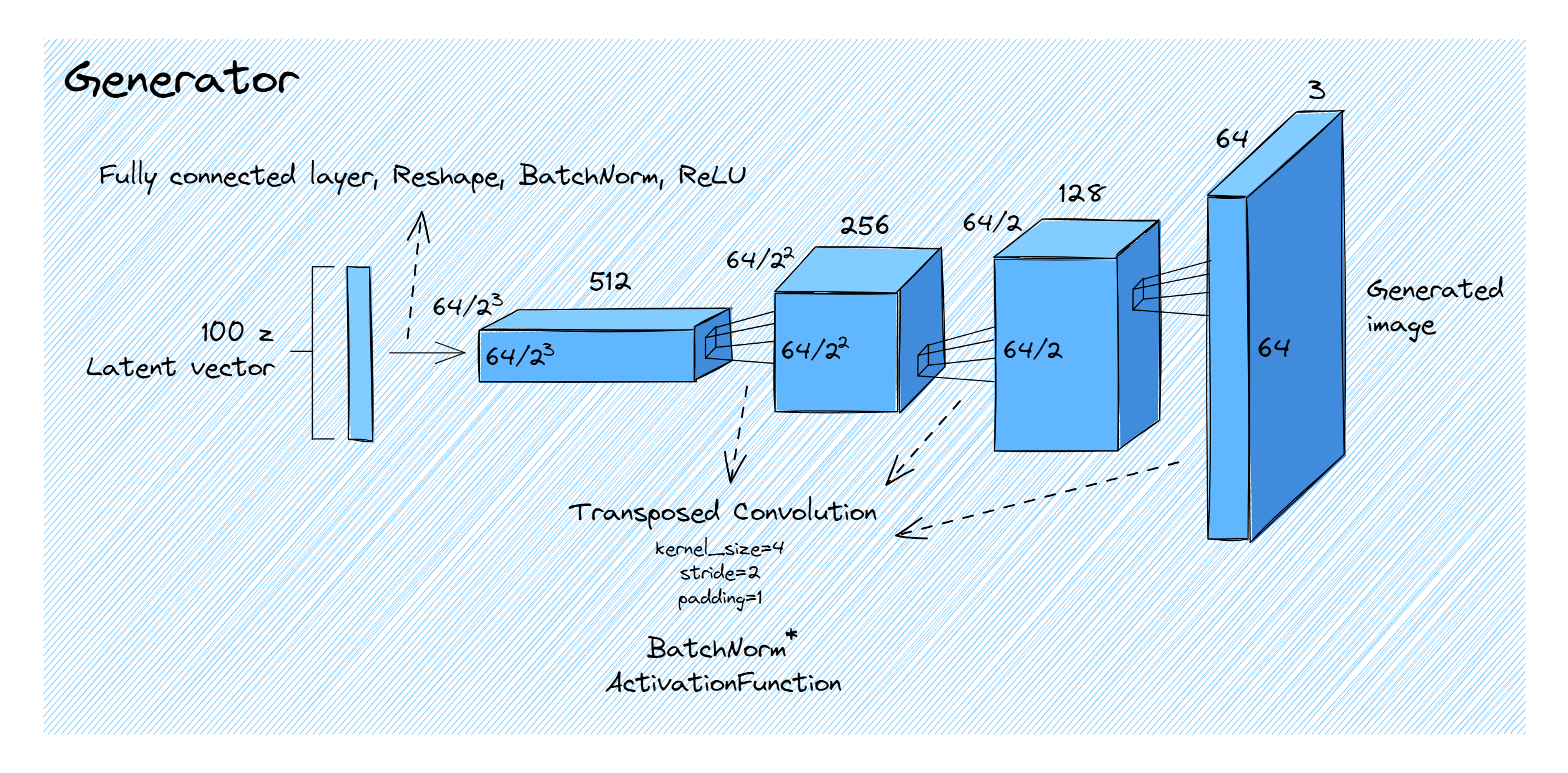
The generator is essentially the mirror image of the discriminator. While the discriminator had convolutions which halved the image size on each layer, the generator has transposed convolutions which double the size on each layer (so apart from the very start of the generator / end of the discriminator, all the activations have the same shape, just in reverse).
We start with the latent vector of shape (batch_size, latent_dim_size), and apply a fully connected layer & reshaping to get our first tensor which has shape (batch_size, channels, height, width). The parameters channels and height (which is equal to width) can be calculated from the img_size and hidden_channels arguments (remember that image size doubles at each transposed convolution, and after applying all the transposed convolutions we'll eventually get back to img_size). Then, we apply batchnorm and relu.
After this, we apply a series of blocks of the form (ConvTranspose -> BatchNorm -> ActivationFunction). Following the paper's conventions:
- Each transposed convolution has kernel size 4, stride 2, padding 1. Like for the discriminator, the input & output channels of the convolutions are determined by the
hidden_channelsargument (although this time they're in reverse order). - All blocks have a batchnorm layer, except for the very last one.
- All blocks' activation functions are
ReLU, except for the last one which isTanh.
The diagram below shows what we'd get with the following arguments:
img_size = 64
img_channels = 3
hidden_channels = [128, 256, 512]
latent_dim_size = 100
Exercise - building your GAN
```yaml Difficulty: 🔴🔴🔴🔴🔴 Importance: 🔵🔵🔵🔵⚪
You should spend up to 30-50 minutes on this exercise. ```
You should implement your code below. We've provided one possible design choice and the corresponding forward functions:
- The generator is made of an initial
project_and_reshapeblock that performs the first linear map, and thenhidden_layerswhich are a stack of blocks each consisting of a (transponsed convolution, optional batchnorm, activation fn). - The discriminator is made of
hidden_layerswhich are a stack of (convolution, optional batchnorm, activation fn) blocks, and a finalclassifierblock which flattens and maps to a single output (which represents the probability pre-sigmoid).
We've also given you the DCGAN class - note that we've not included a forward method here, because you'll usually be calling your discriminator and generators' forward methods directly. You can think of the DCGAN class as essentially a wrapper for both.
If you're stuck, you can import the generator and discriminator from the solutions, and compare it with yours. We've given you this option in place of test functions.
from part2_cnns.utils import print_param_count
print_param_count(Generator(), solutions.DCGAN().netG)
print_param_count(Discriminator(), solutions.DCGAN().netD)
Lastly, remember that torchinfo is a useful library for inspecting the architecture of your model. Since it works by running input through your model, it provides another useful way to check your model's architecture is correct (since errors like the wrong convolution size will often cause forward passes to fail).
model = DCGAN().to(device)
x = t.randn(3, 100).to(device)
print(torchinfo.summary(model.netG, input_data=x), end="\n\n")
print(torchinfo.summary(model.netD, input_data=model.netG(x)))
You can also check that the output of your model is the correct shape. Note - we're using a 3-layer model rather than the 4-layer model shown in the diagram and described the paper.
class Generator(nn.Module):
def __init__(
self,
latent_dim_size: int = 100,
img_size: int = 64,
img_channels: int = 3,
hidden_channels: list[int] = [128, 256, 512],
):
"""
Implements the generator architecture from the DCGAN paper (the diagram at the top
of page 4). We assume the size of the activations doubles at each layer (so image
size has to be divisible by 2 ** len(hidden_channels)).
Args:
latent_dim_size:
the size of the latent dimension, i.e. the input to the generator
img_size:
the size of the image, i.e. the output of the generator
img_channels:
the number of channels in the image (3 for RGB, 1 for grayscale)
hidden_channels:
the number of channels in the hidden layers of the generator (starting closest
to the middle of the DCGAN and going outward, i.e. in chronological order for
the generator)
"""
n_layers = len(hidden_channels)
assert img_size % (2**n_layers) == 0, "activation size must double at each layer"
super().__init__()
# self.project_and_reshape = ...
# self.hidden_layers = ...
def forward(self, x: Tensor) -> Tensor:
x = self.project_and_reshape(x)
x = self.hidden_layers(x)
return x
class Discriminator(nn.Module):
def __init__(
self,
img_size: int = 64,
img_channels: int = 3,
hidden_channels: list[int] = [128, 256, 512],
):
"""
Implements the discriminator architecture from the DCGAN paper (the mirror image of
the diagram at the top of page 4). We assume the size of the activations doubles at
each layer (so image size has to be divisible by 2 ** len(hidden_channels)).
Args:
img_size:
the size of the image, i.e. the input of the discriminator
img_channels:
the number of channels in the image (3 for RGB, 1 for grayscale)
hidden_channels:
the number of channels in the hidden layers of the discriminator (starting
closest to the middle of the DCGAN and going outward, i.e. in reverse-
chronological order for the discriminator)
"""
n_layers = len(hidden_channels)
assert img_size % (2**n_layers) == 0, "activation size must double at each layer"
super().__init__()
self.hidden_layers = ...
self.classifier = ...
def forward(self, x: Tensor) -> Tensor:
x = self.hidden_layers(x)
x = self.classifier(x)
return x.squeeze() # remove dummy `out_channels` dimension
class DCGAN(nn.Module):
netD: Discriminator
netG: Generator
def __init__(
self,
latent_dim_size: int = 100,
img_size: int = 64,
img_channels: int = 3,
hidden_channels: list[int] = [128, 256, 512],
):
super().__init__()
self.latent_dim_size = latent_dim_size
self.img_size = img_size
self.img_channels = img_channels
self.hidden_channels = hidden_channels
self.netD = Discriminator(img_size, img_channels, hidden_channels)
self.netG = Generator(latent_dim_size, img_size, img_channels, hidden_channels)
Solution
class Generator(nn.Module):
def __init__(
self,
latent_dim_size: int = 100,
img_size: int = 64,
img_channels: int = 3,
hidden_channels: list[int] = [128, 256, 512],
):
"""
Implements the generator architecture from the DCGAN paper (the diagram at the top
of page 4). We assume the size of the activations doubles at each layer (so image
size has to be divisible by 2 len(hidden_channels)).
Args:
latent_dim_size:
the size of the latent dimension, i.e. the input to the generator
img_size:
the size of the image, i.e. the output of the generator
img_channels:
the number of channels in the image (3 for RGB, 1 for grayscale)
hidden_channels:
the number of channels in the hidden layers of the generator (starting closest
to the middle of the DCGAN and going outward, i.e. in chronological order for
the generator)
"""
n_layers = len(hidden_channels)
assert img_size % (2n_layers) == 0, "activation size must double at each layer"
super().__init__()
# Reverse hidden channels, so they're in chronological order
hidden_channels = hidden_channels[::-1]
self.latent_dim_size = latent_dim_size
self.img_size = img_size
self.img_channels = img_channels
# Reverse them, so they're in chronological order for generator
self.hidden_channels = hidden_channels
# Define the first layer, i.e. latent dim -> (512, 4, 4) and reshape
first_height = img_size // (2**n_layers)
first_size = hidden_channels[0] * (first_height**2)
self.project_and_reshape = Sequential(
Linear(latent_dim_size, first_size, bias=False),
Rearrange("b (ic h w) -> b ic h w", h=first_height, w=first_height),
BatchNorm2d(hidden_channels[0]),
ReLU(),
)
# Equivalent, but using conv rather than linear:
# self.project_and_reshape = Sequential(
# Rearrange("b ic -> b ic 1 1"),
# solutions.ConvTranspose2d(latent_dim_size, hidden_channels[0], first_height, 1, 0),
# BatchNorm2d(hidden_channels[0]),
# ReLU(),
# )
# Get list of input & output channels for the convolutional blocks
in_channels = hidden_channels
out_channels = hidden_channels[1:] + [img_channels]
# Define all the convolutional blocks (conv_transposed -> batchnorm -> activation)
conv_layer_list = []
for i, (c_in, c_out) in enumerate(zip(in_channels, out_channels)):
conv_layer = [
ConvTranspose2d(c_in, c_out, 4, 2, 1),
ReLU() if i < n_layers - 1 else Tanh(),
]
if i < n_layers - 1:
conv_layer.insert(1, BatchNorm2d(c_out))
conv_layer_list.append(Sequential(conv_layer))
self.hidden_layers = Sequential(conv_layer_list)
def forward(self, x: Tensor) -> Tensor:
x = self.project_and_reshape(x)
x = self.hidden_layers(x)
return x
class Discriminator(nn.Module):
def __init__(
self,
img_size: int = 64,
img_channels: int = 3,
hidden_channels: list[int] = [128, 256, 512],
):
"""
Implements the discriminator architecture from the DCGAN paper (the mirror image of
the diagram at the top of page 4). We assume the size of the activations doubles at
each layer (so image size has to be divisible by 2 len(hidden_channels)).
Args:
img_size:
the size of the image, i.e. the input of the discriminator
img_channels:
the number of channels in the image (3 for RGB, 1 for grayscale)
hidden_channels:
the number of channels in the hidden layers of the discriminator (starting
closest to the middle of the DCGAN and going outward, i.e. in reverse-
chronological order for the discriminator)
"""
n_layers = len(hidden_channels)
assert img_size % (2n_layers) == 0, "activation size must double at each layer"
super().__init__()
self.img_size = img_size
self.img_channels = img_channels
self.hidden_channels = hidden_channels
# Get list of input & output channels for the convolutional blocks
in_channels = [img_channels] + hidden_channels[:-1]
out_channels = hidden_channels
# Define all the convolutional blocks (conv_transposed -> batchnorm -> activation)
conv_layer_list = []
for i, (c_in, c_out) in enumerate(zip(in_channels, out_channels)):
conv_layer = [
Conv2d(c_in, c_out, 4, 2, 1),
LeakyReLU(0.2),
]
if i > 0:
conv_layer.insert(1, BatchNorm2d(c_out))
conv_layer_list.append(Sequential(conv_layer))
self.hidden_layers = Sequential(conv_layer_list)
# Define the last layer, i.e. reshape and (512, 4, 4) -> real/fake classification
final_height = img_size // (2**n_layers)
final_size = hidden_channels[-1] * (final_height**2)
self.classifier = Sequential(
Rearrange("b c h w -> b (c h w)"),
Linear(final_size, 1, bias=False),
Sigmoid(),
)
# Equivalent, but using conv rather than linear:
# self.classifier = Sequential(
# Conv2d(out_channels[-1], 1, final_height, 1, 0),
# Rearrange("b c h w -> b (c h w)"),
# Sigmoid(),
# )
def forward(self, x: Tensor) -> Tensor:
x = self.hidden_layers(x)
x = self.classifier(x)
return x.squeeze() # remove dummy out_channels dimension
Exercise - Weight initialisation
```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵⚪⚪⚪
You should spend up to 10-15 minutes on this exercise. ```
The paper mentions at the end of page 3 that all weights were initialized from a $N(0, 0.02)$ distribution. This applies to the convolutional and convolutional transpose layers' weights (plus the weights in the linear classifier), but the BatchNorm layers' weights should be initialised from $N(1, 0.02)$ (since 1 is their default value). The BatchNorm biases should all be set to zero.
You can fill in the following function to initialise your weights, and call it within the __init__ method of your DCGAN. (Hint: you can use the functions nn.init.normal_ and nn.init.constant_ here.)
def initialize_weights(model: nn.Module) -> None:
"""
Initializes weights according to the DCGAN paper (details at the end of page 3 of the DCGAN
paper), by modifying the weights of the model in place.
"""
raise NotImplementedError()
tests.test_initialize_weights(initialize_weights, ConvTranspose2d, Conv2d, Linear, BatchNorm2d)
Solution
def initialize_weights(model: nn.Module) -> None:
"""
Initializes weights according to the DCGAN paper (details at the end of page 3 of the DCGAN
paper), by modifying the weights of the model in place.
"""
for module in model.modules():
if isinstance(module, (ConvTranspose2d, Conv2d, Linear)):
nn.init.normal_(module.weight.data, 0.0, 0.02)
elif isinstance(module, BatchNorm2d):
nn.init.normal_(module.weight.data, 1.0, 0.02)
nn.init.constant_(module.bias.data, 0.0)
Note - the tests for this aren't maximally strict, but don't worry if you don't get things exactly right, since your model will still probably train successfully. If you think you've got the architecture right but your model still isn't training, you might want to return here and check your initialisation.
model = DCGAN().to(device)
x = t.randn(3, 100).to(device)
print(torchinfo.summary(model.netG, input_data=x), end="\n\n")
print(torchinfo.summary(model.netD, input_data=model.netG(x)))
========================================================================================== Layer (type:depth-idx) Output Shape Param # ========================================================================================== Generator [3, 3, 64, 64] -- ├─Sequential: 1-1 [3, 512, 8, 8] -- │ └─Linear: 2-1 [3, 32768] 3,276,800 │ └─Rearrange: 2-2 [3, 512, 8, 8] -- │ └─BatchNorm2d: 2-3 [3, 512, 8, 8] 1,024 │ └─ReLU: 2-4 [3, 512, 8, 8] -- ├─Sequential: 1-2 [3, 3, 64, 64] -- │ └─Sequential: 2-5 [3, 256, 16, 16] -- │ │ └─ConvTranspose2d: 3-1 [3, 256, 16, 16] 2,097,152 │ │ └─BatchNorm2d: 3-2 [3, 256, 16, 16] 512 │ │ └─ReLU: 3-3 [3, 256, 16, 16] -- │ └─Sequential: 2-6 [3, 128, 32, 32] -- │ │ └─ConvTranspose2d: 3-4 [3, 128, 32, 32] 524,288 │ │ └─BatchNorm2d: 3-5 [3, 128, 32, 32] 256 │ │ └─ReLU: 3-6 [3, 128, 32, 32] -- │ └─Sequential: 2-7 [3, 3, 64, 64] -- │ │ └─ConvTranspose2d: 3-7 [3, 3, 64, 64] 6,144 │ │ └─Tanh: 3-8 [3, 3, 64, 64] -- ========================================================================================== Total params: 5,906,176 Trainable params: 5,906,176 Non-trainable params: 0 Total mult-adds (Units.GIGABYTES): 3.31 ========================================================================================== Input size (MB): 0.00 Forward/backward pass size (MB): 11.30 Params size (MB): 23.62 Estimated Total Size (MB): 34.93 ========================================================================================== ========================================================================================== Layer (type:depth-idx) Output Shape Param # ========================================================================================== Discriminator [3] -- ├─Sequential: 1-1 [3, 512, 8, 8] -- │ └─Sequential: 2-1 [3, 128, 32, 32] -- │ │ └─Conv2d: 3-1 [3, 128, 32, 32] 6,144 │ │ └─LeakyReLU: 3-2 [3, 128, 32, 32] -- │ └─Sequential: 2-2 [3, 256, 16, 16] -- │ │ └─Conv2d: 3-3 [3, 256, 16, 16] 524,288 │ │ └─BatchNorm2d: 3-4 [3, 256, 16, 16] 512 │ │ └─LeakyReLU: 3-5 [3, 256, 16, 16] -- │ └─Sequential: 2-3 [3, 512, 8, 8] -- │ │ └─Conv2d: 3-6 [3, 512, 8, 8] 2,097,152 │ │ └─BatchNorm2d: 3-7 [3, 512, 8, 8] 1,024 │ │ └─LeakyReLU: 3-8 [3, 512, 8, 8] -- ├─Sequential: 1-2 [3, 1] -- │ └─Rearrange: 2-4 [3, 32768] -- │ └─Linear: 2-5 [3, 1] 32,768 │ └─Sigmoid: 2-6 [3, 1] -- ========================================================================================== Total params: 2,661,888 Trainable params: 2,661,888 Non-trainable params: 0 Total mult-adds (Units.MEGABYTES): 824.28 ========================================================================================== Input size (MB): 0.15 Forward/backward pass size (MB): 7.86 Params size (MB): 10.65 Estimated Total Size (MB): 18.66 ==========================================================================================
Training loop
Recall, the goal of training the discriminator is to maximize the probability of correctly classifying a given input as real or fake. The goal of the generator is to produce images to fool the discriminator. This is framed as a minimax game, where the discriminator and generator try to solve the following:
The literature on minimax games is extensive, so we won't go into it here. It's better to understand this formula on an intuitive level:
- Given a fixed $G$ (generator), the goal of the discriminator is to produce high values for $D$ when fed real images $x$, and low values when fed fake images $G(z)$.
- The generator $G$ is searching for a strategy where, even if the discriminator $D$ was optimal, it would still find it hard to distinguish between real and fake images with high confidence.
Since we can't know the true distribution of $x$, we instead estimate the expression above by calculating it over a batch of real images $x$ (and some random noise $z$). This gives us a loss function to train against (since $D$ wants to maximise this value, and $G$ wants to minimise this value). For each batch, we perform gradient descent on the discriminator and then on the generator.
Training the discriminator
We take the following steps:
- Zero the gradients of $D$.
- This is important because if the last thing we did was evaluate $D(G(z))$ (in order to update the parameters of $G$), then $D$ will have stored gradients from that backward pass.
- Generate random noise $z$, and compute $D(G(z))$. Take the average of $\log(1 - D(G(z)))$, and we have the first part of our loss function.
- Note - you can use the same random noise (and even the same fake image) as in the generator step. But make sure you're using the detached version, because we don't want gradients to propagate back through the generator!
- Take the real images $x$ in the current batch, and use that to compute $\log(D(x))$. This gives us the second part of our loss function.
- We now add the two terms together, and perform gradient ascent (since we're trying to maximise this expression).
- You can perform gradient ascent by either flipping the sign of the thing you're doing a backward pass on, or passing the keyword argument
maximize=Truewhen defining your optimiser (all optimisers have this option).
- You can perform gradient ascent by either flipping the sign of the thing you're doing a backward pass on, or passing the keyword argument
Tip - when calculating $D(G(z))$, for the purpose of training the discriminator, it's best to first calculate $G(z)$ then call detach on this tensor before passing it to $D$. This is because you then don't need to worry about gradients accumulating for $G$.
Training the generator
We take the following steps:
- Zero the gradients of $G$.
- Generate random noise $z$, and compute $D(G(z))$.
- We don't use $\log(1 - D(G(z)))$ to calculate our loss function, instead we use $\log(D(G(z)))$ (and gradient ascent).
Question - can you explain why we use $\log(D(G(z))$? (The Google reading material mentions this but doesn't really explain it.)
Answer
Early in learning, when the generator is really bad at producing realistic images, it will be easy for the discriminator to distinguish between them. So $\log(1 - D(G(z)))$ will be very close to $\log(1) = 0$. The gradient of $\log$ at this point is quite flat, so there won't be a strong gradient with which to train $G$. To put it another way, a marginal improvement in $G$ will have very little effect on the loss function. On the other hand, $\log(D(G(z)))$ tends to negative infinity as $D(G(z))$ gets very small. So the gradients here are very steep, and a small improvement in $G$ goes a long way.
It's worth emphasising that these two functions are both monotonic in opposite directions, so maximising one is equivalent to minimising the other. We haven't changed anything fundamental about how the GAN works; this is just a trick to help with gradient descent.
Note - PyTorch's BCELoss clamps its log function outputs to be greater than or equal to -100. This is because in principle our loss function could be negative infinity (if we take log of zero). You might find you need to employ a similar trick if you're manually computing the log of probabilities. Aside from the clamping, the following two code snippets are equivalent:
# Calculating loss manually, without clamping:
loss = - t.log(D_G_z)
# Calculating loss with clamping behaviour:
labels_real = t.ones_like(D_G_z)
loss = nn.BCELoss()(D_G_z, labels_real)
Optimizers
The generator and discriminator will have separate optimizers (this makes sense, since we'll have separate training steps for these two, and both are "trying" to optimize different things). The paper describes using an Adam optimizer with learning rate 0.0002, and momentum parameters $\beta_1 = 0.5, \beta_2 = 0.999$. This is set up for you already, in the __init__ block below.
Gradient Clipping
Gradient clipping is a useful technique for improving the stability of certain training loops, especially those like DCGANs which have potentially unstable loss functions. The idea is that you clip the gradients of your weights to some fixed threshold during backprop, and use these clipped gradients to update the weights. This can be done using nn.utils.clip_grad_norm, which is called between the loss.backward() and optimizer.step() methods (since it directly modifies the .grad attributes of your weights). You shouldn't find this absolutely necessary to train your models, however it might help to clip the gradients to a value like 1.0 for your generator & discriminator. We've given you this as an optional parameter to use in your DCGANArgs dataclass.
Exercise - implement GAN training loop
```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵🔵🔵⚪
You should spend up to 30-45 minutes on this exercise. ```
You should now implement your training loop below. We've filled in the __init__ method for you, as well as log_samples method which determines the core structure of the training loop. Your task is to:
- Fill in the two functions
training_step_discriminatorandtraining_step_generator, which perform a single gradient step on the discriminator and generator respectively.- Note that the discriminator training function takes two arguments: the real and fake image (in the notation above, $x$ and $z$), because it trains to distinguish real and fake. The generator training function only takes the fake image $z$, because it trains to fool the discriminator.
- Also note, you should increment
self.steponly once per (discriminator & generator) step, not for both.
- Fill in the
trainmethod, which should perform the training loop over the number of epochs specified inargs.epochs. This will be similar to previous training loops, but with a few key differences we'll highlight here:- You'll need to compute both losses from
training_step_generatorandtraining_step_discriminator. For the former you should pass in just the fake image (you're only training the generator to produce better fake images), for the latter you should pass in the real image and the detached fake image i.e.img.detach()(because you're training the discriminator to tell real from fake, and you don't want gradients propagating back to the generator).- The fake image should be created from random noise
t.randn(batch_size, latent_dim_size)and passing it into your generator.
- The fake image should be created from random noise
- Once again the trainloader gives us an iterable of
(img, label)but we don't need to use the labels (because all these images are real, and that's all we care about).
- You'll need to compute both losses from
Again, we recommend not using wandb until you've got your non-wandb based code working without errors. Once the generator loss is going down (or at least not exploding!) then you can enable it. However, an important note - generator loss going down is does not imply the model is working, and vice-versa! For training systems as unstable as GANs, the best you can do is often just inspecting the output. Although it varies depending on details of the hardware and dataset & model you're training with, at least for these exercises if your generator's output doesn't resemble anything like a face after the first epoch, then something's probably going wrong in your code.
@dataclass
class DCGANArgs:
"""
Class for the arguments to the DCGAN (training and architecture).
Note, we use field(defaultfactory(...)) when our default value is a mutable object.
"""
# architecture
latent_dim_size: int = 100
hidden_channels: list[int] = field(default_factory=lambda: [128, 256, 512])
# data & training
dataset: Literal["MNIST", "CELEB"] = "CELEB"
batch_size: int = 64
epochs: int = 3
lr: float = 0.0002
betas: tuple[float, float] = (0.5, 0.999)
clip_grad_norm: float | None = 1.0
# logging
use_wandb: bool = False
wandb_project: str | None = "day5-gan"
wandb_name: str | None = None
log_every_n_steps: int = 250
class DCGANTrainer:
def __init__(self, args: DCGANArgs):
self.args = args
self.trainset = get_dataset(self.args.dataset)
self.trainloader = DataLoader(
self.trainset, batch_size=args.batch_size, shuffle=True, num_workers=8
)
batch, img_channels, img_height, img_width = next(iter(self.trainloader))[0].shape
assert img_height == img_width
self.model = (
DCGAN(args.latent_dim_size, img_height, img_channels, args.hidden_channels)
.to(device)
.train()
)
self.optG = t.optim.Adam(self.model.netG.parameters(), lr=args.lr, betas=args.betas)
self.optD = t.optim.Adam(self.model.netD.parameters(), lr=args.lr, betas=args.betas)
def training_step_discriminator(
self,
img_real: Float[Tensor, "batch channels height width"],
img_fake: Float[Tensor, "batch channels height width"],
) -> Float[Tensor, ""]:
"""
Generates a real and fake image, and performs a gradient step on the discriminator to
maximize log(D(x)) + log(1-D(G(z))). Logs to wandb if enabled.
"""
raise NotImplementedError()
def training_step_generator(
self, img_fake: Float[Tensor, "batch channels height width"]
) -> Float[Tensor, ""]:
"""
Performs a gradient step on the generator to maximize log(D(G(z))). Logs to wandb if enabled.
"""
raise NotImplementedError()
@t.inference_mode()
def log_samples(self) -> None:
"""
Performs evaluation by generating 8 instances of random noise and passing them through the
generator, then optionally logging the results to Weights & Biases.
"""
assert self.step > 0, (
"First call should come after a training step. Remember to increment `self.step`."
)
self.model.netG.eval()
# Generate random noise
t.manual_seed(42)
noise = t.randn(10, self.model.latent_dim_size).to(device)
# Get generator output
output = self.model.netG(noise)
# Clip values to make the visualization clearer
output = output.clamp(output.quantile(0.01), output.quantile(0.99))
# Log to weights and biases
if self.args.use_wandb:
output = einops.rearrange(output, "b c h w -> b h w c").cpu().numpy()
wandb.log({"images": [wandb.Image(arr) for arr in output]}, step=self.step)
else:
display_data(output, nrows=1, title="Generator-produced images")
self.model.netG.train()
def train(self) -> DCGAN:
"""Performs a full training run."""
self.step = 0
if self.args.use_wandb:
wandb.init(project=self.args.wandb_project, name=self.args.wandb_name)
for epoch in range(self.args.epochs):
progress_bar = tqdm(self.trainloader, total=len(self.trainloader), ascii=True)
for img_real, label in progress_bar:
# YOUR CODE HERE - fill in the training step for generator & discriminator
if self.args.use_wandb:
wandb.finish()
return self.model
Help - I'm getting OOMs/crashes when I try to use the trainloader
This is a known issue on MacOS machines. To fix this, try adding multiprocessing_context="fork" to your DataLoader instantiation.
Solution
def training_step_discriminator(
self,
img_real: Float[Tensor, "batch channels height width"],
img_fake: Float[Tensor, "batch channels height width"],
) -> Float[Tensor, ""]:
"""
Generates a real and fake image, and performs a gradient step on the discriminator to maximize
log(D(x)) + log(1-D(G(z))). Logs to wandb if enabled.
"""
# Zero gradients
self.optD.zero_grad()
# Calculate D(x) and D(G(z)), for use in the objective function
D_x = self.model.netD(img_real)
D_G_z = self.model.netD(img_fake)
# Calculate loss
lossD = -(t.log(D_x).mean() + t.log(1 - D_G_z).mean())
# Gradient descent step (with optional clipping)
lossD.backward()
if self.args.clip_grad_norm is not None:
nn.utils.clip_grad_norm_(self.model.netD.parameters(), self.args.clip_grad_norm)
self.optD.step()
if self.args.use_wandb:
wandb.log(dict(lossD=lossD), step=self.step)
return lossD
def training_step_generator(self, img_fake: Float[Tensor, "batch channels height width"]) -> Float[Tensor, ""]:
"""
Performs a gradient step on the generator to maximize log(D(G(z))). Logs to wandb if enabled.
"""
# Zero gradients
self.optG.zero_grad()
# Calculate D(G(z)), for use in the objective function
D_G_z = self.model.netD(img_fake)
# Calculate loss
lossG = -(t.log(D_G_z).mean())
# Gradient descent step (with optional clipping)
lossG.backward()
if self.args.clip_grad_norm is not None:
nn.utils.clip_grad_norm_(self.model.netG.parameters(), self.args.clip_grad_norm)
self.optG.step()
if self.args.use_wandb:
wandb.log(dict(lossG=lossG), step=self.step)
return lossG
def train(self) -> DCGAN:
"""Performs a full training run."""
self.step = 0
if self.args.use_wandb:
wandb.init(project=self.args.wandb_project, name=self.args.wandb_name)
for epoch in range(self.args.epochs):
progress_bar = tqdm(self.trainloader, total=len(self.trainloader), ascii=True)
for img_real, label in progress_bar:
# Generate random noise & fake image
noise = t.randn(self.args.batch_size, self.args.latent_dim_size).to(device)
img_real = img_real.to(device)
img_fake = self.model.netG(noise)
# Training steps
lossD = self.training_step_discriminator(img_real, img_fake.detach())
lossG = self.training_step_generator(img_fake)
# Update progress bar
self.step += 1
progress_bar.set_description(f"{epoch=}, {lossD=:.4f}, {lossG=:.4f}, batches={self.step}")
# Log batch of data
if self.step % self.args.log_every_n_steps == 0:
self.log_samples()
if self.args.use_wandb:
wandb.finish()
return self.model
Once you've written your code, here are some default arguments for MNIST and CelebA you can try out.
Note that the MNIST model is very small in comparison to CelebA - if you make it any larger, you fall into a very common GAN failure mode where the discriminator becomes perfect (loss goes to zero) and the generator is unable to get a gradient signal to produce better images - see next section for a discussion of this. Larger architectures are generally more likely to fall into this failure mode, and empirically it seems to happen more for MNIST than for CelebA which is why we generally recommend using the CelebA dataset & architecture for this exercise - although this failure mode can happen in both cases!
# Arguments for CelebA
args = DCGANArgs(
dataset="CELEB",
hidden_channels=[128, 256, 512],
batch_size=32, # if you get OOM errors, reduce this!
epochs=5,
use_wandb=False,
)
trainer = DCGANTrainer(args)
dcgan = trainer.train()
Click to see an example of the output you should be producing by the end of this CelebA training run.
Here was my output after 250 batches (8000 images):

After 2000 batches (64000 images):

And after the end of training (5 epochs, approx 625k images):

# Arguments for MNIST
args = DCGANArgs(
dataset="MNIST",
hidden_channels=[12, 24],
epochs=20,
batch_size=128,
use_wandb=False,
)
trainer = DCGANTrainer(args)
dcgan = trainer.train()
Click to see an example of the output you should be producing by the end of this MNIST training run.
Here was my output after 250 batches (32k images):

After 2000 batches (256k images):

About 90% of the way through training, it was achieving the best results:

However after this point it broke, and produced NaNs from both the discriminator and the generator:

This is a common problem for training GANs - they're just a pretty cursed architecture! Read on for more on this.
Fixing bugs
GANs are notoriously hard to get exactly right. I ran into quite a few bugs myself building this architecture, and I've tried to mention them somewhere on this page to help participants avoid them. If you run into a bug and are able to fix it, please send it to me and I can add it here, for the benefit of everyone else!
- Make sure you apply the layer normalization (mean 0, std dev 0.02) to your linear layers as well as your convolutional layers.
- More generally, in your function to initialise the weights of your network, make sure no layers are being missed out. The easiest way to do this is to inspect your model afterwards (i.e. loop through all the params, printing out their mean and std dev).
Also, you might find this page useful. It provides several tips and tricks for how to make your GAN work (many of which we've already mentioned on this page).
Why so unstable during training?
If you try training your GAN on MNIST, you might find that it eventually blows up (with close to zero discriminator loss, and spiking generator loss - possibly even gradients large enough to overflow and lead to nan values). This might also happen if you train on CelebA but your architecture is too big, or even if you train with a reasonably-sized architecture but for too long!
This is a common problem with GANs, which are notoriously unstable to train. Essentially, the discriminator gets so good at its job that the generator can't latch onto a good gradient for improving its performance. Although the theoretical formulation of GANs as a minimax game is elegant, there are quite a few assumptions that have to go into it in order for there to be one theoretical optimum involving the generator producing perfect images - and in practice this is rarely achieved, even in the limit.
Different architectures like diffusion models and VAEs are generally more stable, although many of the most advanced image generation architectures do still take important conceptual ideas from the GAN framework.
Bonus - Smooth interpolation
Suppose you take two vectors in the latent space. If you use your generator to create output at points along the linear interpolation between these vectors, your image will change continuously (because it is a continuous function of the latent vector), but it might look very different at the start and the end. Can you create any cool animations from this?
Instead of linearly interpolating between two vectors, you could try applying a rotation matrix to a vector (this has the advantage of keeping the interpolated vector "in distribution", since the rotation between two standard normally distributed vectors is also standard normal, whereas the linear interpolation isn't). Are the results better?