2️⃣ Autograd

Learning Objectives

Perform a topological sort of a computational graph (and understand why this is important).

Implement a the backprop function, to calculate and store gradients for all tensors in a computational graph.

Now, rather than figuring out which backward functions to call, in what order, and what their inputs should be, we'll write code that takes care of that for us. We'll implement this with a few major components:

Tensor, which is a wrapper around numpy arrays which is equivalent to PyTorch's Tensor class
Recipe, which tracks the extra information needed to run backpropagation (mainly how this tensor was created from other tensors)
wrap_forward_fn, which takes a numpy function mapping arrays to arrays (e.g. np.log) and returns a new function that maps tensors to tensors (while also creating the recipe for the new tensor)

Wrapping Arrays (Tensor)

We're going to wrap each array with a wrapper object from our library which we'll call Tensor because it's going to behave similarly to a torch.Tensor.

Each Tensor that is created by one of our forward functions will have a Recipe, which tracks the extra information need to run backpropagation.

wrap_forward_fn will take a forward function and return a new forward function that does the same thing while recording the info we need to do backprop in the Recipe.

Recipe

Let's start by taking a look at Recipe.

@dataclass is a handy class decorator that sets up an __init__ function for the class that takes the provided attributes as arguments and sets them as you'd expect.

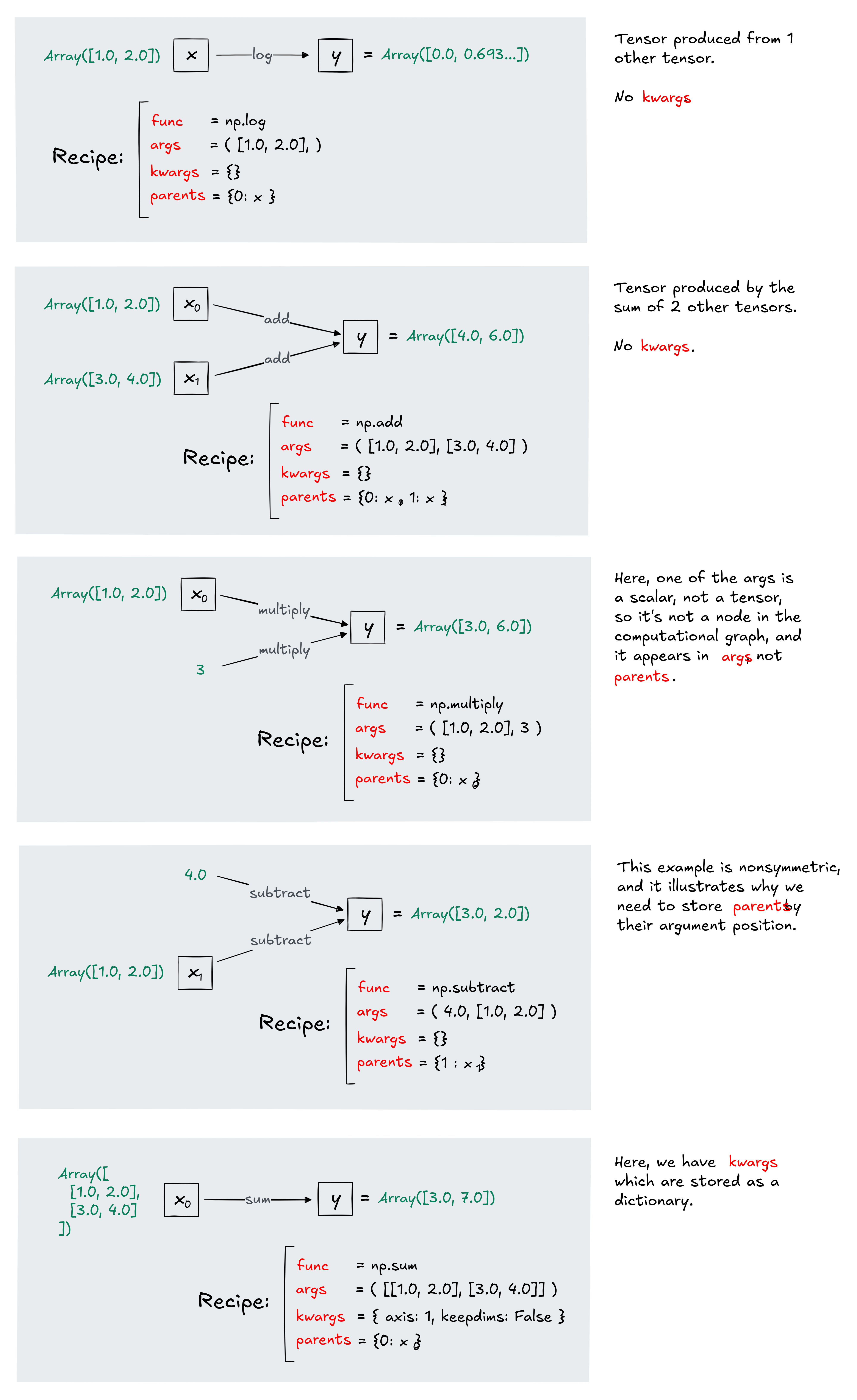
The class Recipe is designed to track the forward functions in our computational graph, so that gradients can be calculated during backprop. Each tensor created by a forward function has its own Recipe. We're naming it this because it is a set of instructions that tell us which ingredients went into making our tensor: what the function was, and what tensors were used as input to the function to produce this one as output.

@dataclass(frozen=True)
class Recipe:
    """Extra information necessary to run backpropagation. You don't need to modify this."""

    func: Callable
    "The 'inner' NumPy function that does the actual forward computation."
    "Note, we call it 'inner' to distinguish it from the wrapper we'll create for it later on."

    args: tuple
    "The input arguments passed to func."
    "For instance, if func=np.sum then args would be a length-1 tuple with the tensor to be summed."

    kwargs: dict[str, Any]
    "Keyword arguments passed to func."
    "For instance, if func was np.sum then kwargs might contain 'dim' and 'keepdims'."

    parents: dict[int, "Tensor"]
    "Map from positional argument index to the Tensor at that position."
    "For passing gradients back along the computational graph."

Note that args just stores the values of the underlying arrays, but parents stores the actual tensors. This is because they serve two different purposes: args is required for computing the value of gradients during backpropagation, and parents is required to infer the structure of the computational graph (i.e. which tensors were used to produce which other tensors).

Here are some examples, to build intuition for what the four fields of Recipe are, and why we need all four of them to fully describe a tensor in our graph and how it was created. Make sure you understand each of these examples before moving on, because it'll really help you progress quickly through the following exercises.

Registering backwards functions

The Recipe takes care of tracking the forward functions in our computational graph, but we still need a way to find the backward function corresponding to a given forward function when we do backprop (or possibly the set of backward functions, if the forward function takes more than one argument).

Exercise - implement `BackwardFuncLookup`

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 10-15 minutes on these exercises. These exercises should be very short, once you understand what is being asked. ```

We will define a class BackwardFuncLookup in order to find the backward function for a given forward function. The implementation details are left up to you - all that matters is that you pass the test code in the cell below. Reading this test code should explain how the BackwardFuncLookup class needs to be used - for any given forward function e.g. np.log, we need to be able to add a set of backward functions for each of its positional arguments.

class BackwardFuncLookup:
    def __init__(self) -> None:
        raise NotImplementedError()

    def add_back_func(self, forward_fn: Callable, arg_position: int, back_fn: Callable) -> None:
        raise NotImplementedError()

    def get_back_func(self, forward_fn: Callable, arg_position: int) -> Callable:
        raise NotImplementedError()


BACK_FUNCS = BackwardFuncLookup()

BACK_FUNCS.add_back_func(np.log, 0, log_back)
BACK_FUNCS.add_back_func(np.multiply, 0, multiply_back0)
BACK_FUNCS.add_back_func(np.multiply, 1, multiply_back1)

assert BACK_FUNCS.get_back_func(np.log, 0) == log_back
assert BACK_FUNCS.get_back_func(np.multiply, 0) == multiply_back0
assert BACK_FUNCS.get_back_func(np.multiply, 1) == multiply_back1

print("Tests passed - BackwardFuncLookup class is working as expected!")

Help - I'm stuck on this implementation

You can define a dict like self.back_funcs in the __init__ method. When you add / retrieve a function, you can use the tuple (forward_fn, arg_position) as a key, and the backward function as the value.

Solution

class BackwardFuncLookup:
    def __init__(self) -> None:
        self.back_funcs = {}  # each entry is a tuple of (forward_fn, arg_position) -> back_fn
def add_back_func(self, forward_fn: Callable, arg_position: int, back_fn: Callable) -> None:
        self.back_funcs[(forward_fn, arg_position)] = back_fn
def get_back_func(self, forward_fn: Callable, arg_position: int) -> Callable:
        return self.back_funcs[(forward_fn, arg_position)]

Tensors

Our Tensor object has these fields:

An array field of type np.ndarray. These are the actual tensor values.
A requires_grad field of type bool. This determines whether we need to compute gradients for this tensor (note this doesn't necessarily mean we need to store them, see below).
A grad field of the same size and type as the value. This is where gradients are stored.
A recipe field, as we've already seen. A tensor has a recipe if and only if it was created by some operation on other tensors.

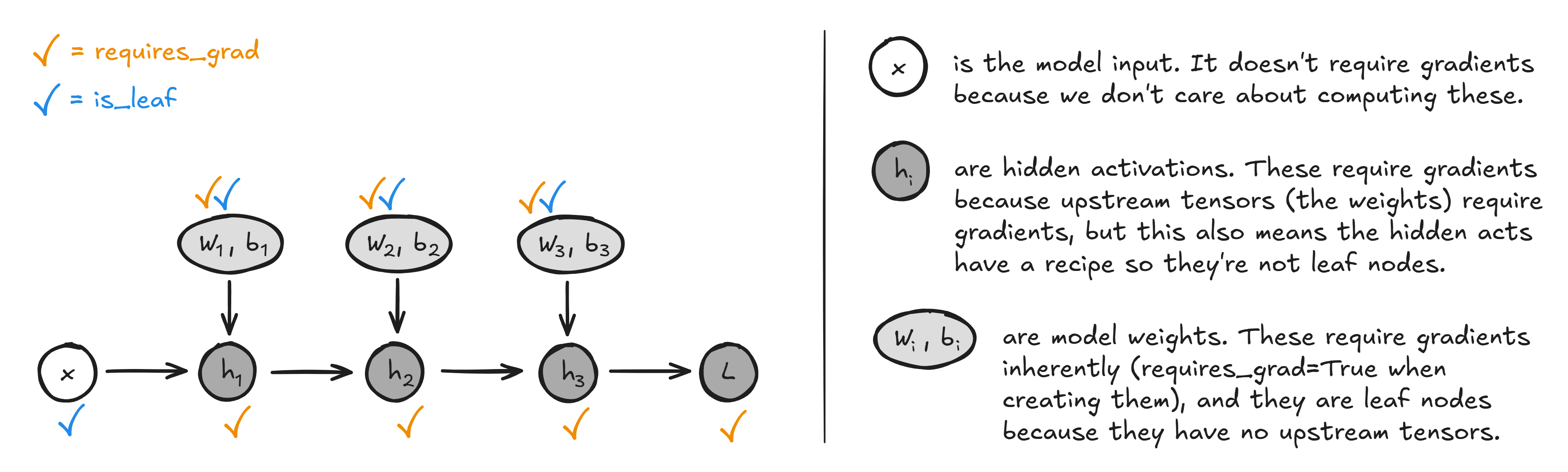
`requires_grad` and `is_leaf`

The meaning of requires_grad is that when doing operations using this tensor, the recipe will be stored and it and any descendents will be included in the computational graph. Note that requires_grad does not necessarily mean that we will save the accumulated gradients to this tensor's .grad parameter when doing backprop - for example we require gradients to propagate through the hidden activations of a neural network to get back to grads for our model weights, but we don't need to actually store the gradients of the hidden activations.

We use is_leaf to differentiate between these cases (see the method Tensor.is_leaf defined below) - a leaf tensor is one that represents the end of a backprop path, either because it doesn't require gradients or it has no nodes further back in the computational graph which require gradients. So our backprop algorithm will always terminate at a leaf node, then store that leaf node's gradient as .grad only if requires_grad is true.

You can investigate this by running the following code:

layer = torch.nn.Linear(3, 4)
input = torch.ones(3)
output = layer(input)

print(layer.weight.is_leaf)       # -> True
print(layer.weight.requires_grad) # -> True

print(output.is_leaf)             # -> False
print(output.requires_grad)       # -> True

print(input.is_leaf)              # -> True
print(input.requires_grad)        # -> False

When creating tensors, we can set requires_grad explicitly (e.g. it's false by default for most tensors, but is true by default if that tensor is wrapped in torch.nn.Parameter - we'll create our own version of this later). When creating a tensor from another tensor or tensors, requires_grad is true if and only if all of the following 3 conditions hold:

Global grad tracking is enabled. In this notebook we've represented this with the global variable grad_tracking_enabled, but in PyTorch this is done with torch.set_grad_enabled(False). This is useful because when you're looking at a model in inference mode, gradient tracking can waste memory and it's useful to disable it (we'll do this a lot next week, when we study transformer interpretability).
At least one of the input tensors requires grad (since this is equivalent to "there are other tensors further upstream which we need to get gradients for").
The function is differentiable (if not, obviously we can't compute gradients).

Now, we're giving you the full Tensor class. Most of these methods are currently undefined, and you'll go on to define them in later exercises (so you won't need to write any code this class). For now, just pay attention to the docstring & __init__ methods.

Arr = np.ndarray


class Tensor:
    """
    A drop-in replacement for torch.Tensor supporting a subset of features.
    """

    array: Arr
    "The underlying array. Can be shared between multiple Tensors."
    requires_grad: bool
    "If True, calling functions or methods on this tensor will track relevant data for backprop."
    grad: "Tensor | None"
    "Backpropagation will accumulate gradients into this field."
    recipe: "Recipe | None"
    "Extra information necessary to run backpropagation."

    def __init__(self, array: Arr | list, requires_grad=False):
        self.array = array if isinstance(array, Arr) else np.array(array)
        if self.array.dtype == np.float64:
            self.array = self.array.astype(np.float32)
        self.requires_grad = requires_grad
        self.grad = None
        self.recipe = None
        "If not None, this tensor's array was created as recipe.func(*recipe.args, **recipe.kwargs)."

    def __neg__(self) -> "Tensor":
        return negative(self)

    def __add__(self, other) -> "Tensor":
        return add(self, other)

    def __radd__(self, other) -> "Tensor":
        return add(other, self)

    def __sub__(self, other) -> "Tensor":
        return subtract(self, other)

    def __rsub__(self, other) -> "Tensor":
        return subtract(other, self)

    def __mul__(self, other) -> "Tensor":
        return multiply(self, other)

    def __rmul__(self, other):
        return multiply(other, self)

    def __truediv__(self, other):
        return true_divide(self, other)

    def __rtruediv__(self, other):
        return true_divide(other, self)

    def __matmul__(self, other):
        return matmul(self, other)

    def __rmatmul__(self, other):
        return matmul(other, self)

    def __eq__(self, other):
        return eq(self, other)

    def __repr__(self) -> str:
        return f"Tensor({repr(self.array)}, requires_grad={self.requires_grad})"

    def __len__(self) -> int:
        if self.array.ndim == 0:
            raise TypeError
        return self.array.shape[0]

    def __hash__(self) -> int:
        return id(self)

    def __getitem__(self, index) -> "Tensor":
        return getitem(self, index)

    def add_(self, other: "Tensor", alpha: float = 1.0) -> "Tensor":
        add_(self, other, alpha=alpha)
        return self

    def sub_(self, other: "Tensor", alpha: float = 1.0) -> "Tensor":
        sub_(self, other, alpha=alpha)
        return self

    def __iadd__(self, other: "Tensor") -> "Tensor":
        self.add_(other)
        return self

    def __isub__(self, other: "Tensor") -> "Tensor":
        self.sub_(other)
        return self

    @property
    def T(self) -> "Tensor":
        return permute(self, axes=(-1, -2))

    def item(self):
        return self.array.item()

    def sum(self, dim=None, keepdim=False) -> "Tensor":
        return sum(self, dim=dim, keepdim=keepdim)

    def log(self) -> "Tensor":
        return log(self)

    def exp(self) -> "Tensor":
        return exp(self)

    def reshape(self, new_shape) -> "Tensor":
        return reshape(self, new_shape)

    def permute(self, dims) -> "Tensor":
        return permute(self, dims)

    def maximum(self, other) -> "Tensor":
        return maximum(self, other)

    def relu(self) -> "Tensor":
        return relu(self)

    def argmax(self, dim=None, keepdim=False) -> "Tensor":
        return argmax(self, dim=dim, keepdim=keepdim)

    def uniform_(self, low: float, high: float) -> "Tensor":
        self.array[:] = np.random.uniform(low, high, self.array.shape)
        return self

    def backward(self, end_grad: "Arr | Tensor | None" = None) -> None:
        if isinstance(end_grad, Arr):
            end_grad = Tensor(end_grad)
        return backprop(self, end_grad)

    def size(self, dim: int | None = None):
        if dim is None:
            return self.shape
        return self.shape[dim]

    @property
    def shape(self):
        return self.array.shape

    @property
    def ndim(self):
        return self.array.ndim

    @property
    def is_leaf(self):
        """Same as https://pytorch.org/docs/stable/generated/torch.Tensor.is_leaf.html"""
        if self.requires_grad and self.recipe and self.recipe.parents:
            return False
        return True

    def __bool__(self):
        if np.array(self.shape).prod() != 1:
            raise RuntimeError("bool value of Tensor with more than one value is ambiguous")
        return bool(self.item())


def empty(*shape: int) -> Tensor:
    """Like torch.empty."""
    return Tensor(np.empty(shape))


def zeros(*shape: int) -> Tensor:
    """Like torch.zeros."""
    return Tensor(np.zeros(shape))


def arange(start: int, end: int, step=1) -> Tensor:
    """Like torch.arange(start, end)."""
    return Tensor(np.arange(start, end, step=step))


def tensor(array: Arr, requires_grad=False) -> Tensor:
    """Like torch.tensor."""
    return Tensor(array, requires_grad=requires_grad)

Forward Pass: Building the Computational Graph

Let's start with a simple case: our log function. log_forward is a wrapper, which should implement the functionality of np.log but work with tensors rather than arrays.

Exercise - implement `log_forward`

```yaml Difficulty: 🔴🔴🔴⚪⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 15-20 minutes on this exercise. ```

Your log function should be a wrapper around np.log, which takes and returns a Tensor object rather than numpy arrays. You can refer to the first of the five diagrams at the start of the "Recipe" section if you're stuck.

Some more hints / tips:

As a reminder, requires_grad is true if both global gradient tracking is enabled (i.e. grad_tracking_enabled is true) and at least one of the inputs has requires_grad true.
You should also set the recipe for the new tensor, if requires_grad is true (if not then you can just set the recipe to None).

Later we'll write code to wrap numpy functions in a generic and reusable way, but for now we just want to get this working for np.log.

def log_forward(x: Tensor) -> Tensor:
    """Performs np.log on a Tensor object."""
    raise NotImplementedError()


log = log_forward
tests.test_log(Tensor, log_forward)
tests.test_log_no_grad(Tensor, log_forward)
a = Tensor([1], requires_grad=True)
grad_tracking_enabled = False
b = log_forward(a)
grad_tracking_enabled = True
assert not b.requires_grad, "should not require grad if grad tracking globally disabled"
assert b.recipe is None, "should not create recipe if grad tracking globally disabled"

Solution

def log_forward(x: Tensor) -> Tensor:
    """Performs np.log on a Tensor object."""
    # Get the function output (as a numpy array)
    array = np.log(x.array)
# Find whether the tensor requires grad
    requires_grad = grad_tracking_enabled and x.requires_grad
# Create the tensor
    out = Tensor(array, requires_grad)
# Set the recipe (if we need it)
    if requires_grad:
        out.recipe = Recipe(func=np.log, args=(x.array,), kwargs={}, parents={0: x})
return out

Now let's do the same for multiply, to see how to handle functions with multiple arguments.

Exercise - implement `multiply_forward`

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 15-20 minutes on this exercise. ```

There are a few differences between this and log:

The actual function to be called is different
We need more than one argument in args and parents, when defining Recipe
requires_grad should be true if grad_tracking_enabled=True, and ANY of the input tensors require grad
One of the inputs may be an int, so you'll need to deal with this case before calculating out

If you're confused, you can scroll up to the diagram at the top of the page (which tells you how to construct the recipe for functions like multiply or add when they are both arrays, or when one is an array and the other is a scalar).

def multiply_forward(a: Tensor | int, b: Tensor | int) -> Tensor:
    """Performs np.multiply on a Tensor object."""
    assert isinstance(a, Tensor) or isinstance(b, Tensor)

    # Get all function arguments as non-tensors (i.e. either ints or arrays)
    arg_a = a.array if isinstance(a, Tensor) else a
    arg_b = b.array if isinstance(b, Tensor) else b

    raise NotImplementedError()


multiply = multiply_forward
tests.test_multiply(Tensor, multiply_forward)
tests.test_multiply_no_grad(Tensor, multiply_forward)
tests.test_multiply_float(Tensor, multiply_forward)
a = Tensor([2], requires_grad=True)
b = Tensor([3], requires_grad=True)
grad_tracking_enabled = False
b = multiply_forward(a, b)
grad_tracking_enabled = True
assert not b.requires_grad, "should not require grad if grad tracking globally disabled"
assert b.recipe is None, "should not create recipe if grad tracking globally disabled"

Help - I get AttributeError: 'int' object has no attribute 'array'.

Remember that your multiply function should also accept integers. You need to separately deal with the cases where a and b are integers or Tensors.

Help - I get AssertionError: assert len(c.recipe.parents) == 1 and c.recipe.parents[0] is a in the "test_multiply_float" test.

This is probably because you've stored the inputs to multiply as integers when one of the is an integer. Remember, parents should just be a list of the Tensors that were inputs to multiply, so you shouldn't add ints.

Solution

def multiply_forward(a: Tensor | int, b: Tensor | int) -> Tensor:
    """Performs np.multiply on a Tensor object."""
    assert isinstance(a, Tensor) or isinstance(b, Tensor)
# Get all function arguments as non-tensors (i.e. either ints or arrays)
    arg_a = a.array if isinstance(a, Tensor) else a
    arg_b = b.array if isinstance(b, Tensor) else b
# Calculate the output (which is a numpy array)
    out_arr = arg_a * arg_b
    assert isinstance(out_arr, np.ndarray)
# Find whether the tensor requires grad (need to check if ANY of the inputs do)
    requires_grad = grad_tracking_enabled and any(
        [isinstance(x, Tensor) and x.requires_grad for x in (a, b)]
    )
# Create the output tensor from the underlying data and the requires_grad flag
    out = Tensor(out_arr, requires_grad)
# If requires_grad, then create a recipe
    if requires_grad:
        parents = {idx: arr for idx, arr in enumerate([a, b]) if isinstance(arr, Tensor)}
        out.recipe = Recipe(np.multiply, (arg_a, arg_b), {}, parents)
return out

Forward Pass - Generic Version

All our forward functions are going to look extremely similar to log_forward and multiply_forward. Implement the higher order function wrap_forward_fn that takes a Arr -> Arr function and returns a Tensor -> Tensor function. In other words, wrap_forward_fn(np.multiply) should evaluate to a callable that does the same thing as your multiply_forward (and same for np.log).

Exercise - implement `wrap_forward_fn`

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵🔵🔵🔵⚪

You should spend up to 20-25 minutes on this exercise. This exercise is probably the 2nd most conceptually important today, after the backprop implementation at the end of the section. ```

If you're stuck, you can start with the same structure as the wrapped multiply function above (i.e. just copy and paste the code from solutions and use this as a stand in for tensor_func below, then modify it).

def wrap_forward_fn(numpy_func: Callable, is_differentiable=True) -> Callable:
    """
    Args:
        numpy_func:
            takes any number of positional arguments, some of which may be NumPy arrays, and any
            number of keyword arguments which we aren't allowing to be NumPy arrays at present. It
            returns a single NumPy array.

        is_differentiable:
            if True, numpy_func is differentiable with respect to some input argument, so we may
            need to track information in a Recipe. If False, we definitely don't need to track
            information.

    Returns:
        tensor_func
            It has the same signature as numpy_func, except it operates on Tensors instead of Arr.
    """

    def tensor_func(*args: Any, **kwargs: Any) -> Tensor:
        # Get all function arguments as non-tensors (i.e. either ints or arrays)
        arg_arrays = tuple([(a.array if isinstance(a, Tensor) else a) for a in args])

        # YOUR CODE HERE - create output array & make it a tensor with requires_grad (& recipe)

        return out

    return tensor_func


def _sum(x: Arr, dim=None, keepdim=False) -> Arr:
    # need to be careful with sum, because kwargs have different names in torch and numpy
    return np.sum(x, axis=dim, keepdims=keepdim)


log = wrap_forward_fn(np.log)
multiply = wrap_forward_fn(np.multiply)
eq = wrap_forward_fn(np.equal, is_differentiable=False)
sum = wrap_forward_fn(_sum)

tests.test_log(Tensor, log)
tests.test_log_no_grad(Tensor, log)
tests.test_multiply(Tensor, multiply)
tests.test_multiply_no_grad(Tensor, multiply)
tests.test_multiply_float(Tensor, multiply)
tests.test_eq(Tensor, eq)
tests.test_sum(Tensor)

Help - I'm getting NameError: name 'getitem' is not defined.

This is probably because you're calling numpy_func on the args themselves. Recall that args will be a list of Tensor objects, and that you should call numpy_func on the underlying arrays.

Help - I'm getting an AssertionError on assert c.requires_grad == True (or something similar).

This is probably because you're not defining requires_grad correctly. Remember that the output of a forward function should have requires_grad = True if and only if all of the following hold:

Grad tracking is enabled The function is differentiable * Any of the inputs are tensors with requires_grad = True

Help - my function passes all tests up to test_sum, but then fails here.

test_sum, unlike the previous tests, wraps a function that uses keyword arguments. So if you're failing here, it's probably because you didn't use kwargs correctly. kwargs should be used in two ways: once when actually calling the numpy_func, and once when defining the Recipe object for the output tensor.

Solution

def wrap_forward_fn(numpy_func: Callable, is_differentiable=True) -> Callable:
    """
    Args:
        numpy_func:
            takes any number of positional arguments, some of which may be NumPy arrays, and any
            number of keyword arguments which we aren't allowing to be NumPy arrays at present. It
            returns a single NumPy array.
        is_differentiable:
            if True, numpy_func is differentiable with respect to some input argument, so we may
            need to track information in a Recipe. If False, we definitely don't need to track
            information.
    Returns:
        tensor_func
            It has the same signature as numpy_func, except it operates on Tensors instead of Arr.
    """
def tensor_func(*args: Any, **kwargs: Any) -> Tensor:
        # Get all function arguments as non-tensors (i.e. either ints or arrays)
        arg_arrays = tuple([(a.array if isinstance(a, Tensor) else a) for a in args])
# Calculate the output (which is a numpy array)
        out_arr = numpy_func(*arg_arrays, **kwargs)
# Find whether the tensor requires grad (need to check if ANY of the inputs do)
        requires_grad = (
            grad_tracking_enabled
            and is_differentiable
            and any([(isinstance(a, Tensor) and a.requires_grad) for a in args])
        )
# Create the output tensor from the underlying data and the requires_grad flag
        out = Tensor(out_arr, requires_grad)
# If requires_grad, then create a recipe
        if requires_grad:
            parents = {idx: a for idx, a in enumerate(args) if isinstance(a, Tensor)}
            out.recipe = Recipe(numpy_func, arg_arrays, kwargs, parents)
return out
return tensor_func

Note - none of these functions involve keyword args, so the tests won't detect if you're handling kwargs incorrectly (or even failing to use them at all). If your code fails in later exercises, you might want to come back here and check that you're using the kwargs correctly. Alternatively, once you pass the tests, you can compare your code to the solutions and see how they handle kwargs.

Backpropagation

Now all the pieces are in place to implement backpropagation. We need to loop over our nodes from right to left (i.e. starting with the tensors computed last and moving backwards chronologically). At each node, we:

Call the backward function to transform the grad wrt output to the grad wrt input.
If the node is a leaf, write the grad to the grad field.
Otherwise, accumulate the grad into temporary storage.

Topological Sort

As part of backprop, we need to sort the nodes of our graph so we can traverse the graph in the appropriate order.

Exercise - implement `topological_sort`

```yaml Difficulty: 🔴🔴🔴🔴⚪ Importance: 🔵⚪⚪⚪⚪

You should spend up to 20-25 minutes on this exercise. Note, it's completely fine to skip this problem if you're not very interested in it. It's more of a fun LeetCode-style challenge, and writing a solution for it isn't crucial for understanding today's content. ```

Write a general function topological_sort that return a list of node's children in topological order (beginning with the furthest descendants, ending with the starting node) using depth-first search.

We've given you a Node class, with a children attribute, and a get_children function. You shouldn't change any of these, and your topological_sort function should use get_children to access a node's children rather than calling node.children directly. In subsequent exercises, we'll replace the Node class with the Tensor class (and using a different get_children function), so this will ensure your code still works for this new case.

If you're stuck, try looking at the pseudocode from some of these examples.

class Node:
    def __init__(self, *children):
        self.children = list(children)


def get_children(node: Node) -> list[Node]:
    return node.children


def topological_sort(node: Node, get_children: Callable) -> list[Node]:
    """
    Return a list of node's descendants in reverse topological order from future
    to past (i.e. `node` should be last).

    Should raise an error if the graph with `node` as root is not in fact acyclic.
    """
    raise NotImplementedError()


tests.test_topological_sort_linked_list(topological_sort)
tests.test_topological_sort_branching(topological_sort)
tests.test_topological_sort_rejoining(topological_sort)
tests.test_topological_sort_cyclic(topological_sort)

Help - my function is hanging without returning any values.

This is probably because it's going around in cycles when fed a cyclic graph. You should add a way of raising an error if your function detects that the graph isn't cyclic. One way to do this is to create a set temp, which stores the nodes you've visited on a particular excursion into the graph, then you can raise an error if you come across an already visited node.

Help - I'm completely stuck on how to implement this, and would like the template for some code.

Here is the template for a depth-first search implementation:

def topological_sort(node: Node, get_children: Callable) -> list[Node]:
result: list[Node] = [] # stores the list of nodes to be returned (in reverse topological order)
    perm: set[Node] = set() # same as result, but as a set (faster to check for membership)
    temp: set[Node] = set() # keeps track of previously visited nodes (to detect cyclicity)
def visit(cur: Node):
        '''
        Recursive function which visits all the children of the current node, and appends them all
        to result in the order they were found.
        '''
        pass
visit(node)
    return result

Solution

def topological_sort(node: Node, get_children: Callable) -> list[Node]:
    """
    Return a list of node's descendants in reverse topological order from future
    to past (i.e. node should be last).
    Should raise an error if the graph with node as root is not in fact acyclic.
    """
    result: list[
        Node
    ] = []  # stores the list of nodes to be returned (in reverse topological order)
    perm: set[Node] = set()  # same as result, but as a set (faster to check for membership)
    temp: set[Node] = set()  # keeps track of previously visited nodes (to detect cyclicity)
def visit(cur: Node):
        """
        Recursive function which visits all the children of the current node,
        and appends them all to result in the order they were found.
        """
        if cur in perm:
            return
        if cur in temp:
            raise ValueError("Not a DAG!")
        temp.add(cur)
for next in get_children(cur):
            visit(next)
result.append(cur)
        perm.add(cur)
        temp.remove(cur)
visit(node)
    return result

Now, we've given you the function sorted_computational_graph. This calls topological_sort and returns the result in reverse order (because we want to start with the root node). The "get children" function we're using here is "return all tensors in the recipe for this tensor".

def sorted_computational_graph(tensor: Tensor) -> list[Tensor]:
    """
    For a given tensor, return a list of Tensors that make up the nodes of the given Tensor's
    computational graph, in reverse topological order (i.e. `tensor` should be first).
    """

    def get_parents(tensor: Tensor) -> list[Tensor]:
        if tensor.recipe is None:
            return []
        return list(tensor.recipe.parents.values())

    return topological_sort(tensor, get_parents)[::-1]


a = Tensor([1], requires_grad=True)
b = Tensor([2], requires_grad=True)
c = Tensor([3], requires_grad=True)
d = a * b
e = c.log()
f = d * e
g = f.log()
name_lookup = {a: "a", b: "b", c: "c", d: "d", e: "e", f: "f", g: "g"}

print([name_lookup[t] for t in sorted_computational_graph(g)])

['g', 'f', 'e', 'c', 'd', 'b', 'a']

Compare your output with the computational graph. You should never be printing x before y if there is an edge x --> ... --> y (this should result in approximately reverse alphabetical order).

The `backward` method

Now we're really ready for backprop!

Recall that in the implementation of the class Tensor, we had:

class Tensor:
    ...
    def backward(self, end_grad: "Arr | Tensor | None" = None) -> None:
        if isinstance(end_grad, Arr):
            end_grad = Tensor(end_grad)
        return backprop(self, end_grad)

In other words, for a tensor out, calling out.backward() is equivalent to backprop(out).

Recall that in the last section, we said that calling backward on a scalar tensor is equivalent to backpropagating on the weighted sum of all the elements of the tensor, i.e. L = (tensor * v).sum(). By default v is a tensor of 1s of the same shape as the tensor you're calling backward from, meaning we're just backpropagating on L.sum(). Here, the end_grad argument you pass to backward gives you the option to override this default behaviour, in other words if it's supplied you should use it as the first input to your backward function instead of a tensor of 1s. The use case for this is pretty niche (used for things like influence functions), but it's still useful to understand!

Exercise - implement `backprop`

```yaml Difficulty: 🔴🔴🔴🔴🔴 Importance: 🔵🔵🔵🔵🔵

You should spend up to 30-45 minutes on this exercise.

This exercise is the most conceptually important today, and probably the hardest. We've provided several dropdowns to help you. ```

Now, we get to the actual backprop function! Some code is provided below, which you should complete.

If you want a challenge, you can try and implement it straight away, with out any help. However, because this is quite a challenging exercise, you can also use the dropdowns below. The first one gives you a sketch of the backpropagation algorithm, the second gives you a diagram which provides a bit more detail, and the third gives you the annotations for the function (so you just have to fill in the code). You are recommended to start by trying to implement it without help, but use the dropdowns (in order) if this is too difficult.

We've also provided a few dropdowns to address specific technical errors that can arise from implementing this function. If you're having trouble, you can use these to help you debug. You should take some time with this function, as it's definitely the most important exercise to understand today.

def backprop(end_node: Tensor, end_grad: Tensor | None = None) -> None:
    """Accumulates gradients in the grad field of each leaf node.

    tensor.backward() is equivalent to backprop(tensor).

    end_node:
        The rightmost node in the computation graph. If it contains more than one element, end_grad
        must be provided.
    end_grad:
        A tensor of the same shape as end_node. Set to 1 if not specified and end_node has only one
        element.
    """
    # Get value of end_grad_arr
    end_grad_arr = np.ones_like(end_node.array) if end_grad is None else end_grad.array

    # Create dict to store gradients
    grads: dict[Tensor, Arr] = {end_node: end_grad_arr}

    # YOUR CODE HERE - iterate through the sorted computational graph, performing backprop algorithm
    raise NotImplementedError()


tests.test_backprop(Tensor)
tests.test_backprop_branching(Tensor)
tests.test_backprop_requires_grad_sum(Tensor)
tests.test_backprop_requires_grad_false(Tensor)
tests.test_backprop_float_arg(Tensor)

Help - I get AttributeError: 'NoneType' object has no attribute 'func'

This error is probably because you're trying to access recipe.func from the wrong node. Possibly, you're calling your backward functions using the parents nodes' recipe.func, rather than the node's recipe.func.

To explain further, suppose your computational graph is simply:

When you reach b in your backprop iteration, you should calculate the gradient wrt a (the only parent of b) and store it in your grads dictionary, as grads[a]. In order to do this, you need the backward function for func1, which is stored in the node b (recall that the recipe of a tensor can be thought of as a set of instructions for how that tensor was created).

Help - I get AttributeError: 'numpy.ndarray' object has no attribute 'array'

This might be because you've set node.grad to be an array, rather than a tensor. You should store gradients as tensors (think of PyTorch, where tensor.grad will have type torch.Tensor).

It's fine to store numpy arrays in the grads dictionary, but when it comes time to set a tensor's grad attribute, you should use a tensor.

Help - I get 'RuntimeError: bool value of Tensor with more than one value is ambiguous'.

This error is probably because your computational graph function checks whether a tensor is in a list. The way these classes are compared for equality is a bit funky, and using sets rather than lists should make this error go away (i.e. checking whether a tensor is in a set should be fine).

Help - I'm failing on the test_backprop_requires_grad_sum test and I don't know why.

This test is designed to spot cases where you're accidentally overwriting the gradient with each backward fn call, rather than summing them. Remember that if a node has multiple paths from itself to the end node, then that node's grad attribute should be the sum of the gradients from all those

Help - I'm stuck, and I need a template for the function.

You just need to fill in the code below the comments labelled (1) and (2).

def backprop(end_node: Tensor, end_grad: Tensor | None = None) -> None:
# Get value of end_grad_arr
    end_grad_arr = np.ones_like(end_node.array) if end_grad is None else end_grad.array
# Create dict to store gradients
    grads: dict[Tensor, Arr] = {end_node: end_grad_arr}
for node in sorted_computational_graph(end_node):
        outgrad = grads.pop(node)
# (1) If this is a leaf node, then set/update the gradient if requires_grad
        ...
# (2) If this isn't a leaf node, then iterate through this node's parents and update their values in the grads
        # dict, using the outgrad values returned from this node's backward function
        ...

Solution

def backprop(end_node: Tensor, end_grad: Tensor | None = None) -> None:
    """Accumulates gradients in the grad field of each leaf node.
    tensor.backward() is equivalent to backprop(tensor).
    end_node:
        The rightmost node in the computation graph. If it contains more than one element, end_grad
        must be provided.
    end_grad:
        A tensor of the same shape as end_node. Set to 1 if not specified and end_node has only one
        element.
    """
    # Get value of end_grad_arr
    end_grad_arr = np.ones_like(end_node.array) if end_grad is None else end_grad.array
# Create dict to store gradients
    grads: dict[Tensor, Arr] = {end_node: end_grad_arr}
for node in sorted_computational_graph(end_node):
        # Get the outgrad from the grads dict
        outgrad = grads.pop(node)
# (1) If it's a leaf node, then set/update gradient if requires_grad=True, and stop here.
        if node.is_leaf:
            if node.requires_grad:
                node.grad = Tensor(outgrad) if node.grad is None else node.grad + outgrad
# (2) If not a leaf node then it must have a recipe, so we iterate through its parents and
        # update their grads.
        else:
            for argnum, parent in node.recipe.parents.items():
                # Get backward function, from the fwd function that created node from parent.
                back_fn = BACK_FUNCS.get_back_func(node.recipe.func, argnum)
# Use it to compute the gradient we'll add onto parent from the path parent -> node
                # -> ... -> end_node.
                in_grad = back_fn(outgrad, node.array, *node.recipe.args, **node.recipe.kwargs)
# Add this gradient to the grads dict (handling special case where parent is not in
                # grads yet).
                grads[parent] = in_grad if (parent not in grads) else grads[parent] + in_grad

2️⃣ Autograd

Learning Objectives

Wrapping Arrays (Tensor)

Recipe

Registering backwards functions

Exercise - implement BackwardFuncLookup

Tensors

requires_grad and is_leaf

Forward Pass: Building the Computational Graph

Exercise - implement log_forward

Exercise - implement multiply_forward

Forward Pass - Generic Version

Exercise - implement wrap_forward_fn

Backpropagation

Topological Sort

Exercise - implement topological_sort

The backward method

Exercise - implement backprop

Exercise - implement `BackwardFuncLookup`

`requires_grad` and `is_leaf`

Exercise - implement `log_forward`

Exercise - implement `multiply_forward`

Exercise - implement `wrap_forward_fn`

Exercise - implement `topological_sort`

The `backward` method

Exercise - implement `backprop`