1️⃣ Rays & Segments

Learning Objectives

• Learn how to create PyTorch tensors in a variety of ways
• Understand how to parametrize lines and rays in 2D
• Learn about type annotations and linear operations in PyTorch

1D Image Rendering

In our initial setup, the camera will be a single point at the origin, and the screen will be the plane at x=1.

Objects in the world consist of triangles, where triangles are represented as 3 points in 3D space (so 9 floating point values per triangle). You can build any shape out of sufficiently many triangles and your Pikachu will be made from 412 triangles.

The camera will emit one or more rays, where a ray is represented by an origin point and a direction point. Conceptually, the ray is emitted from the origin and continues in the given direction until it intersects an object.

We have no concept of lighting or color yet, so for now we'll say that a pixel on our screen should show a bright color if a ray from the origin through it intersects an object, otherwise our screen should be dark.

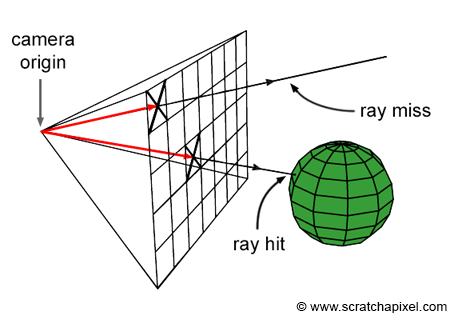
To start, we'll let the z dimension in our (x, y, z) space be zero and work in the remaining two dimensions.

Exercise - implement make_rays_1d

```yaml Difficulty: 🔴🔴⚪⚪⚪ Importance: 🔵🔵🔵⚪⚪

You should spend up to 10-15 minutes on this exercise. ```

Implement the following make_rays_1d function so it generates some rays coming out of the origin, which we'll take to be (0, 0, 0).

Calling render_lines_with_plotly on your rays will display them in a 3D plot.

def make_rays_1d(num_pixels: int, y_limit: float) -> Tensor:
    """
    num_pixels: The number of pixels in the y dimension. Since there is one ray per pixel, this is
        also the number of rays.
    y_limit: At x=1, the rays should extend from -y_limit to +y_limit, inclusive of both endpoints.

    Returns: shape (num_pixels, num_points=2, num_dim=3) where the num_points dimension contains
        (origin, direction) and the num_dim dimension contains xyz.

    Example of make_rays_1d(9, 1.0): [
        [[0, 0, 0], [1, -1.0, 0]],
        [[0, 0, 0], [1, -0.75, 0]],
        [[0, 0, 0], [1, -0.5, 0]],
        ...
        [[0, 0, 0], [1, 0.75, 0]],
        [[0, 0, 0], [1, 1, 0]],
    ]
    """
    raise NotImplementedError()


rays1d = make_rays_1d(9, 10.0)
fig = render_lines_with_plotly(rays1d)

def make_rays_1d(num_pixels: int, y_limit: float) -> Tensor:
    """
    num_pixels: The number of pixels in the y dimension. Since there is one ray per pixel, this is
        also the number of rays.
    y_limit: At x=1, the rays should extend from -y_limit to +y_limit, inclusive of both endpoints.
    Returns: shape (num_pixels, num_points=2, num_dim=3) where the num_points dimension contains
        (origin, direction) and the num_dim dimension contains xyz.
    Example of make_rays_1d(9, 1.0): [
        [[0, 0, 0], [1, -1.0, 0]],
        [[0, 0, 0], [1, -0.75, 0]],
        [[0, 0, 0], [1, -0.5, 0]],
        ...
        [[0, 0, 0], [1, 0.75, 0]],
        [[0, 0, 0], [1, 1, 0]],
    ]
    """
    rays = t.zeros((num_pixels, 2, 3), dtype=t.float32)
    t.linspace(-y_limit, y_limit, num_pixels, out=rays[:, 1, 1])
    rays[:, 1, 0] = 1
    return rays

Tip - the out keyword argument

Many PyTorch functions take an optional keyword argument out. If provided, instead of allocating a new tensor and returning that, the output is written directly to the out tensor.

If you used torch.arange or torch.linspace above, try using the out argument. Note that a basic indexing expression like rays[:, 1, 1] returns a view that shares storage with rays, so writing to the view will modify rays. You'll learn more about views later today.

Ray-Object Intersection

Suppose we have a line segment defined by points $L_1$ and $L_2$. Then for a given ray, we can test if the ray intersects the line segment like so:

• Supposing both the ray and line segment were infinitely long, solve for their intersection point.
• If the point exists, check whether that point is inside the line segment and the ray.

Our camera ray is defined by the origin $O$ and direction $D$ and our object line is defined by points $L_1$ and $L_2$.

We can write the equations for all points on the camera ray as $R(u)=O +u D$ for $u \in [0, \infty)$ and on the object line as $O(v)=L_1+v(L_2 - L_1)$ for $v \in [0, 1]$.

The following interactive widget lets you play with this parameterization of the problem. Run the cells one after another:

fig: go.FigureWidget = setup_widget_fig_ray()
display(fig)


@interact(v=(0.0, 6.0, 0.01), seed=(0,10,1))
def update(v=0.0, seed=0):
    t.manual_seed(seed)
    L_1, L_2 = t.rand(2, 2)
    P = lambda v: L_1 + v * (L_2 - L_1)
    x, y = zip(P(0), P(6))
    with fig.batch_update():
        fig.update_traces({"x": x, "y": y}, 0)
        fig.update_traces({"x": [L_1[0], L_2[0]], "y": [L_1[1], L_2[1]]}, 1)
        fig.update_traces({"x": [P(v)[0]], "y": [P(v)[1]]}, 2)

Setting the line equations from above equal gives the solution:

Once we've found values of $u$ and $v$ which satisfy this equation, if any (the lines could be parallel) we just need to check that $u \geq 0$ and $v \in [0, 1]$.

Exercise - implement intersect_ray_1d

```yaml Difficulty: 🔴🔴🔴⚪⚪ Importance: 🔵🔵🔵🔵⚪

You should spend up to 20-25 minutes on this exercise. It involves some of today's core concepts - tensor manipulation, linear operations, etc. ```

Using torch.linalg.solve and torch.stack, implement the intersect_ray_1d function to solve the above matrix equation.

>>> t.stack([t.ones(2, 2), t.zeros(2, 2)], dim=0)
tensor([[[1., 1.],
         [1., 1.]],
[[0., 0.],
         [0., 0.]]])

>>> t.cat([t.ones(2, 2), t.zeros(2, 2)], dim=0)
tensor([[1., 1.],
        [1., 1.],
        [0., 0.],
        [0., 0.]])

Is it possible for the solve method to fail? Give a sample input where this would happen.

def intersect_ray_1d(
    ray: Float[Tensor, "points dims"], segment: Float[Tensor, "points dims"]
) -> bool:
    """
    ray: shape (n_points=2, n_dim=3)  # O, D points
    segment: shape (n_points=2, n_dim=3)  # L_1, L_2 points

    Return True if the ray intersects the segment.
    """
    raise NotImplementedError()


tests.test_intersect_ray_1d(intersect_ray_1d)
tests.test_intersect_ray_1d_special_case(intersect_ray_1d)

def intersect_ray_1d(
    ray: Float[Tensor, "points dims"], segment: Float[Tensor, "points dims"]
) -> bool:
    """
    ray: shape (n_points=2, n_dim=3)  # O, D points
    segment: shape (n_points=2, n_dim=3)  # L_1, L_2 points
    Return True if the ray intersects the segment.
    """
    # Get the x and y coordinates (ignore z)
    ray = ray[:, :2]
    segment = segment[:, :2]
# Ray is [[Ox, Oy], [Dx, Dy]]
    O, D = ray
    # Segment is [[L1x, L1y], [L2x, L2y]]
    L_1, L_2 = segment
# Create matrix and vector, and solve equation
    mat = t.stack([D, L_1 - L_2], dim=-1)
    vec = L_1 - O
# Solve equation (return False if no solution)
    try:
        sol = t.linalg.solve(mat, vec)
    except RuntimeError:
        return False
# If there is a solution, check the soln is in the correct range for there to be an intersection
    u = sol[0].item()
    v = sol[1].item()
    return (u >= 0.0) and (v >= 0.0) and (v <= 1.0)

Aside - type hints

Adding type hints to your code is a useful habit to get into. Some advantages of using them:

• They help document your code, making it more readable (for yourself and for others)
• The improve IDE behaviour, i.e. getting better code completion
• They encourage better code structure, since they force you to consider your inputs & outputs explicitly
• They make debugging easier, since you'll find it easier to spot where a variable might not match the type signature you've given for it

As well as simple objects, you can also typecheck iterables of objects, for example:

• list[int] for a list of integers,
• dict[str, float] for a dict mapping strings to floats,
• tuple[Tensor, Tensor] for a length-2 tuple containing tensors,
• tuple[int, ...] for a tuple containing one or more integers.

and you can also use other syntax to extend behaviour, e.g. x: int | None for a variable which can either be an integer or None.

Jaxtyping also gives us useful type hint features, e.g. we have ray: Float[Tensor, "points dims"] to indicate a tensor of floats with dimensions points and dims. Unlike the examples above this is unlikely to be captured by syntax highlighting when you make a mistake, instead it's best to view this as an alternative to annotating the tensor shape. You may or may not prefer to use this.

When in doubt however, it's best to make assertions on the variable type or tensor shape explicitly, e.g. assert isinstance(x, Tensor) or assert x.shape == .... We generally don't recommend static type checking like mypy in this course, because there aren't generally standard and robust ways to do it which will fit all IDEs & use-cases.